Свойства сходящихся рядов

· Если сходится ряд: 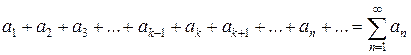, то сходится и ряд: 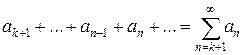, и обратно, если сходится ряд: 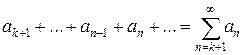, то сходится и ряд: 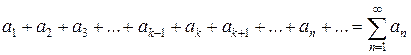. Другими словами на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов.

Установлено, что сходящиеся ряды можно умножать на число, почленно складывать и вычитать так же, как и конечные суммы:

· Если сходится ряд: 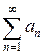и его сумма равна S, то и ряд 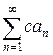где С=const, сходится и его сумма равна cS.

· Если сходятся ряды: 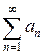и и их суммы равны S_а и S_b, то и ряд , сходится и его сумма равна S_а±S_b.

Необходимое условие сходимости ряда:

Если ряд 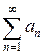сходится, то его общий член стремится к нулю, то есть 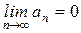. Данное условие не является достаточным.

Рассмотрим гармонический ряд: и он расходится.

Достаточные признаки сходимости положительных рядов

Необходимое и достаточное условие сходимости положительного ряда:Для того чтобы ряд 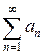с неотрицательными членами сходился необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.

Признаки сравнения:

· (сходимости) - Пусть даны два ряда с неотрицательными членами 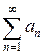и и для всех n выполняется неравенство . Тогда если ряд сходится, то ряд 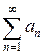тоже сходится;

· (расходимости) - Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство 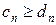. Тогда если ряд расходится, то ряд тоже расходится.

Признак Даламбера: Пусть дан ряд с положительными членами 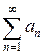и существует .

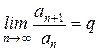· если q<1 – ряд сходится;

· если q>1 – ряд расходится;

· если q=1 – ряд может и сходиться и расходиться, то есть данный признак неприменим.

Признак Коши: Пусть дан ряд с положительными членами 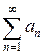и существует .

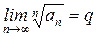· если q<1 – ряд сходится;

· если q>1 – ряд расходится;

· если q=1 – ряд может и сходиться и расходиться, то есть данный признак неприменим.

Интегральный признак: Пусть дан ряд с положительными членами, являющимися значениями некоторой функции f(x), непрерывной и убывающей на полуинтервале [1; +¥). Тогда ряд 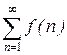будет сходиться в том случае, если сходится несобственный интеграл: 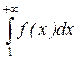и расходиться в случае его расходимости.

Обобщённый гармонический ряд: :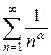

· сходится при a>1;

· расходится при 0<a£1.

Знакопеременный ряд. Признак Лейбница

Ряд называется знакопеременным, если его члены поочерёдно положительны и отрицательны: , где а_n>0.

Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться два условия:

1) ;

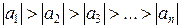2) .

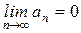Замечание: остаток такого ряда имеет тот же знак, что и первый отбрасываемый член, и меньше его по абсолютному значению.