Задачи для контрольных заданий

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Камский институт инженерных и гуманитарных технологий

АВЕРЬЯНОВ В.Е., ПОРЦЕВА Л.И., БАРАНОВА Н.А.

МАТЕМАТИКА

УЧЕБНО-ПРАКТИЧЕСКОЕ ПОСОБИЕ

Задания контрольной работы

ИЖЕВСК 2005

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ.

При выполнении и оформлении контрольных работ необходимо соблюдать

следующие правила:

1) контрольная работа выполняется в отдельной тетради, а не на листках, обязательно чернилами или шариковой ручкой (цвет чернил или пасты – любой, кроме красного) с полями шириной 4-5 см для замечаний рецензента;

2) на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы и дата отсылки работы в институт;

3) в работу должны быть включены все задания. Задачи и их решения располагаются в порядке возрастания номеров, перед решением задачи должен быть записан ее номер и ее условие. Условие задачи переписывается полностью, без сокращения слов.

4) решение задачи должно начинаться со слова “Решение”. Само решение должно представлять собой связный текст, а не голый набор формул и преобразований, причем пояснительный текст должен быть минимально необходимым. Окончательный результат решения задачи необходимо выделить с предшествующим ему словом “Ответ”.

4) Если в работе имеются ошибки, студент должен выполнить все требования преподавателя, изложенные в рецензии, и отправить работу с исправлениями на повторную проверку. Поэтому рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для их исправления и дополнения.

5) Никакие исправления в тексте уже проверенной работы не допускаются. Все исправления записываются после рецензии преподавателя с указанием номера задачи, к которой они относятся.

6) В случае незачета работы и отсутствия прямого указания рецензента на то, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново.

Контрольные работы, выполненные с нарушением изложенных требований или выполненные студентами не по своему варианту, не засчитываются и возвращаются без проверки.

Контрольные работы должны выполнятся самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала; в результате чего студент не приобретает необходимых знаний и может оказаться неподготовленным к устному зачету и экзамену.

Каждую контрольную работу после проверки студент предъявляет к защите.

На защите студент должен объяснить и, в случае необходимости, защитить свое решение, ответить на поставленные преподавателем вопросы по решенным в работе задачам. Без предъявления защищенных работ студент не допускается к сдаче зачета и экзамена.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Основная

1. Аверьянов В.Е., Никулин В.А., Понамарев В.А. Математика: Учеб. Пособие / Под ред. В.А. Никулина.- Ижевск, КИГИТ, 2004.
2. Баврин И.И., Матросов В.Л. Общий курс высшей математики. – М.: Просвещение, 1995.
3. Данко П.Е.,Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Учебное пособие для вузов – М.: Высшая школа, 1999.
4. Шипачев В.С. Высшая математика. Учебник для вузов. - М.:Высшая школа,2003.

Дополнительная

1. Бронштейн И.Н., Семендяев К.А. Справочник по математики для инженеров и учащихся втузов. М.: Наука, 1980.
2. Высшая математика для экономистов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. – М.: ЮНИТИ, 2000.
3. Беклкмемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1976.
4. Никольский С.М. Курс математического анализа. – М.: Наука, 1983. – Т.1.
5. Баврин И.И. Курс Высшей математики. – М.: Просвещение, 1992.

Пример 1.

Дана система трех линейных уравнений с тремя неизвестными. Доказать ее совместност ь и решить тремя способами: 1) с помощью формул Крамера; 2) методом матричного исчисления; 3) методом Гаусса.

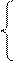1) x₁ - 5х₂ + 2х₃ = 6

3x₁ - х₂ - х₃ = - 3

-2x₁ + 2х₂ + 3х₃ = 3

Решение .Вычислим определитель системы.

∆= =1∙(-1)∙3 + (-5)∙(-1)∙(-2) + 2∙3∙2 - 2∙(-1)∙(-2) – (-5)∙3∙3 - 1∙(-1)∙2=42.

Так как ∆≠0, то система совместна и имеет единственное решение.

Найдем ∆₁, ∆₂,∆₃, - определители третьего порядка, полученные из определителя системы ∆ заменой 1, 2 и 3-го столбца соответственно столбцом свободных членов.

∆₁ = 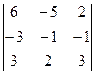= - 42, ∆₂ = 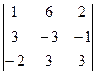= -42, ,∆₃ = 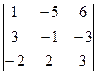= 42.

Подставляя найденные значения определителей в формулы Крамера, получаем искомое решение системы: х₁=∆₁/∆=-1, х₂= ∆₂/∆=-1, х₃= ∆₃/∆= 1.

Сделаем проверку.

-1 - 5∙ (-1) + 2∙1 = 6 - верно,

3∙(-1) – (-1) – 1 = -3 - верно,

-2∙(-1) + 2∙(-1) + 3∙1 = 3 - верно.

Ответ: х₁=-1, х₂= -1, х₃= 1.

2) Решим систему методом Гаусса.

x₁ - 5х₂ + 2х₃ = 6

3x₁ - х₂ - х₃= - 3

-2x₁ + 2х₂ + 3х₃ = 3

Расширенная матрица системы имеет вид . Преобразуем расширенную матрицу системы следующим образом.

Шаг 1. 1-ю строку умножая на (- 3), 2 и прибавляя полученные строки соответственно ко второй, третьей строкам, исключим переменную x₁из второй и третьей строк .

Шаг 2. 2-ю строку умножая на 4 и прибавяя к 3-ей, исключим из нее переменную х₂.

Таким образом , имеем:

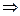
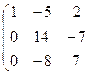
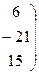
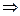
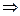
Используя обратный ход метода Гаусса найдем

из 3-го уравнения : 3х₃ = 3 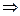х₃ = 1

из 2 -го уравнения : 2х₂ - х₃ = -3 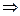2х₂ - 1 = -3 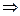х₂ = -1

из 1 -го уравнения : x₁ - 5х₂ + 2х₃ = 6 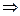x₁ + 5 + 2 = 6 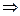x₁ = -1

Ответ: х₁=-1, х₂= -1, х₃= 1.

3). Решим систему уравнений матричным методом. Здесь

A = ; Х= ; В= .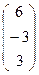

Так как определитель матрицы системы отличен от нуля: |A| = 42 , то матрица А имеет обратную. Для нахождения обратной матрицы А^-1 вычислим алгебраические дополнения элементов матрицы А и составим матрицу из алгебраических дополнений

||A_{i j}|| = .Транспонируем матрицу из алгебраических дополнений ||A_{i j} ||^T = 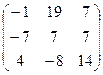.Разделив каждый элемент транспонированной матрицы на определитель, получим обратную матрицу А^-1=1/42 .

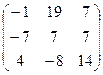Умножив слева обратную матрицу на матрицу столбец свободных членов, получим искомую матрицу столбец неизвестных: Х=А^-1∙В или

Х= = 1/42 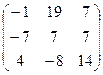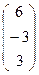= 1/42 = .

Ответ: х₁=-1, х₂= -1, х₃= 1.

Пример 2.Даны вершины А₁(3; -2; 2), А₂(1; -3; 1), А₃(2; 0; 4),А₄(6; -4: 6). Средствами векторной алгебры найти:

1) длину ребра А₁ А₂

2) угол между ребрами А₁ А₂и А₁ А₃

3) площадь грани А₁А₂А₃

4) объем пирамиды А₁А₂А₃А₄

Решение. 1) Находим вектор А₁А₂:

=(1 - 3)i+ (-3 – (-2))j +(1 – 2)k= - 2i - 1j - k.

Длину вектора, т.е. длину ребра А₁А₂ найдем по формуле

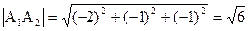
2) Найдем координаты вектора =(2 – 3)i +(0 –(- 2))j +(4 -2)k= - i + 2j + 2k.

Скалярное произведение векторов и находим по формуле

∙ =(-2) ∙ (-1) + (-1) ∙ 2 + (-1) ∙ 2 = - 2, а косинус угла между ними – по формуле: .

Отсюда следует, что φ – тупой угол, φ=π – arccos0,27 = 1,85 рад с точностью до 0,01. Это и есть искомый угол между ребрами А₁ А₂ и А₁ А₃ .

3) Площадь грани А₁А₂А₃равна половине площади параллелограмма, построенного на векторах и , т.е. половине модуля векторного произведения этих векторов:

x = .

Здесь определитель вычисляется с помощью разложения по первой строке. Следовательно,

.

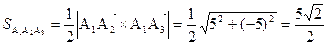4) Объем Vпирамиды равен 1/6 объема параллелепипеда, построенного на векторах

, и 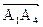. Вектор 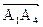=3 i - 2j + 4k. Используя формулу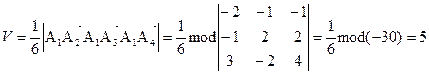

.

Пример. Найти центры и привести к каноническому виду и построить кривые :

1) 2 x² + 3 y² - 4x + 6y - 7 = 0 ;

2) 2 x y = a²

Решение1). B = 0, = -72 0 , 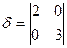= 6 > 0 - эллипс

Выполним приведение к полному квадрату: 2 (x - 1)² + 3 (y + 1)² - 12 = 0

Координаты центра симметрии ( 1; - 1), линейное преобразование X = x - 1, Y = y + 1 приводит уравнение к каноническому виду X² /6 + Y² /4 = 1 , где a = 2.48 ,b = 2

2). B = 1, 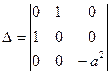= a² 0 , = - 1 < 0 - гипербола

Центр системы координат находится в центре симметрии кривой, т.к. в уравнении нет линейных членов. Совершим поворот осей на угол .. По формуле ( 45 ) имеем tg 2 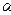= B/(A - C) = 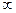, т.е. 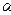= 45⁰. Коэффициенты канонического уравнения ( 46 ) A⁺ , C⁺ определяются уравнением ( 48 ) : t² = 1 или t_1,2 = 1 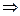A⁺ = 1, C⁺ = -1, т.е. X² - Y² = a² или X² / a² - Y² / a² = 1

Уравнение 2х у = а² описывает гиперболу с центром в (0;0). Оси симметрии располагаются по биссектрисам координатных углов, асимптотами служат оси координат, полуоси гиперболы равны а.

Задачи для контрольных заданий

Контрольная работа №1

ЗАДАНИЕ 1

Дана система трех линейных уравнений с тремя неизвестными. Доказать ее совместность и решить тремя способами: 1) с помощью формул Крамера; 2) методом матричного исчисления; 3) методом Гаусса.

2х₁ + х₂ + 3х₃ = 7

1.1 2х₁ + 3х₂ + х₃ = 1

3х₁ + 2х₂ + х₃ = 6

2х₁ - х₂ + 2х₃ = 3

1.2 х₁ + х₂ + 2х₃ = -4

4х₁ + х₂ + 4х₃ = -3

3х₁ - х₂ + х₃ = 12

1.3 х₁ + 2х₂ + 4х₃= 6

5х₁ + х₂ + 2х₃ = 3

2х₁ - х₂ + 3х₃ = -4

1.4 х₁ + 3х₂ - х₃ = 11

х₁ - 2х₂ + 2х₃ = -7

3х₁ - 2х₂ + 4х₃ = 12

1.5 3х₁ + 4х₂ - 2х₃ = 6

2х₁ - х₂ - х₃ = -9

8х₁ + 3х₂ - 6х₃ = -4

1.6 х₁ + х₂ - х₃ = 2

4х₁ + х₂ - 3х₃ = -5

4х₁ + х₂ - 3х₃ = 9

1.7 х₁ + х₂ - х₃ = -2

8х₁ + 3х₂ - 6х₃ = 12

2х₁ + 3х₂ + 4х₃ = 33 1.8 7х₁ - 5х₂ = 24

4х₁ + 11х₃ = 39

2х₁ + 3х₂ + 4х₃ = 12

1.9 7х₁ - 5х₂ + х₃ = -33

4х₁ + х₃ = -7

х₁ + 4х₂ - х₃ = 6

1.10 5х₂ + 4х₃ = -20

3х₁ - 2х₂ + 5х₃ = -22

ЗАДАНИЕ 2

Даны вершины А(Х₁;Y₁), В(Х₂;Y₂), С(Х₃;Y₃) треугольника АВС. Требуется найти:

а) уравнение стороны АВ ;

б) уравнение высоты СН;

в) уравнение медианы АМ;

г) Точку пересечения Р медианы АМ и высоты СН;

д) расстояние от точки С до прямой АВ;

е) величина (в радианах) внутреннего угла А;

ж) площадь треугольника АВС.

2.1 А(-2;4), В(3;1), С(10;7).

2.2А(-3;-2), В(14;4), С(6;8).

2.3А(1;7), В(-3;-1), С(11;-3).

2.4А(1;0), В(-1;4), С(9;5).

2.5А(1;-2), В(7;1), С(3;7).

2.6А(-2;-3), В(1;6), С(6;1).

2.7А(-4;2), В(-6;6), С(6;2).

2.8 А(4;-3), В(7;3), С(1;10).

2.9 А(4;-4), В(8;2), С(3;8).

2.10А(-3;-3), В(5;-7), С(7;7).

ЗАДАНИЕ 3

3.1.Составить уравнение линии, расстояние каждой точки которой от точки А(2;-2) вдвое меньше, чем от прямой Х+1=0.

3.2. Составить уравнение линии, расстояние каждой точки которой от точки А(2;-2) вдвое больше, чем от прямой Х+1=0.

3.3. Составить уравнение линии, каждая точка которой равноудалена от точки А(3;1) и от прямой Y+5=0.

3.4.Составить уравнение линии, расстояние каждой точки которой от точки А(3;4) в два раза больше, чем от точки В(6;7).

3.5.Составить уравнение геометрического места точек, являющихся центрами окружностей, проходящих через точку А(3;2) и касающихся оси ОХ.

3.6.Составить уравнение геометрического места центров окружностей, проходящих через точку А(-4;2) и касающихся оси OY.

3.7.Составит уравнение линии, сумма расстояния точек которой от точек А(2;4) и В(-4;4) равна 8.

3.8.Составить уравнение линии, сумма расстояния точек которой от точек А(2;-2) и В(2;4) равна 8.

3.9.Составить уравнение линии, каждая точка которой вдвое ближе к точке А(-4;3), чем к точке В(1;-2).

3.10.Составить уравнение линии, каждая точка которой равноудалена от прямой Х+6=0 и от начала координат.

ЗАДАНИЕ 4

Даны вершины А₁(X₁; Y₁; Z₁), А₂(X₂; Y₂; Z₂), А₃(X₃; Y₃; Z₃),

А₄(X₄; Y₄; Z₄). Средствами векторной алгебры найти:

а) длину ребра А₁ А₂

б) угол между ребрами А₁ А₂и А₁ А₃

в) площадь грани А₁А₂А₃

г) длину высоты пирамиды, проведенной из вершины А₄

д) уравнение высоты пирамиды, проведенной из вершины А₄

е) объем пирамиды А₁А₂А₃А₄

4.1. А₁(7;0;3), А₂(3;0;-1), А₃(3;0;5), А₄(4;3;-2).

4.2. А₁(1;-1;6), А₂(2;5;-2), А₃(-3;3;3), А₄(4;1;5).

4.3. А₁(3;6;1), А₂(6;1;4), А₃(3;-6;10), А₄(7;5;4).

4.4. А₁(1;1;3), А₂(6;1;4), А₃(6;4;1), А₄(0;5;6).

4.5. А₁(4;4;5), А₂(10;2;3), А₃(-3;5;4), А₄(6;-2;2).

4.6. А₁(-1;2;5), А₂(-4;6;4), А₃(2;1;5), А₄(-1;-2;2).

4.7. А₁(2;-1;9), А₂(1;1;5), А₃(7;3;1), А₄(2;6;-2).

4.8. А₁(1;-2;2), А₂(-1;-3;4), А₃(5;5;-1), А₄(2;-4;5).

4.9. А₁(1;1;3), А₂(7;1;1), А₃(2;2;2), А₄(4;1;-1).

4.10. А₁(3;1;2), А₂(5;0;-1), А₃(0;3;6), А₄(3;7;10).

ЗАДАНИЕ 5

Выяснить вид кривой по общему уравнению, найти ее параметры и положение в системе координат. Сделать рисунок.

5.1 х² + у² +6х – 4у – 68 = 0

5.2 9 х² - 4у² - 18х – 16у - 43 = 0

5.3 4х² + 5у² + 8х – 100у + 484 = 0

5.4 3х² - 6у² - 12х – 108у - 492 = 0

5.5 2х² + 9у² + 12х – 108у +324= 0

5.6 3х² - 10у² - 24 х – 100у - 172 = 0

5.7 4х² + 9у² + 32х – 72у + 172 = 0

5.8 5х² - 8у² - 50 х – 48у + 13= 0

5.9 6х² + 7у² + 60х – 28у + 136= 0

5.10 7х² - 6у² - 84х – 12у - 288=