Формулы преобразования координат. Поворотные матрицы
Для любой точки М тела с координатами x, y, z в подвижной системе координат Оxyz, жестко связанной с ним, и с ее же координатами X, Y, Z в неподвижной системе координат ОXYZ в соответствии с (3.10), взаимосвязь проекций вектора точки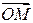 
на оси двух систем координат [X]н и [x]п имеет вид
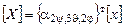, (3.14)
или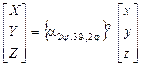 
, (3.15)
где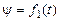 
,
,
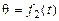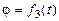-углы Эйлера; 
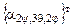- матрица, транспонированная к матрице направляющих косинусов 
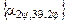,задающей преобразование поворота от осей неподвижной системы OXYZ (с базисом [X]н)к осям подвижной системы Оxyz (с базисом [x]п ), неизменно связанной с телом. Транспонированная матрица 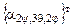получается путем замены в матрице 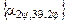строк на столбцы. Выражение 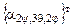находим из формул преобразований координат при переходе от одной системы к другой: [X]н® [x1] ®[x2]®[x]п, из которых две системы [x1] и [x2] промежуточные.
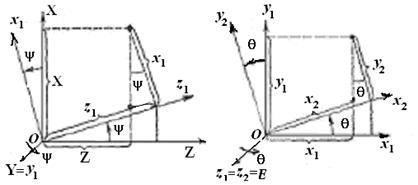
Переход от осей системы[X]н к осям системы [x1] осуществляется поворотом на угол прецессии ψвокруг неподвижной OY – оси прецессии системы [X]н (рис. 3.9 … 3.11).
Переход от осей системы[x1] к осям системы[x2] осуществляется поворотом на уголнутацииθ вокруг оси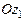 
системы [x1] (рис. 3.5 … 3.11,б).
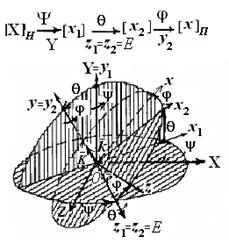
Рис. 3.9
Переход от осей системы [x2] к осям системы[x]п– поворотом на уголротации (собственного вращения ) φвокруг оси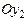 
системы[x2] .
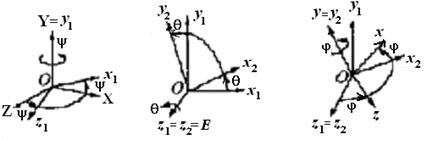
а б в
Рис. 3.10
Формулы преобразования координат получаем, рассмотрев переход от системы ОXYZ ([X]н) к системе Оxyz ([x]п), выполненный с помощью трех поворотов:
1. Поворота системы ОXYZ вокруг второй из координатных осей ОY на угол прецессии ψ, т.е. [X]н®[x1], ОXYZ ®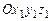 
, причем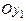 
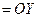(рис. 3.9 … 3.11,а). Координаты систем координат ОXYZ и 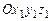(рис. 3.11,a) связаны соотношениями
X = x1 cos y + 0 + z1 sin y ,
Y = 0 + y1 + 0 ,
Z = - x1 sin y + 0 + z1 cos y ,
или в матричной форме
[X] ={a2y} т [x1], (3.16)
где поворотная матрица {a2y} т =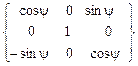 
(3.17)
описывает поворот вокруг второй оси ОY на угол прецессии ψ .
а б
Рис. 3.11
2. Поворота системы 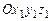вокруг третьей из коорди-натных осей 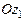на уголнутацииθ, т.е. [x1] ®[x2],
® 
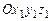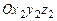, при этом = 
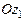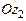(рис. 3.7,3.9, 3.11,б).
Формулы преобразования координат, как видно из рис. 3.11,б, при этом таковы:
x1 = x2 cos q - y2 sin q + 0,
y1 = x2 sin q + y2 cos q + 0,
z1 = 0 + 0 + z 2,
или в матричной форме
[x1] = {a3q } т [x2], (3.18)
где матрица {a3q } т =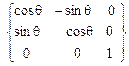 
(3.19)
описывает поворот вокруг оси 0z1 на угол нутации q.
3. Поворота системы 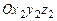вокруг второй из координатных осей 
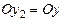на уголротации (собственного вращения ) φ,т.е.[x2]®[x]п(рис. 3.7, 3.9 … 3.11,а), 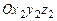® Cxyz,поэтому формулы преобразования координат, как видно из рис. 3.11,а, имеют вид
x(2) = x cos j + 0 + z sin j ,
y(2) = 0 + y + 0 ,
z(2) = - x sin j + 0 + z cos j ,
или в матричной форме
[x2 ] = { a2j }т [x], (3.20)
поворотная матрица { a2j }т аналогична (3.17) {a2y} т:
{a2φ} т =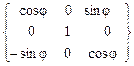 
. (3.21)
Подставляя в (3.16) соотношение (3.18), получаем промежуточную формулу преобразования координат, которая может понадобиться в дальнейшем
[X] ={a2y} т {a3q} т [x(2)] , (3.22)
где промежуточная поворотная матрица {a2y,3q }т находится как произведение двух матриц поворота,
{ a2y,3q }т = { a2y}т {a3q } т =
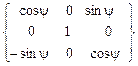
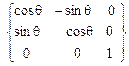= = (3.23)
= 
.
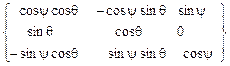Подставим в (3.16) формулы (3.18) и (3.20):
[X] ={a2y} т {a3q} т {a2j }т [x]. (3.24)
Сравнивая выражения (3.15) и (3.24), находим, что искомая поворотная матрица 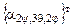является произведением трех матриц поворота (3.17), (3.19), (3.21):
{ay,q,j } т = 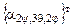= { a2y} т { a3q } т { a2j } т =
= 
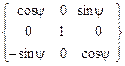
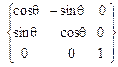
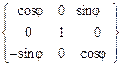=(3.25)
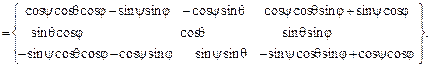
При заданном законе сферического движения выражения (3.15) и (3.25) позволяют определить искомый закон движения и траекторию выбранной точки твердого тела.