Метод эквивалентного генератора

Метод применяют в том случае, если необходимо определить ток в одной ветви разветвлённой схемы.

Идея метода.

1. Выделяется ветвь с сопротивлением, в которой необходимо определить ток 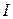. Остальную часть схемы представляют в виде активного двухполюсника, представленного на рисунке 2.43 а.

2. Активный двухполюсник заменяют эквивалентным источником питания (генератором). В результате получим простую одноконтурную схему, представленную на рисунке 2.43 б. Ток в полученой схеме равен

,

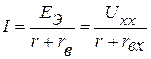где 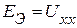- напряжению холостого хода активного двухполюсника (рис. 2.43 в),

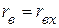– входное сопротивление пассивного двухполюсника.

Внутреннее сопротивление источника 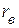равно входному сопротивлению пассивного двухполюсника 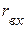, полученного из активного двухполюсника, путём изъятия из схемы источников питания и замены их внутренними сопротивлениями (рис. 2.43,г).

Рисунок 2.43 – Идея метода эквивалентного генератора

Рассмотрим справедливость вышеуказанного.

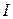1. В исходной схеме выделяем ветвь с сопротивлением , в которой необходимо определить ток . Остальную часть схемы представляем в виде активного двухполюсника 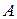(рис. 2.44 а).

Рисунок 2.44 – Доказательство метода эквивалентного генератора

2. Осуществляем разрыв выделенной ветви (рис. 2.44 б). В полученной схеме ток 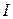равен нулю. Напряжение на зажимах равно напряжению холостого хода .

3. В разрыв включаем источник напряжения , величина которого равна напряжению холостого хода . (рис. 2.44 в). Ток в выделенной ветви также равен нулю.

4. Последовательно с источником напряжения , включаем ещё один источник напряжения , направленный навстречу, величина ЭДС которого равна 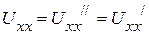(рис. 2.44 г). В результате они компенсируют друг - друга, поэтому ток в выделенной ветви 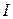равен току в исходной схеме (рис.2.44 д).

5. К полученной схеме (рис. 2.44 г) применяем метод наложения.

Алгебраическая сумма частичных токов активного двухполюсника и первого источника равна нулю (рис. 2.44 д), следовательно, ток в исходной схеме равен частичному току от добавленного источника напряжения (рис. 2.44 г). Ток в полученной схеме равен

,

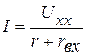где 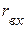– входное сопротивление пассивного двухполюсника, полученного из активного двухполюсника.

Основные этапы рассмотрим на примере расчета тока в электрической цепи, представленной на рисунке 2.45.

Рисунок 2.45 – Электрическая цепь

1. Определяем _.

1.1. Удаляем из схемы и вычерчиваем схему активного двухполюсника (рис. 2.45).

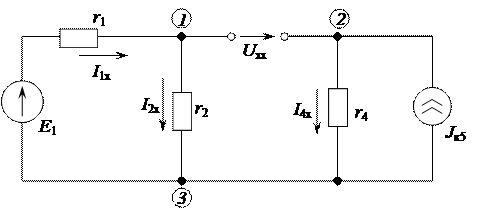
Рисунок 2.45 – Схема активного двухполюсника

1.2. Определяем токи в схеме двухполюсника:

.

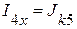1.3. Определяем . Согласно второго закона Кирхгофа имеем:

=> .

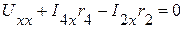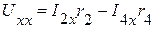2.Определяем входное сопротивление.

2.1. Из схемы активного двухполюсника удаляем источники питания и заменяем их внутренними сопротивлениями. В результате схема пассивного двухполюсника имеет вид, представленный на рисунке 2.46.

Рисунок 2.46 – Схема пассивного двухполюсника

2.2. Входное сопротивление соответственно равно:

.

3. Ток в схеме (рис. 2.45) равен:

.

Пример 2.16. Рассмотрим рекомендованный порядок расчета на конкретном примере электрической цепи, рассмотренной в примере 2.14 и представленной на рисунке 2.48, для определения тока 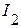. Принимаем E₁ = 50 B, Е₅ = 60 В, J_k4 = 5 А, r₁ = 10 Ом, r₂ = 8 Ом, r₃= 15 Ом, r₄ = 20 Ом.

Рисунок 2-48 - Схема электрической цепи

1. Определяем напряжение холостого хода .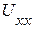

1.1. Удаляем из исходной схемы сопротивление 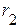и вычерчиваем схему активного двухполюсника (рис. 2.49).

Рисунок 2.49 - Схема активного двухполюсника

1.2. Определяем токи в схеме активного двухполюсника:

А, А.

1.3. Определяем U_xx по второму закону Кирхгофа:

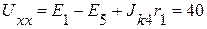, B.

2. Определяем входное сопротивление пассивного двухполюсника.

2.1. Удаляем источники питания и вычерчиваем схему пассивного двухполюсника (рис. 2.50).

Рисунок 2.50 - Схема пассивного двухполюсника

2.2. Определяем входное сопротивление: Ом.

3. Определяем ток 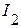: 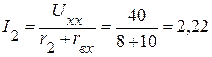А.

Величина тока 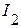, рассчитанная в примерах 2.14 и 2.16, совпадает.

Пример 2.17.Определим ток 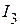методом эквивалентного генератора для электрической цепи, рассмотренной в примере 2.2.

1. Определяем напряжение холостого хода .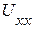

1.1. Удаляем из исходной схемы сопротивление 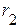и вычерчиваем схему активного двухполюсника (рис. 2.51).

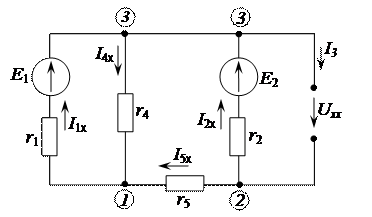
Рисунок 2.51 - Схема активного двухполюсника

1.2. Определяем токи в схеме активного двухполюсника (рис. 2.52), используя метод узловых потенциалов.

Рисунок 2.52 – Схема активного двухполюсника

1.2.1 Осуществляем предварительный анализ схемы. Количество ветвей – 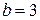, количество узлов – .

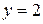Потенциал первого узла принимаем равным нулю: 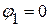. Следовательно, необходимо определить потенциал .

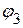1.2.2. Составляем уравнение для определения потенциала :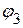

.

1.2.2.1. Подставляем числовые значения и находим потенциал .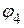

1.2.2.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:

См;

Узловые токи

А.

1.2.2.3. После подстановки цифровых значений, определяем потенциал 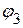: В.

1.2.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.51.

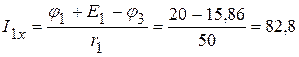мА,

мА,

мА.

1.3. Определяем 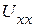по второму закону Кирхгофа (рис. 2.51):

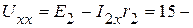
B.

2. Определяем входное сопротивление пассивного двухполюсника.

2.1. Удаляем источники питания и вычерчиваем схему пассивного двухполюсника (рис. 2.53).

Рисунок 2.53 - Схема пассивного двухполюсника

2.2. Определяем входное сопротивление:

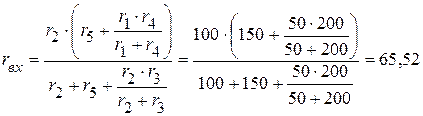Ом.

3. Определяем ток 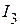: мА.

Величина тока 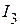, рассчитанная в примерах 2.2 и 2.17, совпадает.

Теорема компенсации

В уравнениях 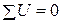, составленных по второму закону Кирхгофа, напряжение на любом сопротивлении можно всегда из левой стороны перенести в правую со знаком минус и рассматривать как эквивалентную ЭДС 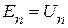, направленную противоположно току в ветви 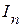. Это положение носит название принципа компенсации.

Рассмотрим применение теоремы компенсации на кокретном примере (рис. 2.54).

На рисунке 2.54 а, выделена ветвь с сопротивлением , по которой протекает ток 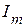. Остальная часть схемы представлена в виде активного двухполюсника. Падение напряжения на сопротивление , заменим эквивалентным источником напряжения, равным (рис. 2.54 б).

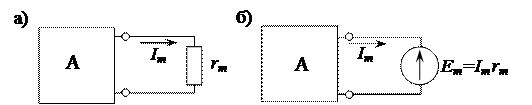
Рисунок 2.54 – Теорема компенсации

Таким образом, согласно теореме компенсации, в разветвленных электрических цепях любой резистивный элемент можно заменить эквивалентным источником напряжения, ЭДС которого равна и направлена навстречу току. Выделенный источник напряжения 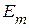работает в режиме потребления мощности 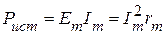(например, заряд аккумулятора). Следовательно, баланс мощностей не нарушается.

Теорему компенсации применяют при анализе и расчете разветвленных электрических цепей.

Пример 2.18.Рассмотрим применение теоремы компенсации на примере электрической цепи, изображенной на рисунке 2.55, с параметрами: E = 21 B, r₁ =100 Ом, r₂ =200 Ом, r₃ =50 Ом, r₄ =150 Ом, r₅ =75 Ом, r₆ =300 Ом.

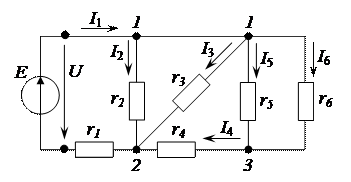
Рисунок 2.55 – Расчетная схема электрической цепи

1. Определяем параметры исходной схемы.

1.1. Определяем входное сопротивление всей цепи. Оно соответственно равно

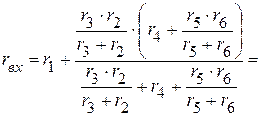
Ом.

1.2. Определяем токи в ветвях. С этой целью используем закон Ома.

1.2.1. Ток 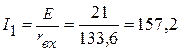мА.

1.2.2. Определяем токи , 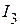и . Для их определения необходимо предварительно определить напряжение .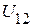

1.2.2.1. Из приведенной схемы, следует

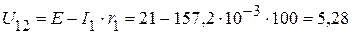В.

1.2.2.2. Тогда токи в ветвях:

мА;

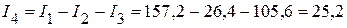мА,

мА.

1.2.3. Определяем токи и . Для их определения необходимо предварительно определить напряжение .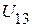

1.2.3.1. Из приведенной схемы, следует

В.

1.2.3.2. Тогда токи в ветвях:

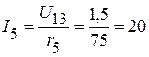мА;

мА.

2. Резистивный элемент в пятой ветви, согласно теореме компенсации, заменим источником напряжения , ЭДС которой равна В. Расчетная схема имеет вид, представленный на рисунке 2.56.

Рисунок 2.56 – Расчетная схема электрической цепи

В схеме, приведенной на рисунке 2.56, в пятой ветви подключен только источник напряжения , следовательно Ом, а проводимость данной ветви соответственно Cм. Следовательно, определяем токи во вновь полученной схеме, используя особенности метода узловых потенциалов для схем, содержащих ветви только с источником напряжения. Схема для определения токов в вевтях, приведена на рисунке 2.57.

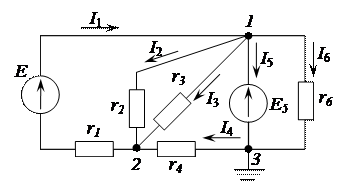
Рисунок 2.57 – Электрическая цепь постоянного тока

1. Осуществляем предварительный анализ схемы. Количество ветвей – , количество узлов – .

Принимаем потенциал 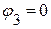, тогда В.

Следовательно, необходимо определить потенциал .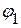

1.2.2. Составляем уравнение для определения потенциала :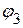

.

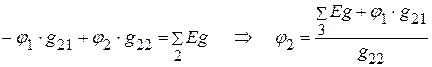1.2.2.1. Подставляем числовые значения и находим потенциал .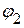

1.2.2.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:

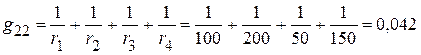См.

Узловые токи

А.

Сумма проводимостей, соединяющих различные узлы

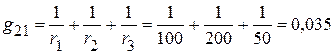См.

1.2.2.3. После подстановки цифровых значений, определяем потенциал :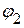

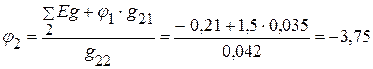В.

1.2.3. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.57.

мА,

мА,

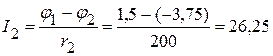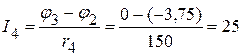мА,

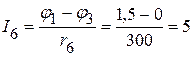мА,

мА.

Ток 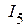определяем с использованием 1-го закона Кирхгофа для узла 3:

мА.

Величины токов 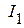, , 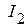, , 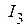, , 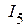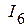рассчитанные в исходной схеме (рис. 2.55) и эквивалентной схеме (рис. 2.56), совпадает.

Свойства взаимности

Пусть в произвольной электрической цепи единственный источник напряжения с ЭДС 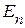действует ветви с сопротивлением в направлении от узла 1^/ к узлу 1 и в ветви с сопротивлением создает ток 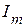, направленный от узла 2 к узлу 2^/ (рис. 2.58 а). Тогда этот же источник, будучи переключенным в ветвь с сопротивлением и действуя в направлении от узла 2 к узлу 2^/ в ветви с сопротивлением , создаст ток 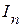, направленный от узла 1^/ к узлу 1, равный 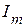(рис. 2.58 б).

Рисунок 2.58 – Пассивный четырехполюсник

Доказательство теоремы о взаимности вытекает из принципа наложения. Частичные токи равны:

— для схемы, приведенной на рисунке 2.58 а, 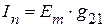— для схемы, приведенной на рисунке 2.58 б.

Так как взаимные проводимости в линейной цепи равны ( ), то соответственно равны токи в обеих схемах.

Пример 2.19.Применим принцип взаимности к электрической цепи, рассмотренной в примере 2.18 и приведенной на рисунке 2.55, состоящей из источника напряжения ЭДС которого равна В и рассчитанного тока в шестой ветви, равного 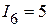мА. С этой целью, перенесем источник напряжения с ЭДС равной в шестую ветвь. С целью проверки свойства взаимности, рассчитаем ток 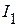во вновь полученной схеме, приведенной на рисунке 2.59.

Рисунок 2.59 – Расчетная схема электрической цепи

1. Определяем параметры исходной схемы.

1.1. Определяем входное сопротивление всей цепи. Оно соответственно равно

Ом.

1.2. Определяем токи в ветвях. С этой целью используем закон Ома.

1.2.1. Ток мА.

1.2.2. Определяем токи и . Для их определения необходимо предварительно определить напряжение .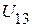

1.2.2.1. Из приведенной схемы, следует

В.

1.2.2.2. Тогда токи в ветвях:

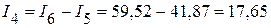мА;

мА.

1.2.3. Определяем ток 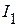. Для его определения необходимо предварительно определить напряжение .

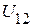1.2.3.1. Из приведенной схемы, следует

В.

1.2.3.2. Тогда ток 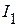равен:

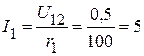мА.

Таким образом, величина тока 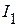, рассчитанная в эквивалентной схеме (рис. 2.59), численно равна величине тока , рассчитанной в исходной схеме (рис. 2.55), что подтверждает свойство взаимности.