Варіанти схем електричних кіл

Розрахунок усталених режимів в лінійних електричних

Колах методом контурних струмів числовими методами

Методичні вказівки

до практичних занять та лабораторних робіт

з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” для студентів електроенергетичних спеціальностей

Затверджено на засіданні

кафедри «Електричні станції»

Протокол № 1 від 28 серпня 2013 р.

Львів 2014

Розрахунок усталених режимів в лінійних електричних колах методом контурних струмів числовими методами. Методичні вказівки до практичних занять та лабораторних робіт з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” / Укл. М.С. Сегеда, Т.А. Мазур – Львів: Національний університет “Львівська політехніка”, 2014. – 26 с.

Укладачі: Сегеда М.С., професор, доктор техн. наук

Мазур Т.А., асистент

Відповідальний за випуск: Сегеда М.С., професор, доктор техн. наук

Рецензенти: Варецький Ю.О., професор, доктор техн. наук

Гоголюк П.Ф., доцент, канд. техн. наук

Мета роботи: вивчення числових методів розв’язання системи лінійних рівнянь, оволодіти навиками використання системи символьної математики МаthCad.

Основні відомості

Використання теорії графів, матрично-векторної алгебри, а також методів аналізу електричних кіл під час дослідження електромагнетних процесів у ЕЕС дає змогу створювати цифрові моделі, які працюють автоматично. Такий підхід забезпечує автоматичне формування та розв’язання рівнянь стану ЕЕС.

Найширше застосовуються під час дослідження електромагнетних процесів у ЕЕС методи аналізу електричних кіл, складених із двополюсників. Як було показано в розділі 2, використовуючи теорію графів і теорію множин, можна аналітично описати структурні елементи та фізичні величини електричного кола.

Основними фізичними величинами електричного кола є параметри заступної схеми та координати режиму. До параметрів заступної схеми елект­ричного кола належать – імпеданс (комплексний опір), складовими якого є резистанс (активний опір), реактанс (реактивний опір); адмітанс (комплекс­на провідність), яка складається з кондуктансу (активної провідності), сусцептансу (реактивної провідності). До координат режиму чи процесу (фізичні величини, які змінюються в часі) належать джерело ЕРС, джерело струму, струм, напруга, заряд, магнетний потік, напруженість електрич­ного та магнетного полів тощо. У деяких джерелах координати режиму називають ще параметрами режиму чи змінними стану.

Приклади розрахунку

для схеми, зображеної на рис. 1, обчис­лити струми та напруги віток електричного кола методом контурних струмів числовими методами: - простої ітерації; - ітерації Зайделя; - найшвидшого спуску (градієнтний метод), з точністю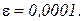

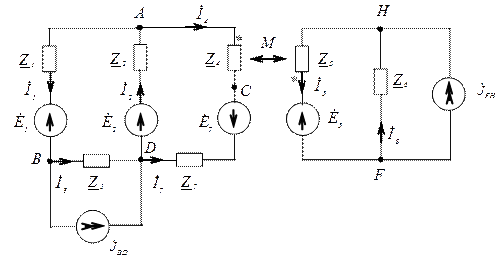
Рис. 1. Схема електричного кола

Дано: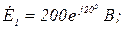

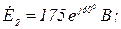
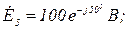
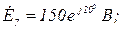
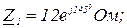
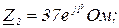
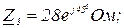
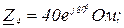
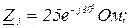
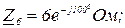
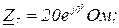
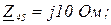
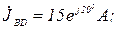
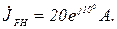
Розв’язання.

Рівняння методу контурних струмів має вигляд

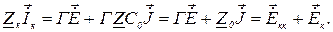
Граф схеми електричного кола (рис. 1) показано на рис. 2.

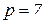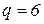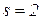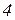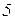Схема має віток, вузлів, електрично не зв’яза­них схем, а між опорами віток і є взаємоіндуктивний зв’язок. Граф схеми електричного кола наведено на рис. 2.

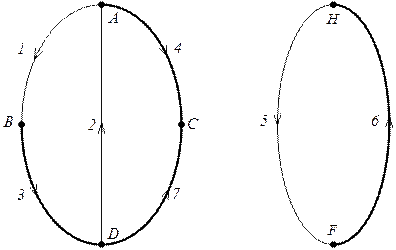
Рис. 2. Граф заступної схеми електричного кола

Серед вершин графа вузол 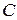є елементарним. Вузли 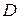і 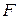приймаємо за базові.

Формуємо матриці, які описують структуру, параметри та координати електричного кола:

- перша матриця інциденцій

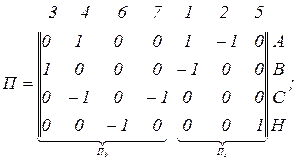
- обернена матриця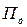

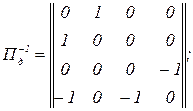
- друга матриця інциденцій

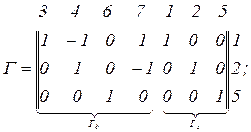
- матриця імпедансів

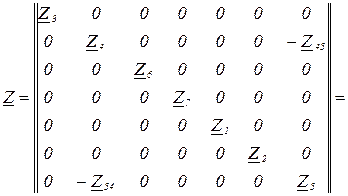
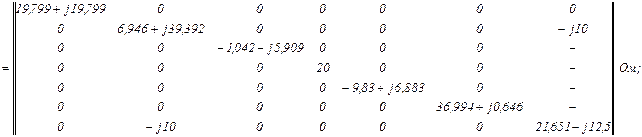- матриця коефіцієнтів розподілу розімкненої системи

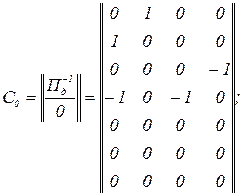
- вектор ЕРС

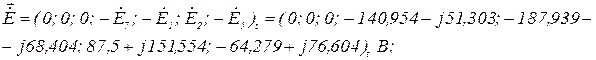- вектор джерел струму

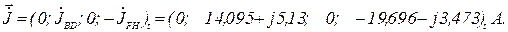
Відповідно формуються вектори струмів та напруг віток, тобто

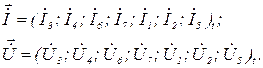
Матриця перетворення контурних струмів, обчисливши попереднь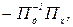о тобто

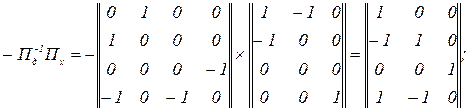
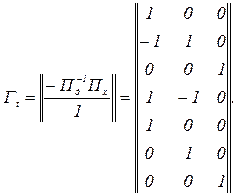
Матриця контурних імпедансів

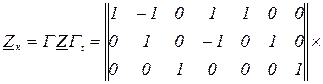
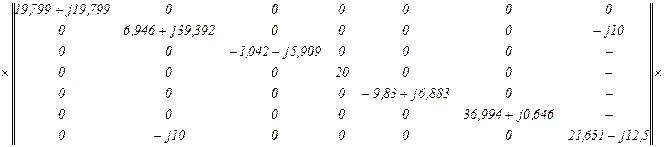
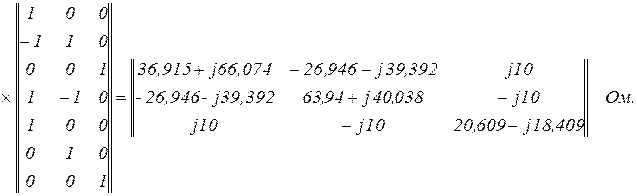
Обчислюємо обернену матрицю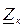

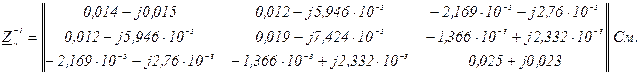Матриця перетворення ДС в еквівалентні ЕРС

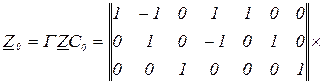
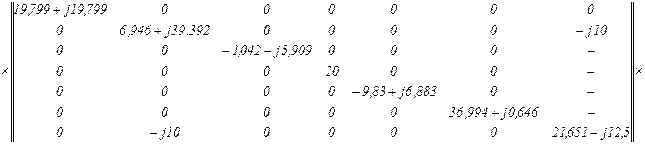
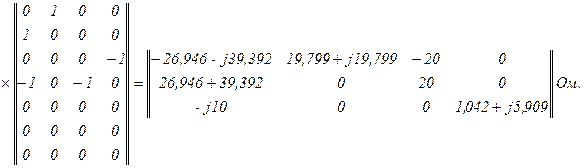
Вектор еквівалентних ЕРС, зумовлених ДС

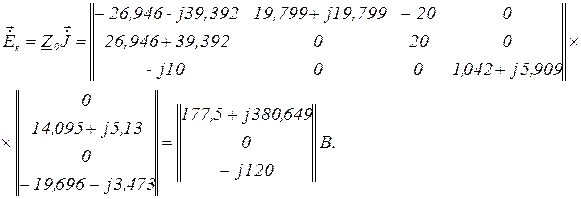
Вектор контурних ЕРС

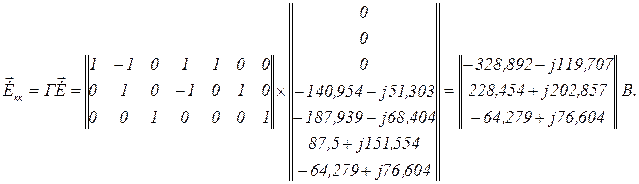
Метод простої ітерації.

Отриману систему рівнянь зводимо до явної форми множенням його на матрицю розчеплення 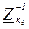(обернена діагональна матриця, елементи якої дорівнюють оберненим значенням елементів матриці 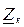) та додавши і віднявши в лівій частині системи рівнянь 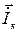, отримуємо рекурентну формулу методу простої ітерації

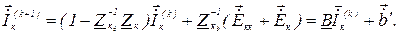
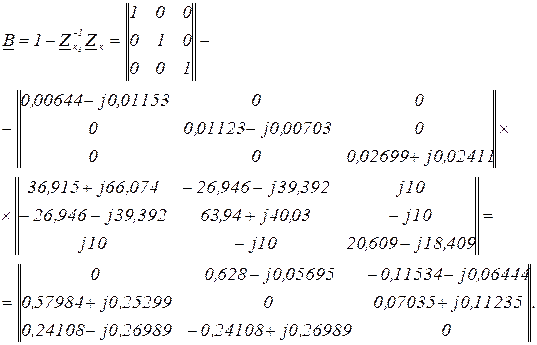
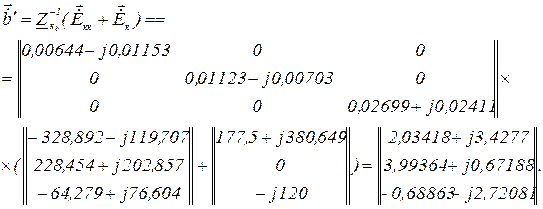
Умова збіжності ітераційного процесу визначається однієї з норм матриці, тобто

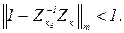
Норма матриці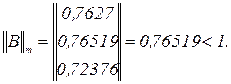

За нульове наближення контурного струму приймаємо

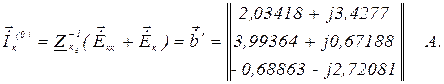
Перша ітерація.

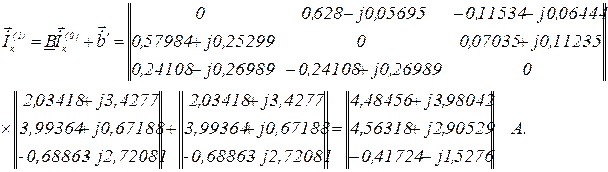
Перевірка точності

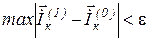, тобто

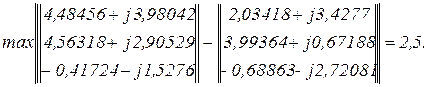
Друга ітерація.

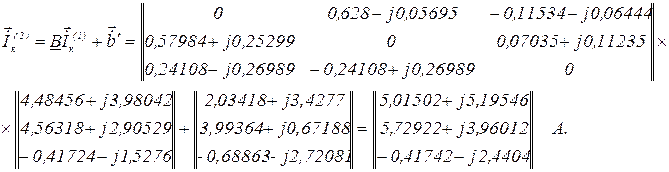Перевірка точності

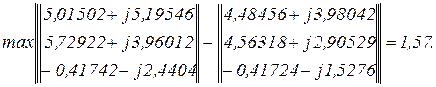
Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми 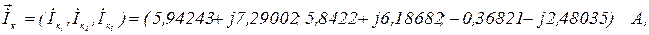кількість ітерацій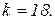

Метод ітерації Зайделя.

У методі ітерації Зайделя для обчислення «старших» невідомих 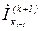використовують наближення молодших невідомих, обчислених на цьому самому кроці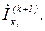

Рекурентну формулу методу ітерації Зайделя запишемо у розгорнутій формі, тобто

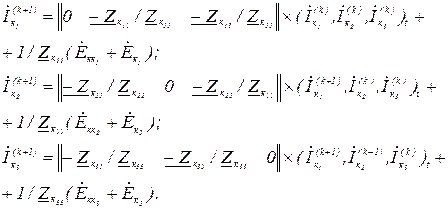
Умови збіжності ітераційного процесу оцінюються як і в методі простої ітерації.

нульове наближення вектора контурних струмів обчислюємо так

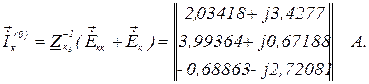
Перша ітерація.

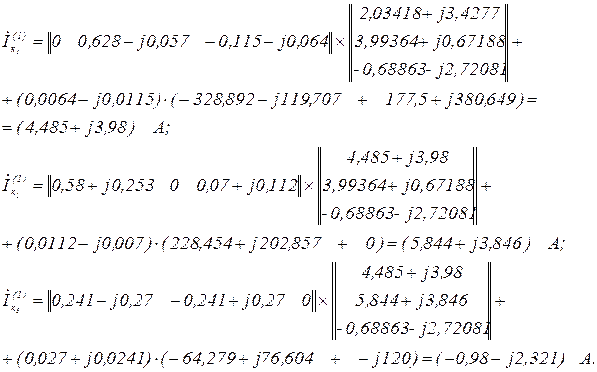
Перевірка точності

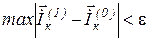, тобто

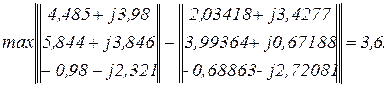
Друга ітерація.

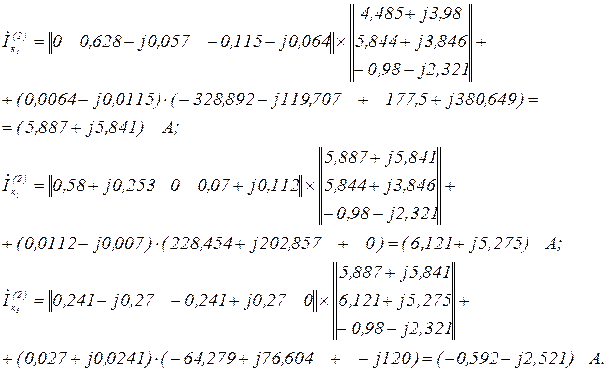
Перевірка точності

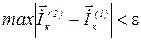, тобто

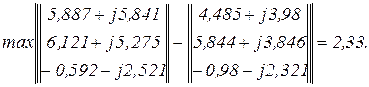
Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми 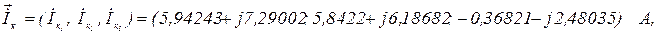кількість ітерацій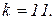

Метод найшвидшого спуску.

За нульове наближення контурних струмів приймаємо нульові наближення обчислені у методі простої ітерації.

Для лінійного комплексного векторного рівняння 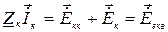з матрицею 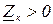задача знаходження мінімуму розв’язується перетворенням рівнянь із комплексної площини у дійсну, що призводить до подвоєння порядку рівнянь системи. Таке перетворення наведено в [1, 2], тобто увівши позначення

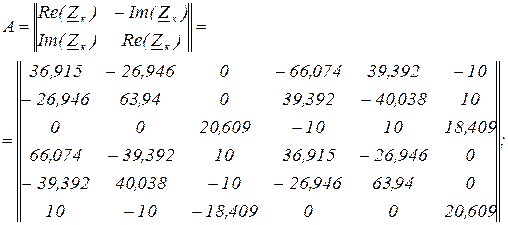
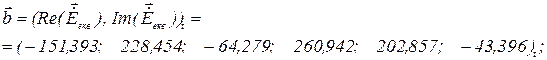
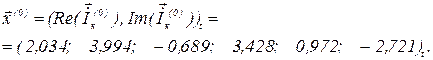
Ураховуючи, що для лінійного векторного рівняння 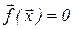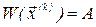та 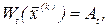обчислення 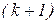-го наближення можна виконати за таким алгоритмом:

1) за знайденим на попередньому 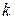-му кроці наближенням 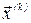знаходимо багатовимірний вектор нев’язок, тобто

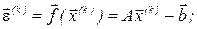
2) обчислюємо вектор

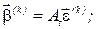
3) визначаємо вектор

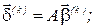
4) шукаємо параметр ітерації

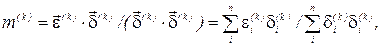
де 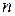– порядок системи рівнянь;

5) знаходимо наступне 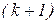-е уточнення невідомого багатовимірного вектора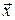

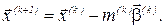
Точність розв’язання системи рівнянь методом найшвидшого спуску, як, зрештою, всіх числових методів, часто оцінюється евклідовою нормою, тобто

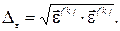
Перша ітерація.

Вектор нев’язок

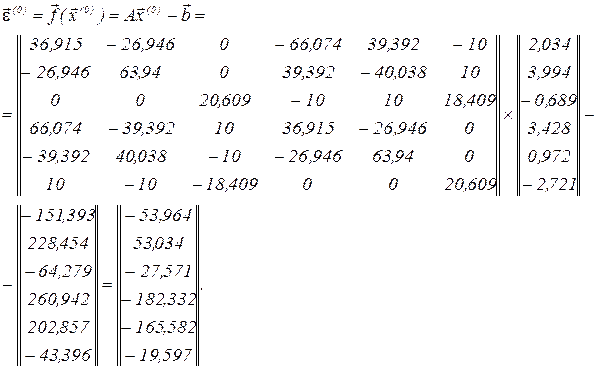
обчислюємо вектор

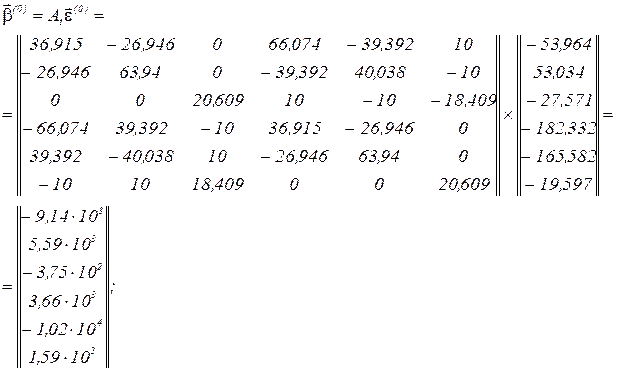
визначаємо вектор

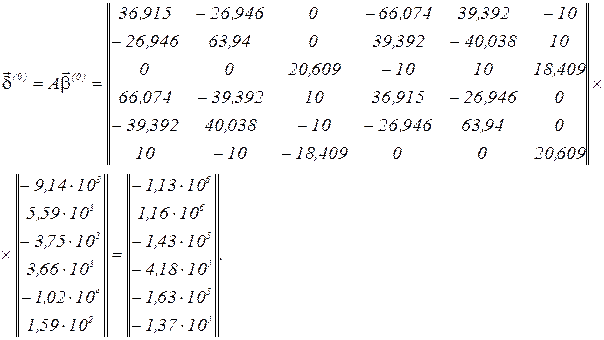
Обчислюємо параметр ітерації

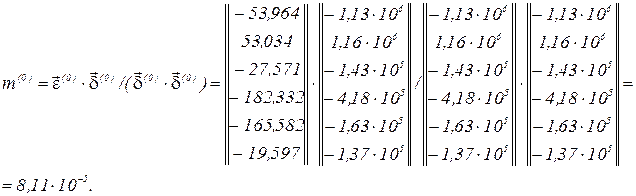
Обчислюємо перше наближення

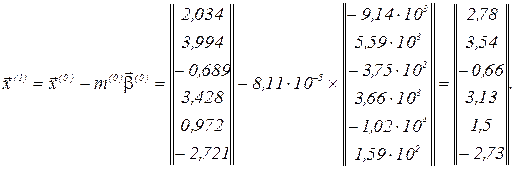
Обчислюємо евклідову норму

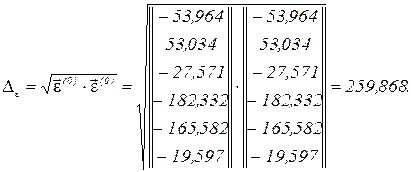
Друга ітерація.

Вектор нев’язок

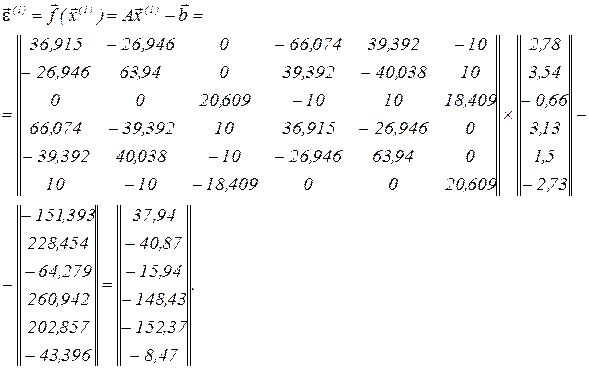
обчислюємо вектор

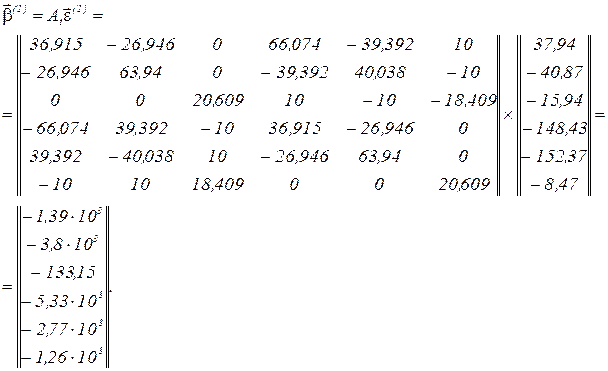
Обчислюємо вектор

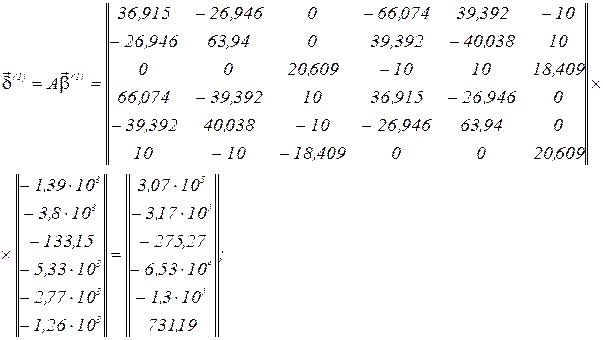
Обчислюємо параметр ітерації

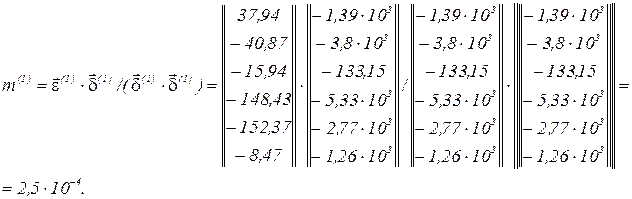
Обчислюємо друге наближення

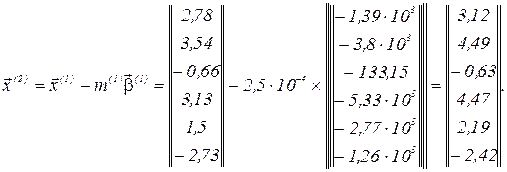
Обчислюємо евклідову норму

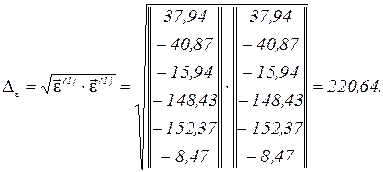
Розрахунок закінчується після досягнення заданого значення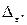

Використовуючи систему символьної математики МаthCad в ітераційному циклі обчислюємо контурні струми

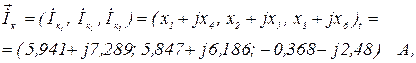
кількість ітерацій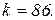

Обчислюємо струми віток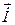

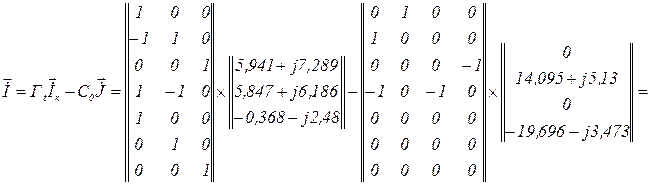
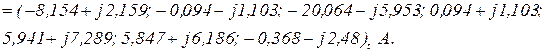
Напруга віток визначається на підставі рівняння віток

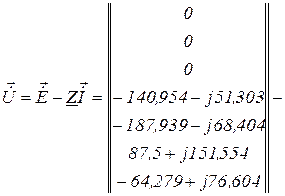
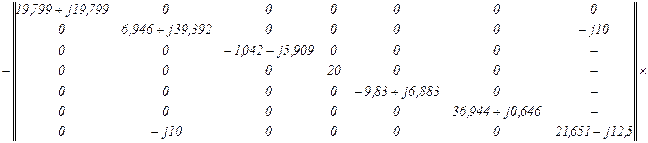
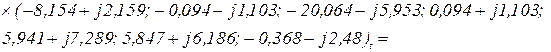
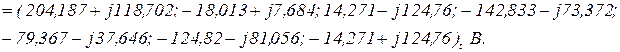
План роботи

1. Ознайомитися з теоретичними відомостями до лабораторної роботи.

2. Вибрати завдання згідно вказаного викладачем варіанту.

3. Намалювати граф електричного кола.

4. Сформувати математичну модель.

5. Використовуючи систему символьної математики МаthCad обчислити контурні струми та струми і напруги віток.

6. висновки.

Оформлення звіту

У звіті необхідно навести:

– мету та план роботи;

– короткі теоретичні відомості;

– схему електричного кола та граф схеми;

– матриці, що описують граф електричного кола, параметри та координати електричного кола;

–математичну модель у методі контурних струмів;

– результати розрахунку;

– висновки.

5. Контрольні запитання

1. Як звести систему скінченних лінійних рівнянь до явної форми?

2. Запишіть рекурентну формулу розв’язання системи скінченних лінійних рівнянь методом простої ітерації.

3. За якими умовами оцінюється збіжність розв’язання системи скінченних лінійних рівнянь методом простої ітерації?

4. Як оцінюється швидкість збіжності методу простої ітерації?

5. За яким алгоритмом розв’язується система скінченних лінійних рівнянь методом ітерації Зайделя?

6. За якими умовами оцінюється збіжність розв’язання системи скінченних лінійних рівнянь методом ітерації Зайделя?

7. У чому полягає суть методу найшвидшого спуску розв’язання системи скінченних лінійних рівнянь?

8. Запишіть рекурентну формулу методу найшвидшого спуску розв’язання системи скінченних лінійних рівнянь.

9. За яким алгоритмом обчислюють корені системи скінченних лінійних рівнянь методом найшвидшого спуску?

10. Як оцінюється точність розв’язання системи скінченних лінійних рівнянь методом найшвидшого спуску?

Список літератури

1. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / – Львів: Вид-во нац. ун-ту «Львівська політехніка», 2010. – 608 с.

2. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / 2-е вид. – Львів: Видавництво Львівської політехніки, 2013. – 608 с.

3. Перхач В.С. Математичні задачі електроенергетики – 3-е вид., перероб. і доп. – Львів: Вища шк., 1989. – 464 с.

4. Сегеда М.С. Математичне моделювання в електроенергетиці: Навч. посібник / Мін. освіти і науки України; Національний університет “Львівська політехніка” – Львів: Видавництво Національного університету “Львівська політехніка”, 2002. – 300 с.

5. Чуа Л.О., Пен-Мин Лин. Машинный анализ электрических схем (алгоритмы и вычислительные методы). – М.: "Энергия", 1980. – 640 с.

Завдання

Варіанти схем електричних кіл

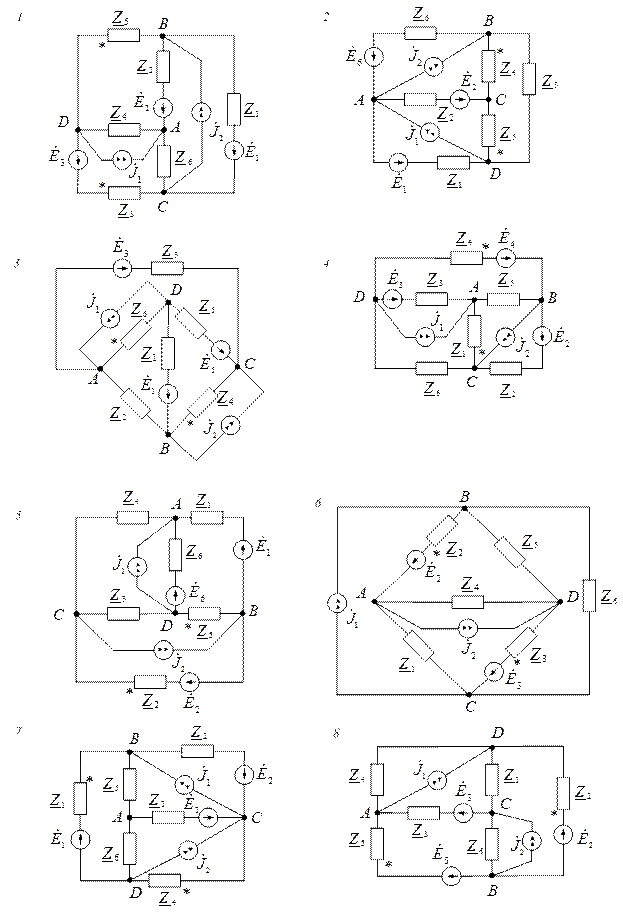
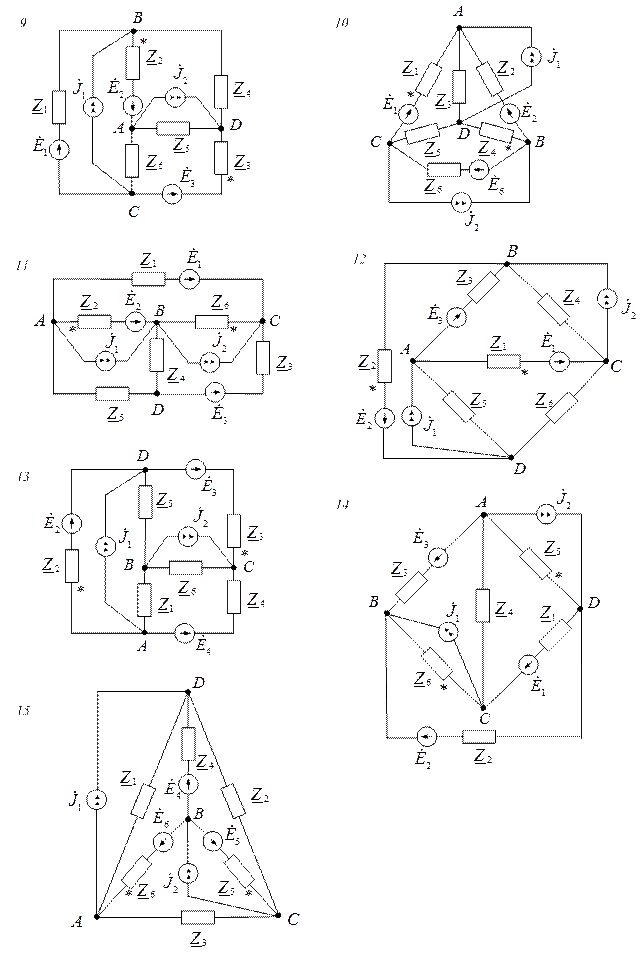
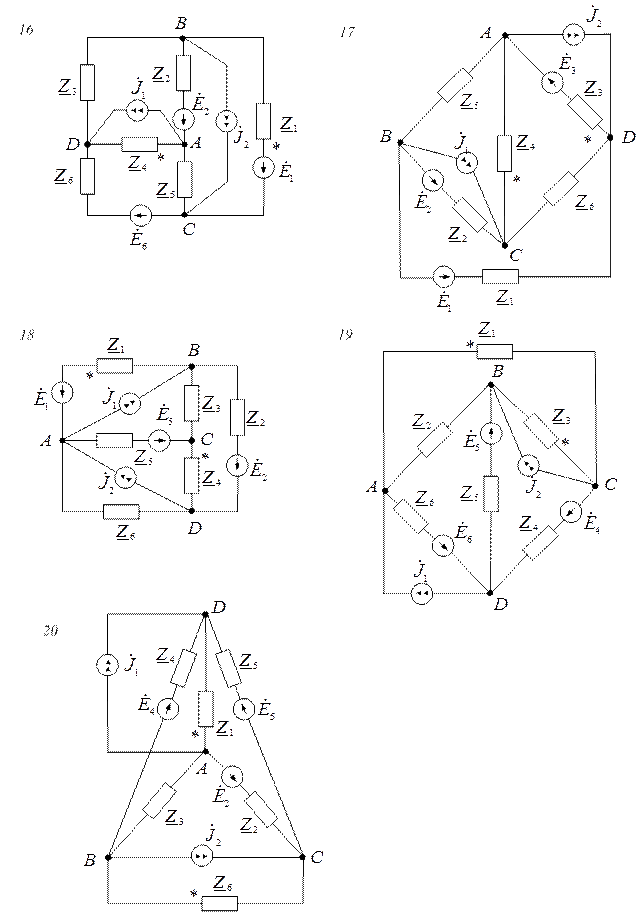
Вихідні дані до завдань

№ вар.	№ схеми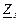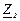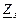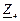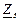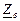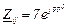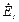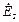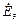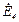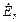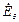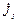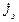
Ом	В	А
1	1											-	-	-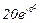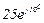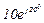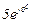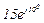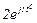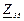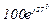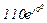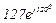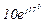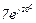
2	2										-	-	-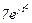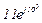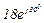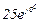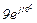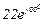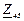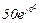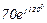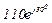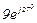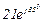
3	3									-		-		-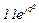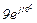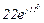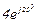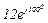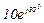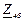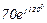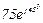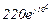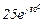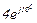
4	4								-				-	-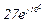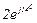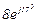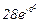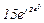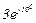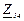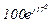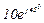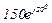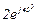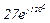
5	5										-	-	-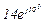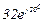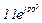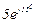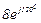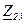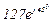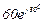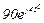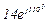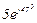
6	6								-			-	-	-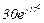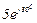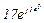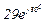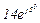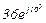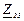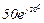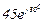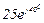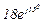
7	7											-	-	-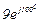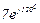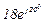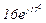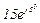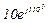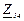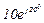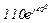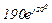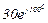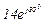
8	8								-			-		-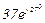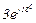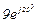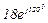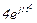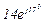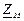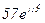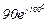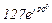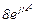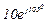
9	9											-	-	-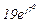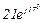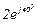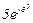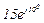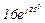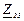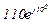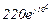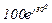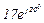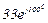
10	10										-	-	-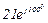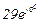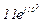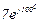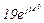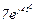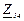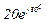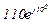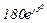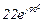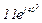
11	11											-	-	-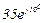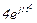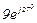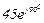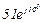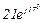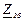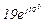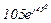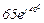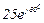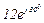
12	12											-	-	-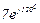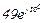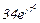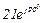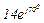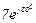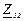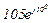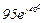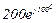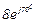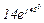
13	13								-				-	-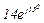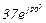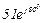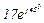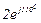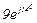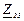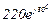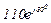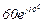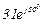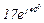
14	14											-	-	-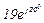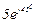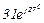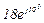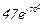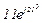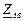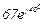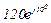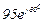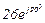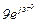
15	15								-	-	-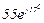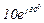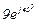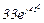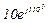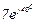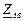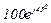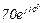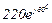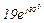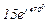
16	16										-	-	-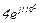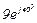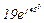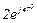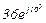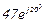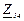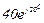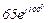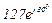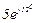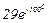
17	17											-	-	-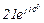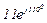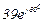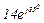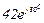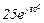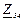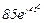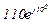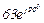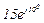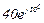
18	18										-	-		-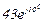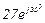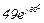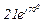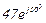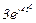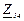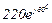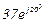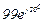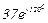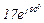
19	19								-	-	-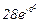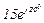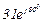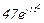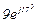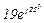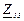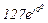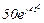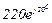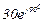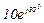
20	20								-		-			-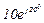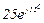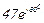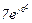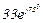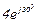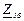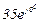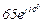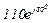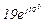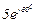

Зміст

1. Основні відомості………………………………………….

2. приклади розрахунку…………………………………………………...

3. План роботи………………………………………………………………

4. Оформлення звіту………………………………………………………..

5. Контрольні запитання……………………………………………………

Список літератури ……………………………………………………………………..

Завдання …………………………………………………………..

НАВЧАЛЬНЕ ВИДАННЯ

Розрахунок усталених режимів в лінійних електричних колах методом контурних струмів числовими методами

Методичні вказівки до практичних занять та лабораторних робіт з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” / Укл. М.С. Сегеда, Т.А. Мазур – Львів: Національний університет “Львівська політехніка”, 2014. – 26 с.

Укладачі Сегеда М.С., професор, доктор техн. наук

Мазур Т.А., асистент

Редактор

Комп’ютерне верстання