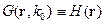Условия квазистационарности поля

1) Мы уже рассмотрели:

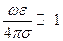
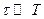
2) Характерные параметры линейного проводника 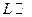характерных параметров поля .

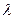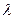- расстояние, на котором поле существенно меняется за время 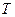(если пускаем волну, то 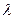- длина волны; если изменение поля гармоническое, то 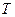- период).

3) Если длина пробега носителя тока – электрона 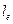, то она гораздо меньше параметра поля 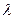, т.е. .

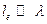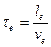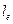4) Если носителями тока являются перемещающиеся электроны, то вводим характеристику , где - длина пробега электрона, а 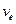- его скорость. Тогда:

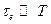
3) и 4) позволяют записывать закон Ома без учёта пространственно-временной дисперсии, в простой форме: .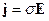

Глубина проникновения квазистационарного электромагнитного поля.

Уравнения Максвелла в случае квазистационарности:

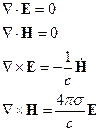
Здесь учтено, что 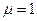и .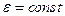

На два последних уравнения Максвелла подействуем :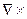

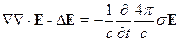
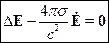- уравнение квазистационарного поля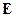

Аналогично получаем для :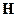

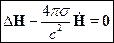
Пусть 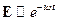; 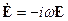, тогда:

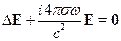
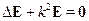
где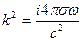

Размерность

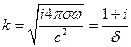
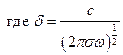- параметр глубины проникновения поля 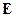. Мы получили уравнение Гельмгольца:

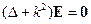
Вид решения для 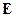зависит от формы области, где ищется решение. Если ищем в полуплоскости, то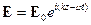

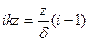- если взять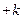

тогда получим 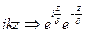. Это даёт граничное условие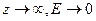

Если взять 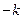, то это даст граничное условие 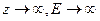, не объясняется ни физически, ни подтверждается экспериментально. Таким образом, следует брать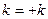

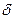-параметр: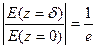

Для поля 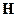аналогично:

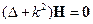
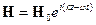- решение для полупространства.

Будем учитывать проникновение поле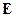й и 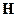только на глубину 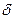, т.к. дальше их проникновение мало и его можно не учитывать, хотя оно существует.

Функция Грина уравнения Гельмгольца.

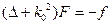-уравнение Гельмгольца

в правой части этого уравнения – источник 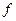, в левой – поле 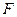источника .

,

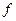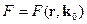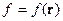
Для нахождения решения уравнения Гельмгольца вводят функцию Грина, удовлетворяющую условию:

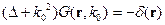
Здесь надо использовать разложение функции Грина в интеграл Фурье:

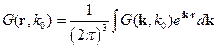
где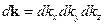

Для 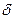-функции :

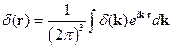
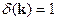
Подействуем на функцию Грина оператором :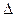

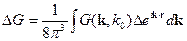
Используем то , что 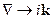, а следовательно :

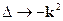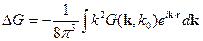
Тогда 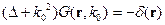перепишется в виде:

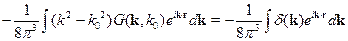
Равенство этих интегралов приводит к равенству фурье-образов:

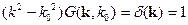
Тогда фурье-образ функции Грина:

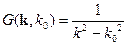
Теперь надо найти оригинал. Используем для этого теорию вычетов:

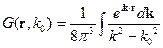
Пусть 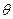- угол между 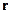и 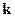. Обозначим 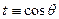. Введём сферические переменные .

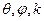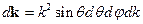
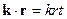, тогда 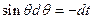.Следовательно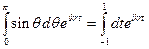

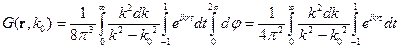
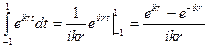
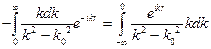
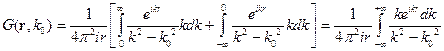
Используем теорию вычетов. У этого интеграла есть два полюса: 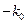и 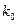. Надо использовать при расчёте полюс 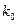, чтобы получить физически обоснованную ассимптотику.

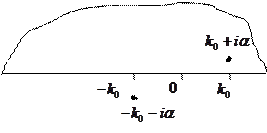Переходим в комплексную плоскость, замыкаем контур обхода сверху. Используем фиктивный переход:

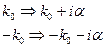
Это позволяет получить нужную асимптотику.

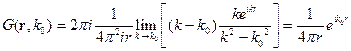
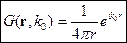- функция Грина уравнения Гельмгольца

Обозначим