Дискретный статистический ряд распределения.

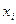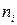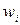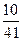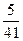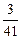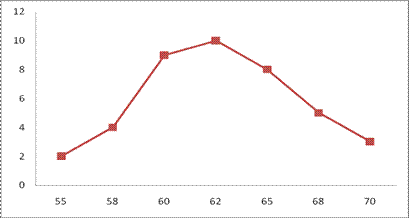
Полигон частот

Мода М₀=62. Медиана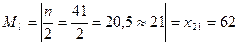

Выборочная средняя

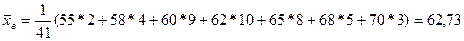– средняя частота пульса у некурящих студентов-медиков.

Выборочная дисперсия

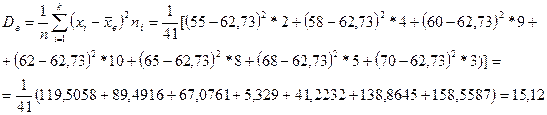
Выборочное среднее квадратическое отклонение: .

Найдем меру относительного разброса данных: коэффициент вариации

.

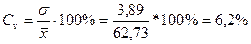Величина коэффициента вариации, равная 6,2%, свидетельствует о слабом разнообразии признака. Таким образом, изучаемую совокупность можно считать однородной.

Величину отклонения выборочного показателя от его генерального пара­метра называют стандартной ошибкой среднего (нельзя путать со средним квадратичным от­клонением изучаемой случайной переменной):

Доверительный интервал для выборочного среднего значения находится между границами 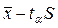и , где 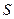- стандартная ошибка среднего, - коэффициент Стьюдента, величина, зависящая от объема выборки (или соответствующего числа степеней свободы ) и выбранного уровня доверительной вероятности, определяется по таблицам распределений Стьюдента.

Интервальный статистический ряд распределения

Определим количество интервалов по формуле Стерджеса.

Определим величину шага интервала .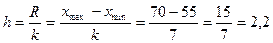

Интервалы группировки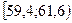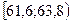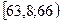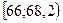
Частоты

Гистограмма частот

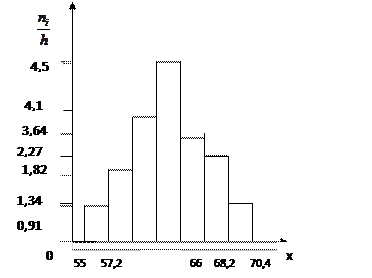
Правило 3-х сигм

Ø 68,25% всех значений лежит в интервале 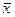±σ;

Ø 95,44% всех значений лежит в интервале 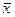±2σ;

Ø 99,73% всех значений лежит в интервале 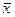±3σ.

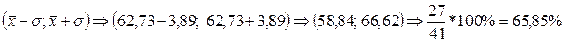, т.е. в интервале 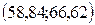расположено 27 вариант из 41, что составляет 65,85% от объема выборки.

,

.

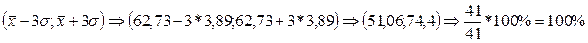Согласно этим данным можно сделать вывод, что выборка подчиняется нормальному закону распределения.

Задания

1. Изучалось среднее артериальное давление ( мм.рт.ст.) в начальной стадии шока. По случайной выборке объема 50: 112, 110, 107, 103, 108, 109, 111, 110, 103, 103, 109. 102, 113, 106, 105, 108, 104, 99, 112, 112, 103, 101, 98, 100, 97. 98. 100, 98, 107, 108, 99, 98, 92, 98, 110, 106, 105, 102, 100, 101, 100, 95, 100, 105, 100, 102, 102, 99, 97, 100. Найти дискретный , интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).

2. Изучался рост (см) мужчин возраста 25 лет для сельской местности. По случайной выборке объема 35: 175, 167. 168, 169, 168, 170,174, 173, 177, 172, 174, 167, 173, 172, 171, 171, 170, 167, 174, 177, 171, 172, 173, 169, 171, 173, 173, 168, 173. 172, 166, 164, 168, 172, 174. Найти дискретный , интервальный ряды распределения, моду, медиану, выборочную среднюю, дисперсию, среднее квадратическое отклонение, доверительный интервал. Построить полигон частот, гистограмму частот, гистограмму относительных частот. Проверить подчиняется ли выборка нормальному закону распределения (выполнение правила 3-х сигм).

Литература

Основная литература

1. Адибаев Б.М. Элементы математической статистики и основы теории верятностей. Учебное пособие, Алматы 2004г.

2. Баврин И.И. Краткий курс высшей математики. Учебник для химико-биологических и медицинских специальностей. Москва . 2003г.

3. Павлушков И.В. Основы высшей математики и математической статистики. Учебник для медицинских и фармацевтических вузов. М., 2003г.

4. Е.А.Лукьянова Медицинская статистика. Москва. Издательство Россиского университета дружбы народов.2002г.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., «Высшая школа», 2002г.

6. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа, 2001г.

7. Морозов В.Ю. Основы высшей математики и статистики. Москва. Медицина. 2001г.

8. Турецкий В.Я. Математика и информатика. Москва. ИНФРА-М. 2004г.

9. Ремизов А.Н., Максина А.Г. Сборник задач по медицинской и биологической физике. Москва. 2001г.

Дополнительная литература

1. Чистяков В.П. Курс теории вероятностей. М., «Наука», 1982г.

Статистические гипотезы в медико-биологических исследованиях.

Важное место в медицинских исследованиях занимает сравнение показателей состояния организма в норме и при потологии, до лечения и после лечения или при применении различных методов лечения. Другими словами, теория проверки статистических гипотез является основным инструментом доказательной, а не интуитивной медицины.

Одна из часто встречающихся на практике задач, связанных с применением статистических методов, состоит в решении вопроса о том, должно ли на основании данной выборки будет принято или, напротив, отвергнуто некоторое предположение (гипотеза) относительно генеральной совокупности.

Например, новое лекарство испытано на определенном числе людей. Можно ли сделать по данным результатам лечения обоснованный вывод о том, что новое лекарство более эффективно, чем применявшиеся ранее методы лечения?

ОПРЕДЕЛЕНИЕ: Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.

Задачи статистической проверки гипотез ставятся в следующем виде:

· Относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н₀.

· Из этой генеральной совокупности извлекается выборка.

· Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос

о том, следует ли отклонить гипотезу Н₀ или принять ее.