Найти общие или частные решения дифференциальных уравнений
Вариант 4
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
.
2. 
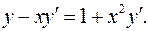
3. 
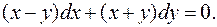
4. 
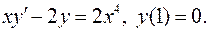
5. 
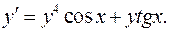
6. 
7. 
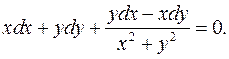
II. 8. 
Вычислить 
9. 
10. 
III.11.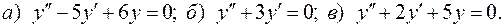 
12. 
13. 
14. 
15. Определить и записать структуру частного решения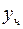 
ДУ по виду функции f(x).
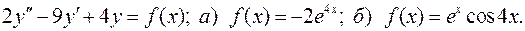
IV.16. Решить систему дифференциальных уравнений
V. 17. Записать уравнение кривой, проходящей через точку Р(1,2) и обладающей следующим свойством: площадь треугольника, образованного радиусом-вектором ОМ любой точки кривой, касательной МА в этой точке с осью Ох, равна 2.
Вариант 5
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
.
2. 
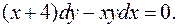
3. 
4. 
5. 
6. 
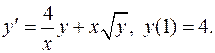
7. 
II.8. 
Вычислить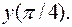 
9. 
10. 
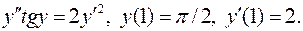
III.11. 
12 
13 
14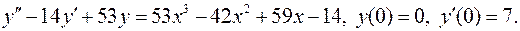 
15 Определить и записать структуру частного решения 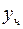ЛНДУ по виду функции f(x).
IV. 16. Решить систему дифференциальных уравнений
V. 17. В комнате, где температура 20°, некоторое тело остыло за 20 мин от 100 до 60°. Считая, что скорость остывания пропорциональна разности температур тела и воздуха в комнате и последняя повышается незначительно, найти закон остывания тела. Через сколько минут оно остынет до 30°?
Вариант 6
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 
4. 
5. 
6. 
7. 
II. 8. 
Вычислить 
. 
9. 
10. 
III.11. 
12. 
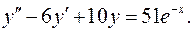
13. 
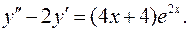
14. 
15. Определить и записать структуру частного решения 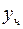ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
V.17. Найти уравнение кривой, проходящей через точку 
, у которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.
Вариант 7
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 
4. 
5. 
6. 
7. 
II. 8.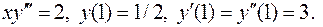 
Вычислить
9. 
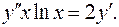
10. 
III.11. 
12. 
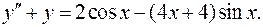
13. 
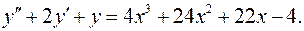
14. 
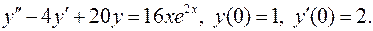
15.Определить и записать структуру частного решения 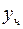ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
V. 17. Автомобиль движется по горизонтальному участку пути со скоростью v = 90 км/час. В некоторый момент времени он начинает тормозить. Сила торможения равна m = 0,3 от веса автомобиля. В течение какого промежутка времени он будет двигаться от начала торможения до полной остановки, и какой путь пройдёт за это время?
Вариант 8
Найти общие или частные решения дифференциальных уравнений.
I. 1.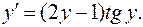 
2. 
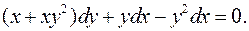
3. 
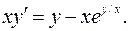
4. 
5. 
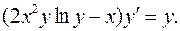
6. 
7. 
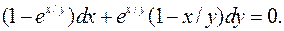
II. 8.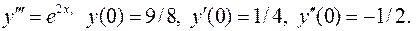 
Вычислить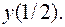 
9. 
10. 
III.11. 
12. 
13. 
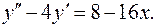
14. 
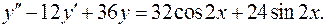
15.Определить и записать структуру частного решения 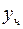ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
V. 17. Найти уравнение кривой, проходящей через точку 
, для которой отрезок, отсекаемый на оси ординат нормалью в любой точке кривой, равен расстоянию этой точки от начала координат.
Вариант 9
Найти общие или частные решения дифференциальных уравнений.
I. 1.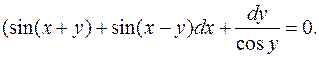 
2. 
3. 
4. 
5. 
6. 
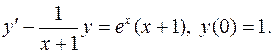
7. 
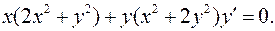
II. 8.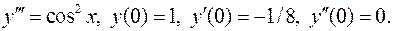 
Вычислить 
9. 
10. 
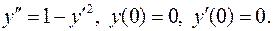
III.11. 
12. 
13. 
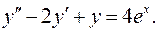
14. 
15. Определить и записать структуру частного решения 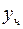ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
V. 17. Плоский контур площадью S с сопротивлением R и самоиндукцией L вращается с угловой скоростью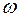 
в постоянном магнитном поле 
вокруг оси, лежащей в плоскости контура и перпендикулярно . Найти силу тока в петле, обусловленную индукцией магнитного поля.
Вариант 10
Найти общие или частные решения дифференциальных уравнений.
I. 1.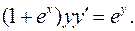 
2. 
3. 
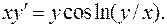
4. 
5. 
6. 
7. 
II. 8.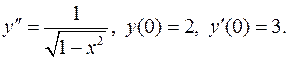 
Вычислить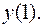 
9. 
10. 
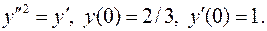
III.11. 
12 . 
13 .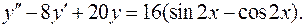 
14 . 
15 .Определить и записать структуру частного решения 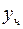ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
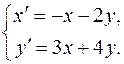
V. 17. Записать уравнение кривой, проходящей через точку А(0,4), если известно, что длина отрезка, отсекаемого на оси ординат нормалью, проведённой в любой точке кривой, равна расстоянию от точки до начала координат.
Вариант 11
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
tg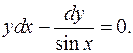 
2. 
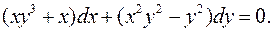
3. 
4. 
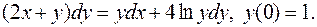
5. 
6. 
7. 
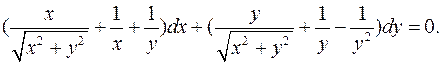
II.8. 
Вычислить 
9. 
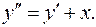
10. 
III.11.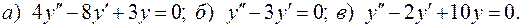 
12. 
13. 
14. 
15.Определить и записать структуру частного решения 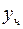ЛНДУ по виду функции f(x).
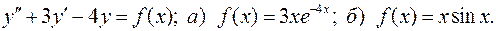
IV.16.Решить систему дифференциальных уравнений
V. 17.Шарик массой 
движется под действием упругой силы 
и силы трения 
, где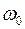 
- собственная частота колебаний шарика, 
; 
- коэффициент трения. В момент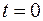 
он отстоит от точки равновесия на расстоянии 5 см и его начальная скорость равна нулю. Найти зависимость координаты шарика от времени. Через сколько времени его амплитуда уменьшится в 
раз?
Вариант 12
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
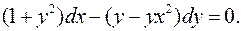
3. 
4. 
5. 
6. 
7. 
tg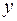 
II. 8. 
Вычислить 
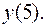
9. 
10. 
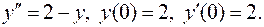
III.11. 
12. 
13. 
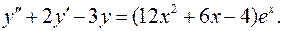
14. 
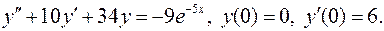
15. Определить и записать структуру частного решения 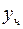ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
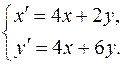
V. 17. Записать уравнение кривой, проходящей через точку А(4,1) и обладающей следующим свойством: отрезок, который касательная в любой точке кривой отсекает на оси Оу, равен квадрату абсциссы точки касания.
Вариант 13
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 
4. 
5. 
6. 
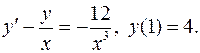
7. 
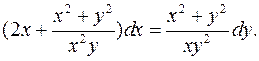
II. 8.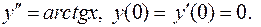 
Вычислить
9. 
10. 
III.11.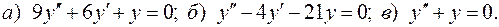 
12. 
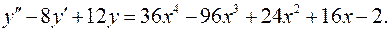
13. 
14. 
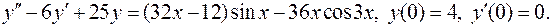
15. Определить и записать структуру частного решения 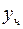ЛНДУ по виду функции f(x).
IV.16. Решить систему дифференциальных уравнений
V. 17. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости вращения. Найти зависимость этой угловой скорости от времени, если известно, что диск, начавший вращаться со скоростью 100 об/мин, по истечении 1 минуты вращается со скоростью 60 об/мин.
Вариант 14