Іі, системи диференціальних рівняннь

Рівняння, які зв’язують змінну х, невідомі функції 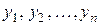та перші похідні цих функцій, утворюють канонічну нормальну систему диференціальних рівнянь першого порядку, якщо її можна зобразити у вигляді

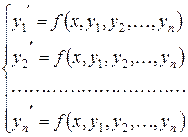(1)

Розв’язком системи (1) називають сукупність функцій 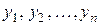, що перетворюють кожне рівняння на тотожність.

Для систем можна сформулювати задачу Коші: знайти розв’язок рівняння (1) 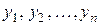, що задовольняє початковим умовам при х=х₀ .

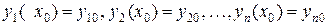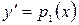Диференціальне рівняння -го порядку заміною (тоді 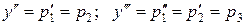і так далі) можна звести до нормальної системи диференціальних рівнянь першого порядку.

Іноді нормальну систему диференціальних рівнянь можна звести до одного рівняння порядку з однією невідомою функцією. Це може бути досягнуто диференціюванням одного з рівнянь і виключенням усіх невідомих, окрім одного (метод виключення).

Якщо праві частини нормальної системи диференціальних рівнянь є лінійними функціями відносно 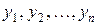, то систему називають лінійною.

Розглянемо лінійну однорідну систему диференціальних рівнянь з постійним коефіцієнтами

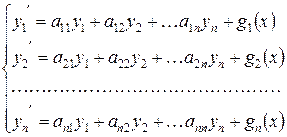(2)

Цю систему можна записати в матричному вигляді

,

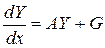де

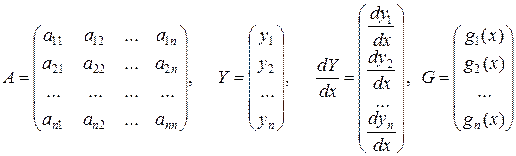(3)

Якщо всі функції 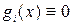, то система (2) називається однорідною.

Загальний розв’язок лінійної однорідної системи диференціальних рівнянь -го порядку визначається як лінійна комбінація його лінійно незалежних частинних розв’язків, тобто

,

де .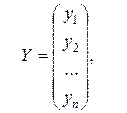

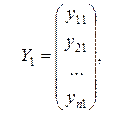
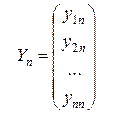Систему з лінійно незалежних розв’язків однорідної системи диференційних рівнянь називають фундаментальною системою розв’язків. Її записують квадратною матрицею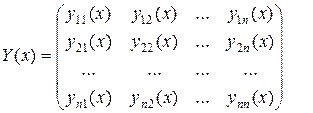

Шукаємо розв’язок однорідної системи у вигляді

, , ...,

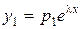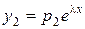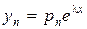(4)

Підставивши (4) в систему (2), одержимо систему лінійних алгебраїчних

рівнянь

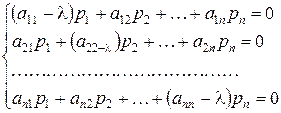(5)

Ця система має ненульовий розв’язок, якщо її визначник дорівнює нулю.

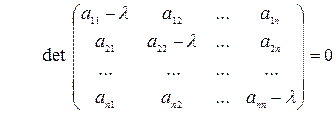(6)

Рівняння (6) – це алгебраїчне рівняння степені n , яке називається характеристичним рівнянням системи (2). Воно має n коренів 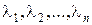. Для кожного 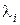з системи (5) знайдемо 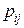, тоді загальний розв’язок лінійної однорідної системи диференційних рівнянь -го порядку можна записати так:

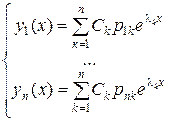(7)

Загальний розв’язок неоднорідної системи диференціальних рівнянь -го порядку (2) може бути представлений у вигляді суми загального розв’язку відповідної однорідної системи диференціальних рівнянь -го порядку і деякого частинного розв’язку неоднорідної системи.

Приклад.

1. Розв’язати систему .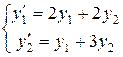

Її характеристичне рівняння (3.6) має вигляд 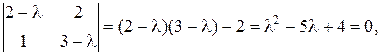його корені дорівнюють . Для кореня 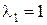складемо систему (5)

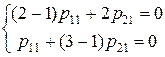, тобто .

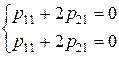Якщ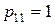о , то 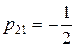. Аналогічно знаходимо 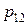і 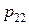для кореня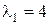

, .

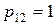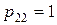Тепер можемо записати розв’язок системи відповідно до (7)

.

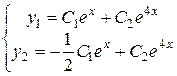2. Розв’язати систему .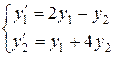

Її характеристичне рівняння (3.6) має вигляд 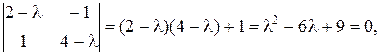рівняння має один корінь, який дорівнює .

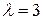Тоді розв’язок системи шукаємо у вигляді 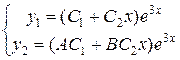, де А і В – невідомі коефіцієнти. Підставляємо цей розв’язок у систему, прирівняємо коефіцієнти при однакових степенях 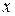і знайдемо невідомі сталі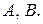

,

.

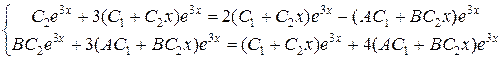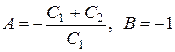Підставляємо ці значення А і В у розв’язок системи отримаємо .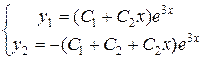

3. Розв’язати неоднорідну систему .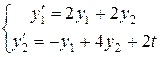

Зведемо систему до одного рівняння другого порядку. З першого рівняння виразимо 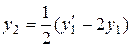і підставимо у друге 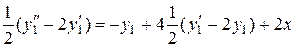. Після спрощення отримаємо лінійне неоднорідне диференціальне рівняння другого порядку 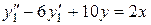. Так як 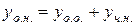, то розв’яжемо спочатку відповідне рівняння

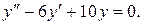Характеристичне рівняння має вид 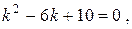його корені 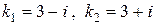. Отже,

.

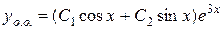Так як серед коренів характеристичного рівняння немає кореня 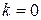, а права частина заданого рівняння представляє собою багаточлен першої степені, то 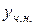шукаємо у вигляді

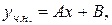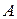де і 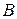- невідомі коефіцієнти.

Диференціюючи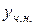

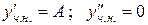і підставляючи в початкове рівняння, маємо:

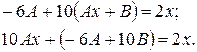
Прирівняємо коефіцієнти при однакових степенях 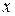в правій і лівій частині останнього рівняння:

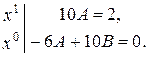
З першого рівняння знаходимо 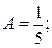із другого 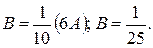Тоді 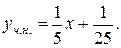Отже маємо:

.

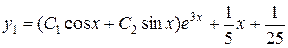Підставляючи у вираз для 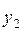отримаємо

.
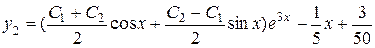