Геометрическое решение игр .
Игры с двумя стратегиями можно решить геометрически. Для этого начинаем решать игру со стороны игрока, у которого две стратегии.
Пусть этот игрок А.

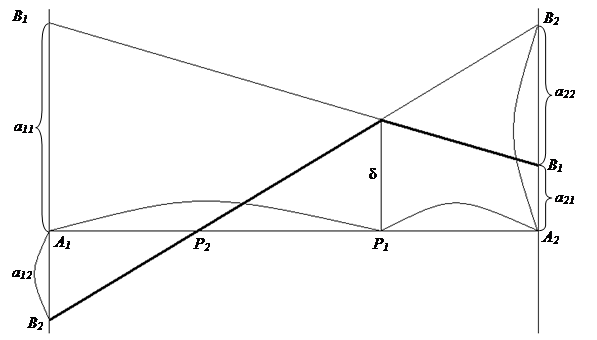
Решается по принципу минимакса для игрока А.
Решение необязательно находится на пересечении линий.
Рассмотрим задачу со стороны игрока В.
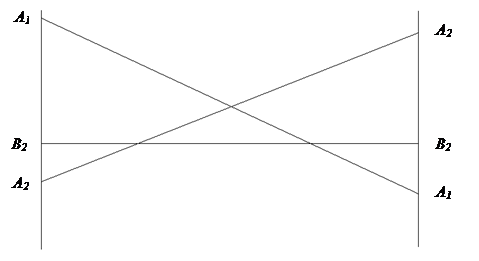
Если у одного игрока 2 стороны, а у другого много, то игру также можно решить геометрически.
В результате упрощения, игра имеет вид:
| B1 | 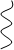 B2 B2 | 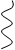 B3 B3 | B4 | |
| A1 | -1 | -3 | ||
| A2 | -1 | -5 |
Решим игру относительно игрока А:
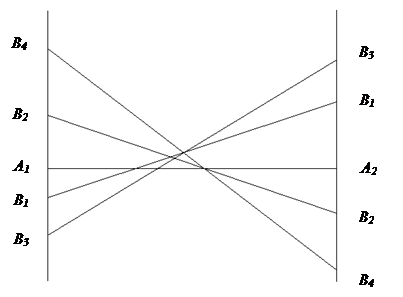 |
Для решения необходимо решить совместное уравнение В4, В1.
Тангенс угла наклона 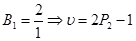
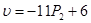
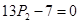
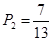
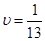
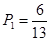
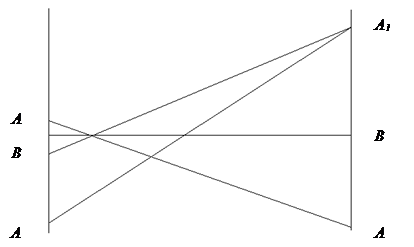 |
A1: 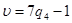
A2: 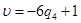
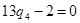
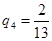
Решение игр m ´ n.
Пусть у игрока 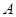 ,
, 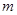 стратегий, а у
стратегий, а у 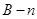 . В общем случае игра имеет решение в области смешанных стратегий. Таким образом, чтобы решить игру надо найти
. В общем случае игра имеет решение в области смешанных стратегий. Таким образом, чтобы решить игру надо найти 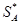 и
и 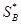 . Пусть игрок
. Пусть игрок 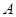 применяет свою оптимальную смешанную стратегию, а игрок
применяет свою оптимальную смешанную стратегию, а игрок 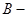 чистую. При этом поучится выигрыш:
чистую. При этом поучится выигрыш:
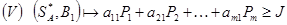
По определению решения игры, отклонение игрока 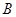 от своей оптимальной стратегии невыгодно для него. Если бы все стратегии были активными, то можно было бы поставить “ = ” в выражение
от своей оптимальной стратегии невыгодно для него. Если бы все стратегии были активными, то можно было бы поставить “ = ” в выражение 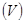 .
.
В дальнейшем будем считать, что величина цены игры 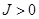 . Этого можно добиться, если первоначальную платёжную матрицу
. Этого можно добиться, если первоначальную платёжную матрицу 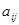 сместить вверх, т. е. прибавить величину
сместить вверх, т. е. прибавить величину 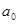 к каждому элементу матрицы. При этом решение игры не меняется.
к каждому элементу матрицы. При этом решение игры не меняется.
Разделим левую и правую часть неравенств на величину 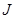 , и обозначим величины
, и обозначим величины 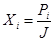 . Тогда получим систему ограничений в следующем виде:
. Тогда получим систему ограничений в следующем виде:
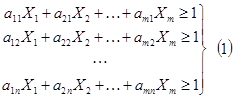
Так как 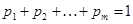 то:
то:
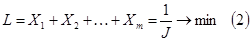
Так как необходимо выбрать такие вероятности 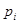 , что бы цена игры была максимальной, то можно считать, что
, что бы цена игры была максимальной, то можно считать, что 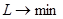 . Получили следующую задачу линейного программирования: найти такие неотрицательные величины
. Получили следующую задачу линейного программирования: найти такие неотрицательные величины 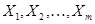 которые бы удовлетворяли системе уравнений
которые бы удовлетворяли системе уравнений 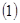 и при этом минимизировали линейную систему
и при этом минимизировали линейную систему 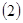 . Аналогично рассмотрим игру со стороны игрока
. Аналогично рассмотрим игру со стороны игрока 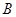 .
.
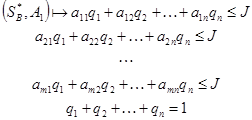
Аналогично делим на 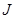 и обозначим
и обозначим 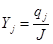 . Получим задачу:
. Получим задачу:
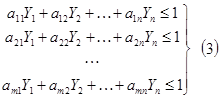
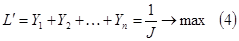
Так как игрок 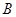 стремится уменьшить выигрыш, то решение игры
стремится уменьшить выигрыш, то решение игры 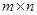 может быть сведено к решению пары задач линейного программирования.
может быть сведено к решению пары задач линейного программирования.
Рассмотрим вопрос существования решения задач 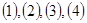 . Доказательство существования этого решения будет доказательством основной теоремы теории игр.
. Доказательство существования этого решения будет доказательством основной теоремы теории игр.
Доказательство: из теории линейного программирования известно, что задача линейного программирования не имеет решения в двух случаях:
1) Нет допустимого решения, т. е. система ограничений несовместна.
2) Целевая функция не ограничена.
Покажем, что любая пара задач линейного программирования имеет решение: возьмём 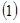 и
и 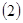 . Рассмотрим самый маленький выигрыш матрицы
. Рассмотрим самый маленький выигрыш матрицы 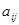 :
: 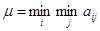 . Тогда в качестве решения можно взять следующее:
. Тогда в качестве решения можно взять следующее: 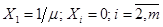 . Подставим это решение во все строки линейных неравенств
. Подставим это решение во все строки линейных неравенств 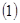 . Так как
. Так как 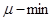 , то, например,
, то, например, 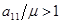 всегда, а остальные равны нулю, то у нас есть решение всегда. Так как вероятности и цена игры больше нуля, поэтому
всегда, а остальные равны нулю, то у нас есть решение всегда. Так как вероятности и цена игры больше нуля, поэтому 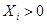 . Так как
. Так как 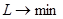 , то минимальная величина ограничена по крайней мере нулём, таким образом мы доказали, что решение
, то минимальная величина ограничена по крайней мере нулём, таким образом мы доказали, что решение 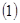 и
и 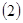 всегда существуют. А если существует
всегда существуют. А если существует 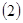 , то существует
, то существует 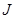 , и значит существует
, и значит существует 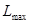 во второй задаче. Мы доказали основную теорему теории игр: любая матричная игра имеет решение в области смешанных стратегий.
во второй задаче. Мы доказали основную теорему теории игр: любая матричная игра имеет решение в области смешанных стратегий.
