Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

Рассмотрим уравнение

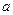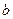где и константы, а функция 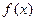в правой части уравнения имеет один из следующих трех видов

, , ,

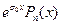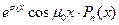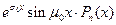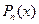- произвольный многочлен степени 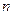. Решение такого уравнения может быть получено следующим образом. Квадратное уравнение

назовем характеристическим уравнением для нашего уравнения. Пусть , – корни этого квадратного уравнения. Общее решение однородного уравнения

имеет вид

,

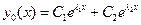если , - два различных вещественных числа; имеет вид

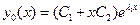
если и, наконец, решение имеет вид

если 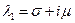, - комплексно-сопряженные корни характеристического уравнения.

Общее решение неоднородного уравнения может быть получено как сумма общего решения однородного уравнения и произвольного частного решения неоднородного уравнения . Это частное решение можно найти методом неопределенных коэффициентов по следующему правилу.

Сопоставим функции 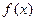в правой части исходного уравнения число 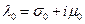. Если 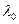не является корнем характеристического уравнения, то частное решение ищем в том же виде, в каком записана правая часть, то есть

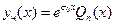
если 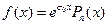, и в виде

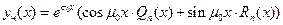
ес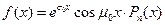ли или 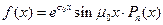. Здесь 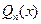, 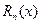многочлены степени 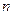, коэффициенты которых можно определить, подставив в исходное уравнение и приравняв коэффициенты при одинаковых функциях. Если 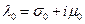является корнем характеристического уравнения (эта ситуация называется резонансом), то степень многочленов 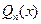, 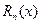увеличивается на 1.

Задача 4.2.а. Найти решение задачи Коши для дифференциального уравнения.

Решение. Сначала найдем общее решение однородного уравнения. Выпишем характеристическое уравнение

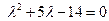Û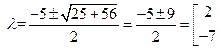

Следовательно, общее решение линейного однородного уравнения имеет вид

.

Поскольку корни характеристического уравнения не совпадают с соответствующим показателем правой части , частное решение неоднородного уравнения будем искать в виде

.

Получаем:

,

.

Подставляя , , 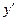в исходное уравнение, получаем:

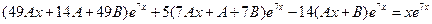Сокращая на и приводя подобные, получим

,

,

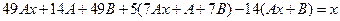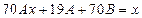откуда

Û

Общее решение неоднородного уравнения имеет, следовательно, вид

.

Теперь найдем решение задачи Коши. Имеем:

,

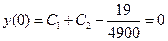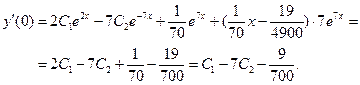
Поскольку 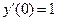, второе уравнение имеет вид 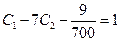. Решаем систему линейных уравнений на неизвестные 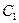и :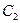

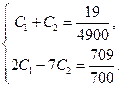
Умножая первое уравнение системы на 2 и вычитая из него второе уравнение, получим:

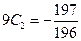Û .

Далее,

.

Ответ: .

Задача 4.2.б.Найти решение задачи Коши для дифференциального уравнения.

Решение. Характеристическое уравнение имеет вид:

,

откуда

,

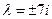где - мнимая единица. Следовательно, , , 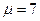и общее решение однородного уравнения есть

.

Правая часть исходного неоднородного уравнения имеет то же собственное число, что и характеристическое уравнение, следовательно, мы имеем дело с резонансом. Поэтому частное решение неоднородного уравнения следует искать в виде

.

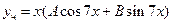Подставляя в исходное уравнение, с учетом того, что

,

получим:

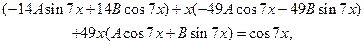
откуда

и, следовательно,

, .

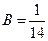Таким образом, частным решением неоднородного уравнения является функция

.

Общее решение неоднородного уравнения может быть записано в виде

.

Найдем константы 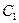и 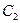, при которых выполнены краевые условия

, .

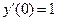Так как

,

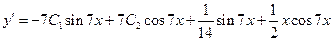получаем систему линейных уравнений на 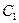и :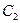

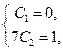
откуда .