Задача виявлення та виправлення помилок в текстах
· частота помилок від 0.05% до 38%.
· задача виявлення та виправлен я помилок вирішується в текстових процесорах, пошукових системах, системах розпізнавання текстів та рукописного тексту
· основний підхід використання імовірнісних моделей
52. Основні задачі виявлення і виправлення помилок.
· виявлення помилок, що приводять до утворення невідомих слів (graffe - giraffe, кнь-кінь)
· виправлення помилок в окремих словах
· виявлення і виправлення помилок з врахуванням контексту (there-three, ахматова-ахметова, dessert-desert, piece-peace, ріка-рука, кутати-кусати)
53. Виправлення помилок на основі порівняння стрічок.
· встановлення яке з двох слів є ближче за правописом до третього – окремий випадок порівняння стрічок (string distance)
· порівняти стрічки - встановити міру відмінності між двома послідовностями символів
· алгоритм minimum edit distance
відстань Левенштейна
54. Поняття відстань Левенштейна.
Ві́дстань Левенште́йна у комп'ютерній лінгвістиці міра відмінності двох послідовностей символів (рядків). Обчислюється як мінімальна кількість операцій вставки, видалення і заміни, необхідних для перетворення одної послідовності в іншу.Метод розроблений у 1965 році радянським математиком Володимиром Йосиповичем Левенштейном і названий його іменем.
Приклад:
Щоб перетворити слово небо на слово треба необхідно зробити дві заміни та одну вставку, відповідно дистанція Левенштейна становить 3:
1. небо -> неба (замінюємо о на а)
2. неба -> реба (замінюємо н на р)
3. реба -> треба (вставляємо т)
На практиці дистанція Левенштейна використовується для визначення подібності послідовностей символів, наприклад для корекції орфографії або для пошуку дублікатів.
55.Загальна характеристика алгоритму мінімальної відстані редагування.
· Обчислюється як мінімальна кількість операцій вставки, видалення і заміни, необхідних для перетворення одної послідовності в іншу.
· перетворення з вирівнюванням двох стрічок
d - видалення
і – вставка
s - заміна
56.Задача пошуку мінімальної відстані редагування, як пошукова задача.
· щоб отримати стрічку довжиною к потрібно зробити к операцій вставки
· щоб отримати стрічку довжиною 0 потрібно зробити к операцій видалення
· крок по горизонталі [j](по рядку) - вставка
· крок по вертикалі [i](по стовпчику) – видалення
· крок по обом індексам [i,j] – заміна, або відсутність змін коли символи співпадають
57.Правила заповнення матриці відстаней.
· заповнення першого стовпчика матриці
· і=1, j=1,2,3,4,5,6,7,8,9
Е-># видалення 1
Е->I заміна 2
Е- >IN заміна+вставка 3
Е->INT заміна+вставка+вставка 4
E-> INTE вставка+вставка+вставка 3
Е->INTEN вставка+вставка+вставка+вставка 4
58.Визначення елементів матриці відстаней
· визначаються на основі рекурсивного рівняння
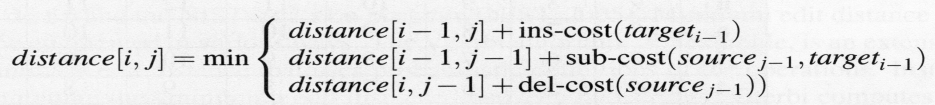
59.Використання динамічного програмування для визначення мінімального шляху вирівнювання.
Для визначення послідовності операцій необхідних для переходу від одного слова до іншого потрібно знайти найдешевший шлях від першої [0,0] клітинки матриці до останньої [i,j]. Як видно з прикладу існує декілька еквівалентних шляхів і алгоритм не тільки вираховує мінімальну відстань але й усі шляхи, використовуючи у кожному наступному кроці інформацію здобуту у попередніх кроках (принцип динамічного програмування).
60.Поняття n-грам моделі.
n-грам модель – імовірнісна модель, яка передбачає наступне слово на основі n-1 попередніх слів
• n-грам послідовність n слів
• 2-грам –біграм
• 3-грам - триграм
n-грам модель – це модель яка визначає (обраховує ) останнє слово n-грама на основі n-1 попередніх слів
