Глава 3. элементы аналитической геометрии 3 страница

Пример 7. Доказать, что прямые:

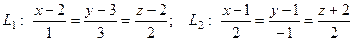скрещиваются и найти расстояние между ними.

Если прямые скрещиваются, то .

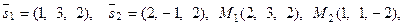вектор .

Следовательно, прямые скрещиваются. Найдём расстояние между ними. Для этого найдём ещё:

.

Тогда

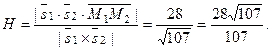
В заключение, решим ещё один пример.

Пример 8. Найти точку 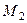, симметричную данной точке 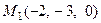относительно плоскости: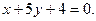

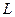С этой целью, запишем уравнение прямой , перпендику- лярной данной плоскости, проходящей через точку 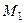. Её направляющий вектор можем считать равным нормальному вектору заданной плоскости, т.е. 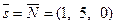. Тогда уравнения этой прямой имеют вид:

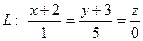, или её параметрические уравнения:

Найдём точку пересечения данной прямой с исходной плоскостью, т.е. найдём значение параметра в точке пересечения:

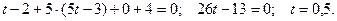
Тогда точка пересечения прямой и плоскости имеет коорди- наты: . Точку, симметричную точке 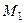от- носительно плоскости можно найти из того условия, что точка - середина отрезка . Следовательно,

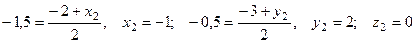
и, таким образом,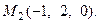

P

§ 6. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ.

Общее уравнение линии 2 – го порядка на плоскости имеет вид:

(1)

Для анализа этого уравнения нам понадобится понятие пре- образования координат на плоскости.

1. Параллельный перенос: пусть 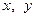- старые координа- ты, а 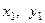- новые координаты, полученные переносом на- чала координат из точки в точку .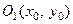

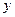
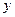
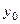
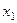
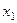
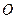
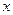
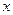
Для произвольной точки 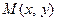получим

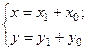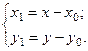(2) и (3)

(2) - это формулы перехода от старых координат к новым, (3) - формулы обратного перехода. Параллельный позволяет убрать в уравнении (1) линейные слагаемые (т.е. слагаемые ).

2. Поворот осей координат на угол .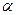

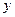
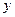
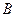
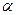
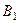
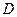
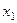
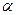
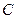
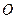
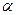
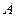
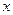
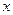
Из построения видно, что

Таким образом, получены формулы перехода от старых коор -динат к новым:

(4)

Аналогичным образом можно получить формулы обратного перехода от новых координат к старым при повороте системы координат:

(5)

С помощью поворота системы координат избавляются от произведения 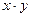в уравнении (1).

После преобразования уравнения (1) с помощью переноса и поворота системы координат, можем получить следующие уравнения: , или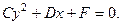

Рассмотрим сначала уравнение :

1. Если 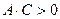, то имеем уравнение эллиптического типа, причём, в случае 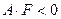, уравнение определяет эллипс (или окружность при 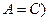; если же 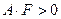, то уравнение определяет мнимый эллипс ( или мнимую окружность); если , то данное определение задаёт точку.

2. Если 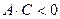, то имеем уравнение гиперболического ти- па, при этом, если 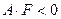, уравнение определяет гипербо- лу, если 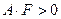- сопряжённую гиперболу, если , то уравнение определяет две скрещивающиеся прямые.

Уравнения вида параболического типа. Определяют либо параболы, направленные или по оси 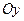, или по оси , либо две параллелельные прямые (если , то прямые параллельны оси 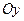; если - то прямые параллельны оси ).

Рассмотрим теперь основные линии 2 – го порядка.

1. Окружность - это геометрическое место точек равноу-

далённых от данной точки, называемой её центром. Не име- ет смысла подробно останавливаться на рассмотрении этой линии, так как её уравнения хорошо известны из школьного курса математики: - окружность с центром в начале координат, или смещённая окружность с центром в точке : .

2. Эллипс. Эллипсом называется геометрическое место то-

чек, для которых сумма расстояний до двух заданных точек, называемых фокусами, величина постоянная, большая, чем расстояние между фокусами.

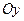Введём систему координат следующим образом: пусть ось проходит через фокусы данной линии, а ось делит отрезок 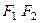пополам и перпендикулярна оси .

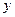
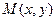
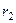
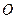
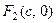
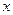
фокусы, расстояние между ними 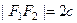, Тогда, по определению, Запишем данное равенство, используя формулу расстояния между точками:

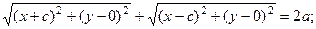
Правую и левую часть равенства возведём в квадрат и раскроем скобки:

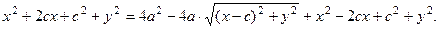После преобразования имеем Возводя полученное равенство в квадрат, получаем:

или .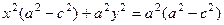

По определению, . Тогда существует единственное число , такое что 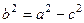. Получаем: . Окончательно, равенство:

(6) определяет каноническое уравнение эллипса.

Ввиду того, что переменные 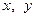входят в уравнение во второй степени, эта линия симметрична относительно осей ко- ординат. Следовательно, достаточно построить график в первой четверти ( ) и симмет- рично отобразить его в другие координатные плоскости. Оче- видно, что , . Построим линию:

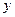
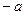
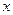
Величины и называются большой и малойполуоями эллипса, при этом расстояние от начала координат до фокусов равно . Величина 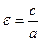называется эксцентриситетом и характеризует вытянутость эллипса. Для эллипса . В случае 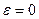, эллипс превращается в окружность.

Может оказаться, что , и тогда большая полуось - это . В этом случае, , эксцентриситет и, так как фокусы всегда находятся на больших полуосях, то они имеют следующие координаты: . Получаем следующий рисунок.

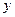
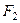
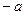
Оптическое свойство эллипса. Если источник света поме-щён в один из фокусов эллипса, то отражённый луч попадает в другой фокус.

Рассмотрим пример. привести уравнение линии к каноничес- кому виду и построить эту линию: .

Сгруппируем переменные и выделим полные квадраты:

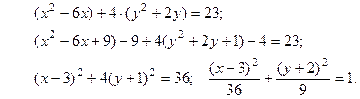
Получили каноническое уравнение эллипса в смещённой сис- теме координат 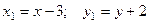, начало отсчёта кото –рой имеет координаты: : . Полуоси этого эллипса: .

Тогда её эксцентриситет . Построим линию.

O 2 x

-6 6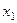

-3

3. Гипербола. Гиперболой называется геометрическое мес- то точек, для которых модуль разности расстояний до двух точек, называемых фокусами, величина постоянная, меньшая, чем расстояние между фокусами.

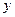
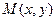
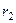
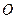
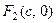
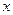
По определению, 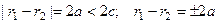. Тогда

Возведём это равенство в квадрат:

Раскроем скобки и изолируем корень:

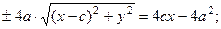
Возведём в квадрат полученное равенство и раскроем скобки:

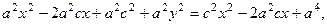
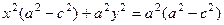. Но, по определению гипер- болы, и получается:

. Разделив это равенство на правую часть, получаем каноническое уравнение гиперболы:

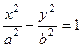. (7)

Ввиду того, что переменные 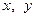входят в уравнение во второй степени, эта линия симметрична относительно осей ко- ординат и относительно начала координат. Следавательно, достаточно построить график 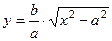в первой чет- верти ( ) и симметрично отобразить его в другие координатные плоскости. Из данного уравнения видим, что оно имеет смысл только в случае, если 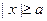. 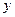возрастает по мере увеличения 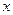и причём график линии по мере увели- чения 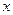приближается к прямой , не пересекая эту прямую. Эта прямая является асимптотой данной линии.

Ввиду симметрии, гипербола имеет две асимптоты: . Построим гиперболу:

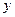
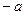
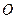
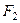
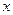
Асимптоты гиперболы - это прямые, проходящие через диаго -нали основного прямоугольника со сторонами, раными и , соответственно.

В уравнении (7), называется действительной полуосью ги- перболы, - мнимой полуосью. В результате преобразований уравнения второго порядка мы можем получить также уравне- ние следующего вида:

(8)

Оно задаёт уравнение сопряжённой гиперболы, которая выгля- дит следующим образом:

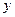
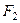
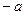
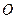
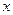
Для сопряжённой гиперболы - мнимая полуось, - действительная полуось. Сопряжённая гипербола имеет те же асимптоты . Как для случая гиперболы, так и для случая сопряжённой гиперболы, полуфокусное расстояние равно :

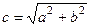. Для случая гиперболы, фокусы имеют коорди –наты: , для случая сопряжённой гиперболы: