Метод вращений решения полной проблемы собственных значений

Метод вращений предназначен для решения полной проблемы собств. знач. для эрмитовых матриц. В алгебре доказывается, что для эрмитовой матрицы 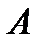существует унитарная матрица 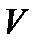, такая, что преобр. подобия с ней приводит матрицу 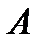к диагональной матрице 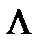: 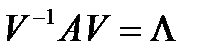(1)

Для унитарной матрицы по определению сопряженная матрица равна обратной: 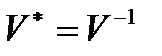. Т.о., равенство (1) можно переписать в виде 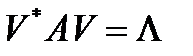(2)

Собств. знач. диагональной матрицы 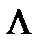явл. ее диагональные элем. 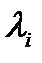, а собств. векторами – соотв. единичные (корд.) векторы 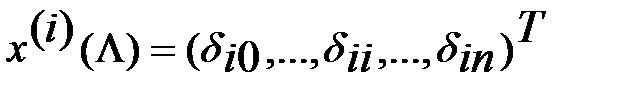, где 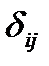- символ Кронекера. Выполнение равенств 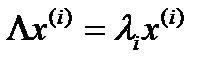в данном случае очевидно.

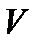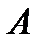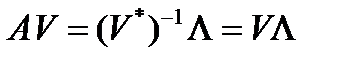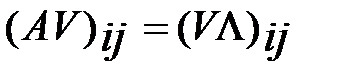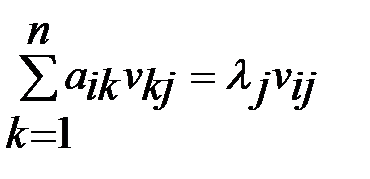Строки унитарной матрицы явл. собств. векторами матрицы . Это следует из (2): . Действительно, отсюда имеем или или 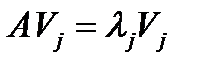, где .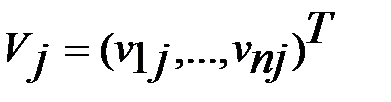

Вещественные симметрические матрицы явл. частным случаем эрмитовых матриц. Рассм. метод вращений для вещественных симметрических матриц.

Найдем наибольший по модулю внедиагональный элемент вещественной симметрической матрицы 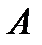. Пусть таковым оказался элемент 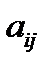.Без ограничения общности можно считать .

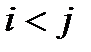Введем в рассм. матрицу вращения

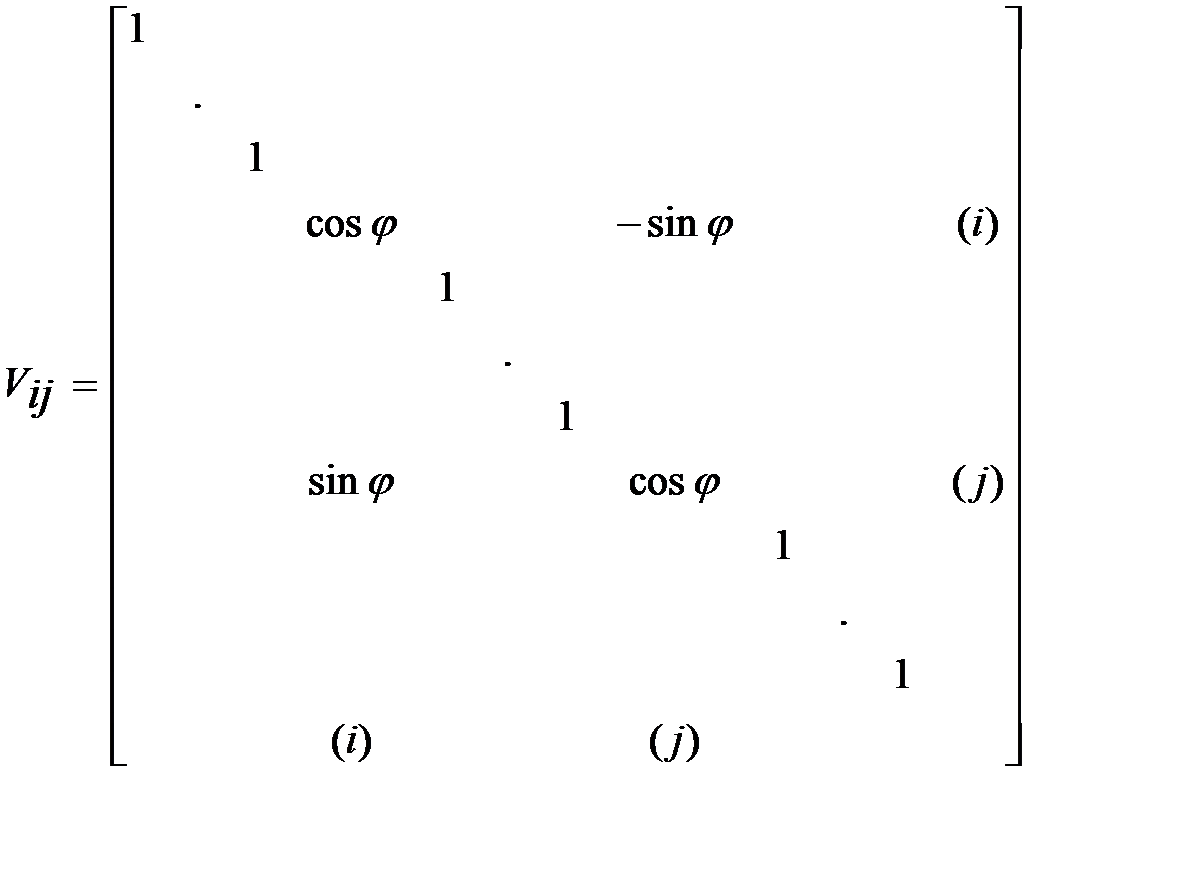
Умножим матрицу 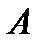справа на матрицу 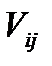. Получим матрицу 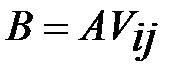, кот. отличается от матрицы 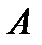только столбцами i и j:

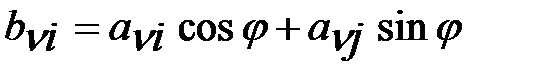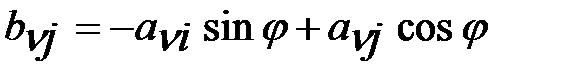(3), (4)

Из (3) и (4) при этом следует, что сумма квадратов элем. этих столбцов остается без изменения:

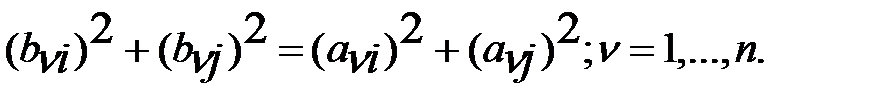(5)

Умножим матрицу 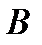слева на матрицу 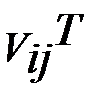. Получим матрицу 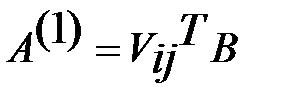, кот. отличается от матрицы 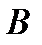только строками i и j:

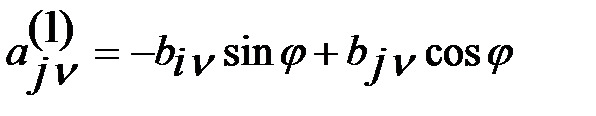(6), (7)

Из (6) и (7) при этом следует, что сумма квадратов элем. этих строк остается без изменения:

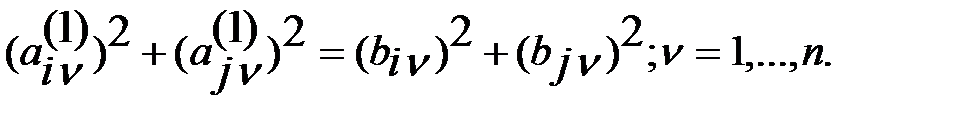(8)

Т.о., преобр. подобия 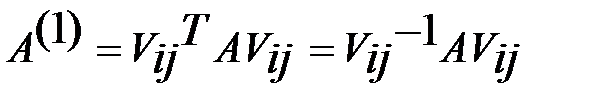(9) не меняет суммы квадратов элементов матрицы: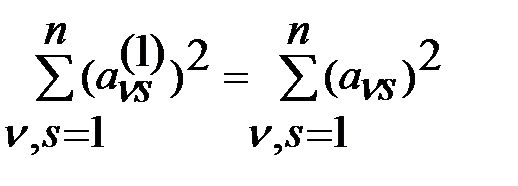

Преобр. подобия (9) также сохраняет симметричность матрицы: .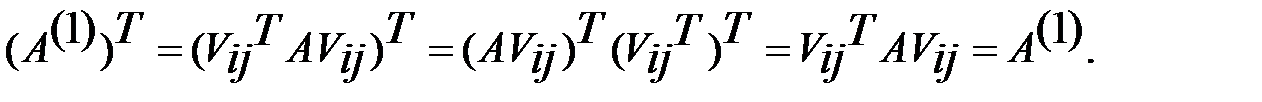

Теперь начинается самое главное. Преобр. подобия (9) меняет только два диагональных элемента. При этом, из симметрии , формул (8) и (5) следует: 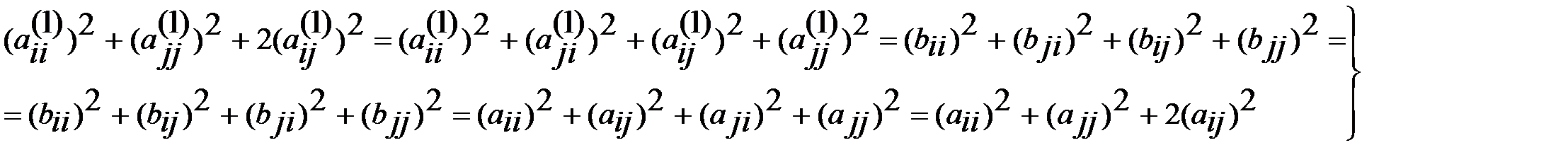Это значит, что при 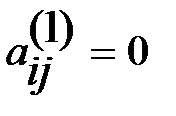преобр. (9) увеличит сумму квадратов диагон. элем. и соотв. уменьшит сумму квадратов внедиагон. элем. матрицы на величину 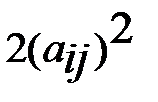. Из (6) и (4) получаем ур. для определ. соотв. угла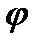

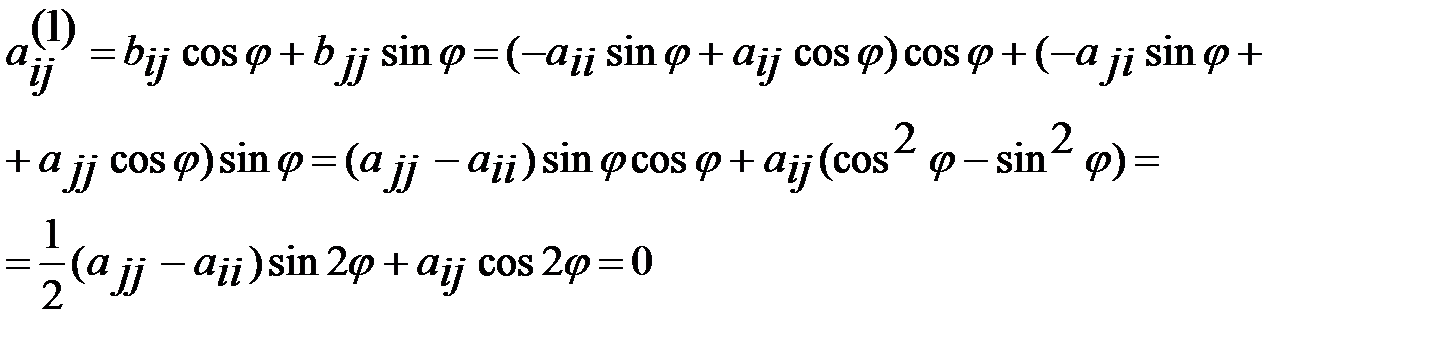
Отсюда находим искомый угол поворота 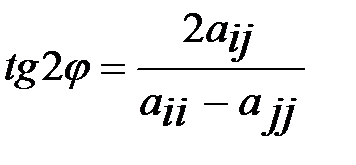, 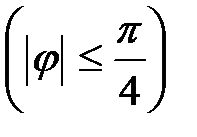(10)

Мы рассм. идею метода вращений и получили расчетные форм. метода. В методе вращений строится последовательность матриц 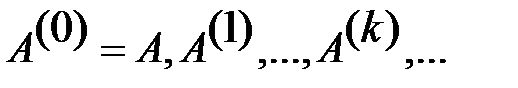(11)

по правилу 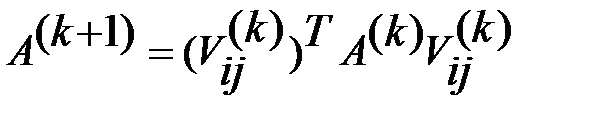(12)

Построение последов. (11) заканчивается получением матрицы 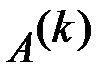, недиагон. элем. кот. можно считать равными нулю в пределах заданной точности. При этом ее диагон. элем. принимаются за собств. знач.

В качестве собств. векторов можно взять соотв. строки матрицы 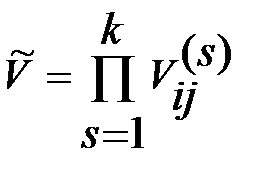. Может оказаться, что собств. векторы проще находить непосредственно решением сист. .

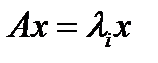Теорема. Матричная последов. (11) в методе вращений сходится к диагон. матрице со скоростью геометрической погрешности.

Доказательство. Обозначим 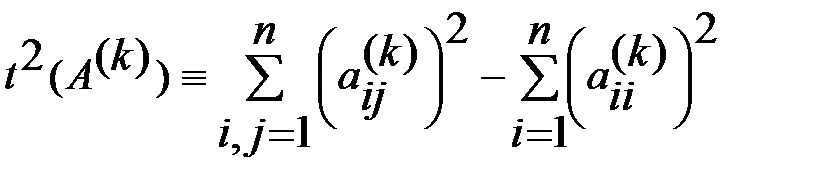. Имеем 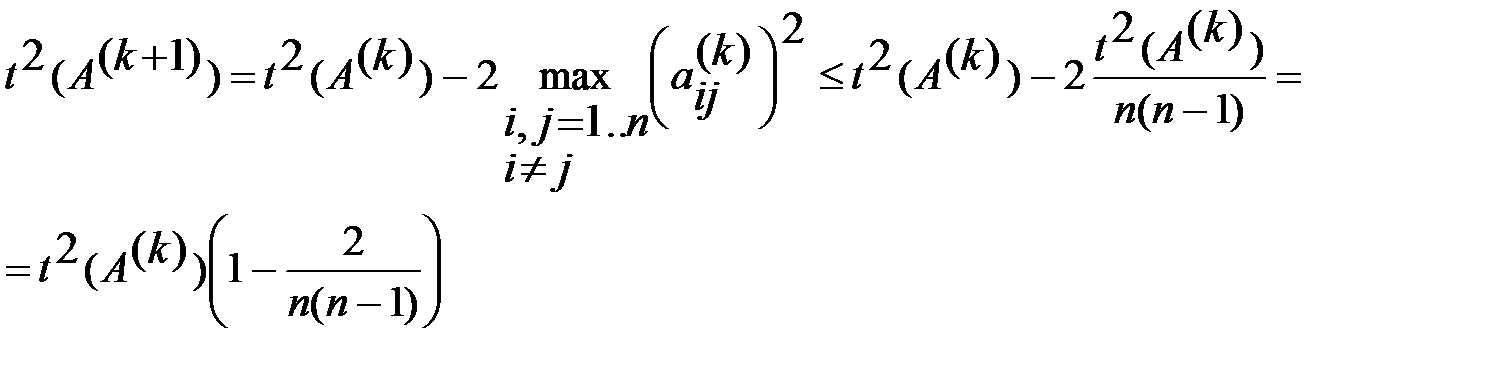Следовательно, сумма квадратов недиагон. элем. в матричной последов. (11) сходится к нулю не хуже, чем геометрическая последов. со знаменателем .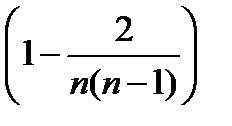