Принцип Даламбера для материальной точки и системы.

При движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю (уравновешенную систему сил) 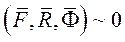В соответствии с аксиомами статики основное уравнение движения материальной точки имеет вид 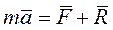, 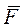- равнодействующая активных сил, 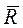- равнодействующая реакций связей. Запишем уравнение в виде 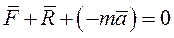Слагаемое 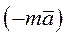обозначают 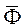и называют даламберовой силой инерции (или просто силой инерции). 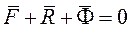При движении механической системы в любой момент времени приложенные силы и реакции связей вместе с силами инерции образуют систему сил, эквивалентную нулю.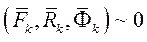 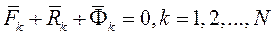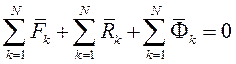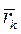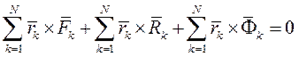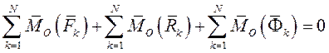Суммируя левые части по всем точкам Умножив каждое уравнение векторно слева на радиус-вектор k-й точки и просуммировав их, имеем: или Если силы, приложенные к k-й точке системы, разложить на внешнюю и внутреннюю, а не на активные и реакции связей, то 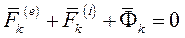Так как главный вектор и главный момент относительно произвольного центра приведения внутренних сил системы равен нулю, то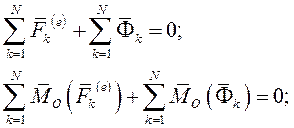
2)Принцип Даламбера для твердого тела. Определение главного вектора и главного момента даламберовых сил инерции для твердого тела. Статическая и динамическая балансировки.

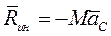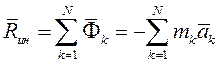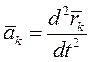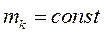
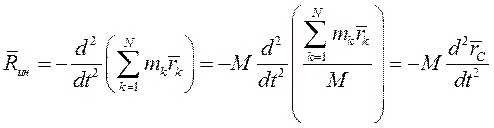
При любом движении механической системы главный вектор сил инерции равен взятому со знаком «минус» произведению массы системы В соответствии с определением главного вектора запишем Так как ускорение точки , а её масса 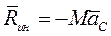Главный момент сил инерции относительно центра приведения О равен взятой со знаком «минус» производной по времени от главного момента количеств движения механической системы относительно того же центра.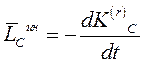

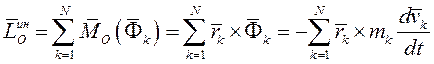
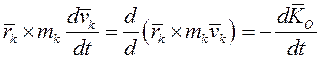
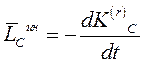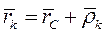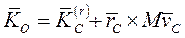Так как Если движение точек мех. системы рассматривать как сложное, т.е. , то Где 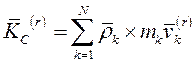- главный момент количеств движения системы в её относительном движении по отношению к системе координат, движущейся вместе с центром масс. В этом случае главный момент сил инерции относительно неподвижного центра приведения О 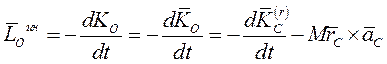Главный момент сил инерции относительно центра масс С 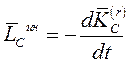При приведении сил инерции точек тела, вращающегося вокруг неподвижной оси, к произвольному центру О, расположенному на этой оси, в центре О в общем случае должны быть приложены главный вектор 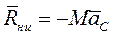и главный момент 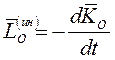сил инерции. Для уравновешивания деталей их подвергают балансировке. Существуют два вида балансировки: статическая и динамическая. 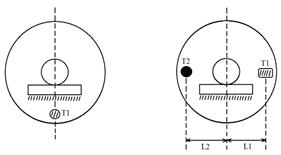Рис. 1. Схема статического уравновешивания деталей: Т1 — масса неуравновешенной детали; Т2 — масса уравновешивающего груза;L1, L2 — их расстояния от оси вращения. Статическая балансировка. У неуравновешенной детали ее масса располагается несимметрично относительно оси вращения. Поэтому при статическом положении такой детали, т. е. когда она находится в покое, центр тяжести будет стремиться занять нижнее положение (рис.1). Для уравновешивания детали добавляют с диаметрально противоположной стороны груз массой Т2 с таким расчетом, чтобы его момент Т2L2 был равен моменту неуравновешенной массы Т1L1. При этом условии деталь будет находиться в равновесии при любом положении, так как центр тяжести ее будет лежать на оси вращения. Равновесие может быть достигнуто также путем удаления части металла детали высверловкой, спиливанием или фрезерованием со стороны неуравновешенной массы Т1. На чертежах деталей и в Правилах ремонта на балансировку деталей дается допуск, который называют дисбалансом (г/см).Статической балансировке подвергают плоские детали, имеющие небольшое отношение длины к диаметру: зубчатое колесо тягового редуктора, крыльчатку вентилятора холодильника и т.п. Статическая балансировка ведется на горизонтально-параллельных призмах, цилиндрических стержнях или на роликовых опорах. Поверхности призм, стержней и роликов должны быть тщательно обработаны. Точность статической балансировки во многом зависит от состояния поверхностей этих деталей. Динамическая балансировка. Динамической балансировке обычно подвергают детали, длина которых равна или больше их диаметра. На рис. 2 показан статически отбалансированный ротор, у которого масса Т уравновешена грузом массой М. Этот ротор при медленном вращении будет находиться в равновесии в любом положении. Однако при быстром его вращении возникнут две равные, но противоположно направленные центробежные силы F1 и F2. При этом образуется момент FJU который стремится повернуть ось ротора на некоторый угол вокруг его центра тяжести, т.е. наблюдается динамическое неравновесие ротора со всеми вытекающими отсюда последствиями (вибрация, неравномерный износ и т. п.). Момент этой пары сил может быть уравновешен только другой парой сил, действующей в той же плоскости и создающей равный противодействующий момент. Для этого в нашем примере нужно приложить к ротору в той же плоскости (вертикальной) два груза массами Шх = т2 на равном расстоянии от оси вращения. Грузы и их расстояния от оси вращения подбирают так, чтобы центробежные силы от этих грузов создавали момент /уь противодействующий моменту FJi и уравновешивающий его. Чаще всего уравновешивающие грузы прикрепляют к торцовым плоскостям деталей или с этих плоскостей удаляют часть металла.
3)Механические связи и их классификация.

Связи – материальные тела, осуществляющие ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах. Чо не поймешь?! Эти ограничения записываются в виде уравнений или ограничений. Уравнения связей – уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени). Геометрические связи – связи, уравнения которых содержат только координаты точек механической системы. Эти связи выполнены в виде тел, поверхностей, линий и т. п. Например, связь в виде некоторой поверхности описывается уравнением f(X, Y, Z) = 0. Дифференциальные связи – связи, уравнения которых, кроме координат точек механической системы, содержат ещё первые производные от этих координат по времени. Уравнение такой связи имеет вид f(X, Y, Z, dX/dt, dY/dt, dZ/dt) = 0. Голономные связи – геометрические связи и дифференциальные связи, уравнения которых можно проинтегрировать. Неголономные связи – дифференциальные связи, уравнения которых не могут быть проинтегрированы. Стационарные связи – связи, в уравнения которых время явно не входит. Например, геометрическая стационарная связь в виде невесомого стержня длины l, ограничивающая перемещение материальной точки (рис. 6.11), описывается уравнением X² + Y² + Z² – l² = 0. Если в рассматриваемом примере (рис. 6.11) вместо стержня будет нить, длина которой с течением времени изменяется, то такая связь будет геометрически нестационарной. Эта связь описывается уравнением X² + Y² + Z² – l²(t) = 0. Двусторнние (удерживающие) связи – связи, допускающие возможные перемещения только в двух взаимно противоположных направлениях. Примером такого типа связи служит, например, кулисный камень. Эти связи описываются уравнением f(X, Y, Z, t) = 0. Односторонние (неудерживающие) связи – связи, при которых точки механической системы имеют возможные перемещения, противоположные которым не являются возможными. К связям такого типа относится, например, шарнирно-подвижная опора. Аналитически эти связи описываются неравенствами типа f(X, Y, Z, t) ≥ 0.
4)Принцип возможных перемещений в обычной форме и в обобщенных координатах.

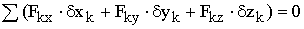Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю. или в проекциях: Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики. Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы. Тогда принцип возможных перемещений в обобщенных координатах будет выглядеть следующим образом: 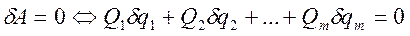А поскольку все обобщенные координаты независимы, то это может быть только тогда, когда 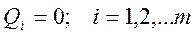Последнее выражение есть следствие, означающее: система находится в равновесии тогда и только тогда, когда все обобщенные силы равны нулю.
5)Обобщенная сила и три способа ее вычисления.

Обобщенной силой Q_i, соответствующей обобщенной координате q_j, называют скалярную величину, определяемую отношением элементарной работы действующих сил на перемещении механической системы, вызванном изменением обобщенной координаты q_j, к величине приращения этой координаты δq_j: Q_i = δA_j/δq_j или δA_j = Q_i⋅ δq_j. Размерность обобщенной силы зависит от размерности обобщенной координаты и может выражаться в единицах силы [Н], момента [Н∙м]. Число обобщенных сил для данной системы соответствует числу обобщенных координат. Первый способпредполагает прямое вычисление коэффициентов при вариациях обобщенных координат в выражении виртуальной работы. Удобнее здесь варьировать не все сразу обобщенные координаты, а по одной. Записывается выражение работы на виртуальном перемещении системы, отвечающем вариации только одной обобщенной координаты, например, с номером k — 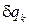, как алгебраическую сумму виртуальных работ активных сил, приложенных к телам и точкам механической системы 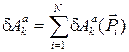. Затем, вынося за скобки общий сомножитель — вариацию обобщенной координаты 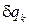, получим выражение для обобщенной силы 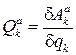Для системы с несколькими степенями свободы такую операцию следует проделать столько раз, сколько обобщенных координат.Второй способ основан на зависимостях типа, заданных в явном виде. Тогда обобщенные силы определятся выражением 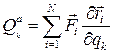, k=1,2,…,s. Третий способ опирается на знание потенциальной энергии системы как функции координат ее точек 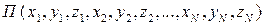. Подставляя в нее выражения (5.3), получим зависимость потенциальной энергии от обобщенных координат 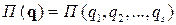, а виртуальная работа будет 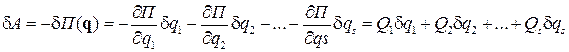Сравнивая коэффициенты при одинаковых вариациях, найдем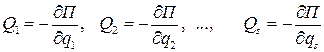
6)Запиши мне: общее уравнение динамики в обычной форме и в обобщенных координатах.

Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии. Следует отметить, что общее уравнение динамики можно применять и для систем с неидеальными связями, только в этом случае реакции неидеальных связей, таких, например, как сила трения или момент трения качения, необходимо отнести к категории активных сил. Работа на возможном перемещении как активных, так и сил инерций, ищется также как и элементарная работа на действительном перемещении: Возможная работа силы: Возможная работа момента (пары сил): Запишем выражение виртуальных работ активных сил и сил инерции механической системы и приравняем его нулю откуда, благодаря независимости вариаций обобщенных координат друг от друга, что имеет место для голономных систем, следует s уравнений или в другой форме, напоминающей II закон Ньютона Эти уравнения и являются уравнениями, описывающими динамическое поведение механической системы с голономными связями. Их можно применять непосредственно для вывода уравнений движения. 7)Уравнение Лагранжа 2-го рода.

Найдем слагаемое с номером i в правой части 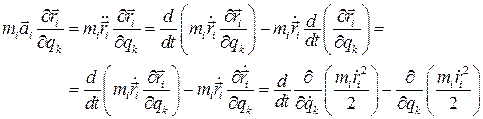Здесь использованы два тождества Лагранжа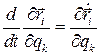 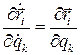После суммирования получим обобщенную силу инерции 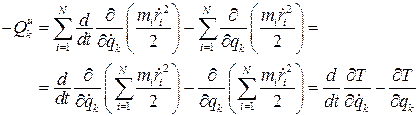Здесь величина 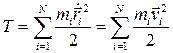, где 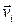-скорость i-ой точки, есть, очевидно, кинетическая энергия механической системы. Окончательно получим 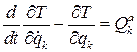, k=1,2,...,s, где s — число степеней свободы, 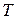— кинетическая энергия, 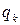, , 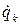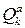- обобщенная координата, обобщенная скорость и обобщенная активная сила с порядковым номером 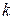данной механической системы.
8)Уравнение Лагранжа 2-го рода для консервативных систем.

Для консервативной механической системы обобщенные силы определяются через потенциальную энергию системы соотношениями: 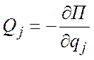Тогда уравнения Лагранжа перепишутся в виде 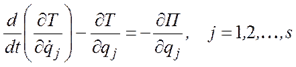Введем функцию Лагранжа 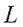соотношением: 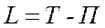. Учитывая, что потенциальная энергия есть функция только обобщенных координат 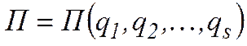, имеем 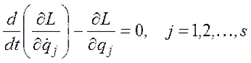Если в функцию Лагранжа не входят явно 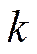обобщенных координат 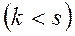, то возможно частичное интегрирование дифференциальных уравнений движения механической системы. Соответствующие обобщенные координаты называются циклическими. Для них 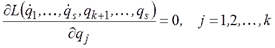Тогда 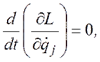откуда находим 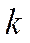общих интегралов системы дифференциальных уравнений движения механической системы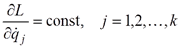
9)Первые интегралы уравнений Лагранжа 2-го рода (циклический интеграл, обобщенный интеграл энергии).

Л. у. 1го рода описывают движения как голономных систем, стесненных только геометрич. связями вида 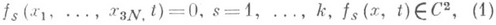так и неголономных систем, на которые наложены, помимо связей (1), кинематич. связи вида 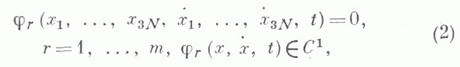где 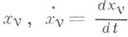- декартовы координаты и скорости точек, N - число точек системы, t - время,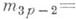 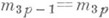- масса р_точки, имеющей координаты. Связи 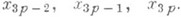(1) и(2) предполагаются независимыми, т. е. ранги матриц 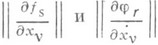равны соответственно kи т. Л. у. 1-го рода имеют вид

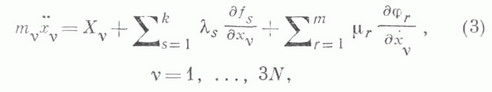где 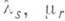- неопределенные множители Лагранжа, пропорциональные реакциям связей, 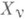- проекции наоси координат заданных активных сил, причем сила F_p действующая на р_точку, имеет проекции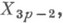 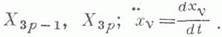К дифференциальным уравнениям (3) надлежит присоединить k+m уравнений (1) и (2), в результате чегополучается система 3N+k+т уравнений с таким же числом неизвестных 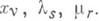Л. у. 1го рода напрактике обычно применяются для систем с небольшим числом неизвестных.Л. у. 2го рода описывают движения лишь голономных систем, стесненных связями вида (1). Введением врассмотрение n=3N-k независимых обобщенных лагранжевых координат q_i, с помощью к-рых любоевозможное положение системы может быть получено при нек-рых значениях q_i из равенств

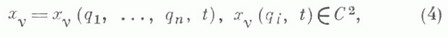обращающих уравнения (1) в тождества, устанавливается для каждого tвзаимно однозначное соответствиемежду возможными положениями системы и точками нек-рой области n-мерного конфигурационногопространства (q₁, .., q_n). В случае стационарных связей (1) всегда возможно выбрать переменные д;так, чтовремя tне будет входить в уравнения (4). Далее записываются с помощью уравнений (4) выражения длясуммы элементарных работ всех активных сил F_p на возможных перемещениях системы 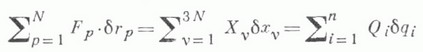и кинетич. энергии системы 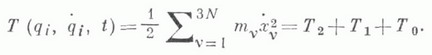Здесь

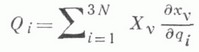- обобщенная сила, соответствующая координате 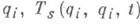- однородные степени s формыобобщенных скоростей q_i, причем 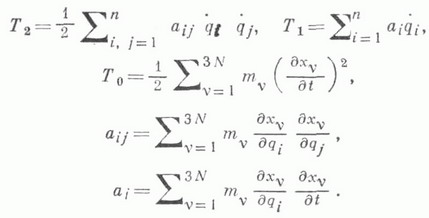В случае стационарных связей Т= Т ₂. Л. у. 2-го рода имеют вид 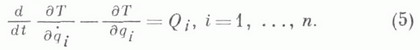Уравнения (5) представляют собой систему га обыкновенных дифференциальных уравнений 2-го порядка снеизвестными q_i. Они инвариантны по форме относительно выбора лагранжевых координат. Эта системауравнений движения имеет наименьший возможный порядок 2n. В этом, а также в отсутствии в уравнениях (5)реакций связей, состоит большое преимущество уравнений (5) по сравнению с Л. у. 1-го рода (3). Послеинтегрирования системы (5) реакции связей могут быть определены из уравнений, выражающих второй законНьютона для точек системы.В случае потенциальных обобщенных сил, когда существует силовая функция 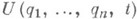такая, что 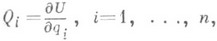уравнения (5) принимают вид

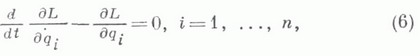где 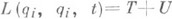носит название функции Лагранжа, или кинетич. потенциала. Если или - 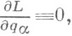то уравнения (6) допускают обобщенный интеграл энергии

или циклический интеграл блин!

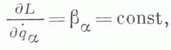соответствующий циклической координате q _а.
10)Функции кинетической и потенциальной энергий механической системы, выраженные через обобщенные координаты.

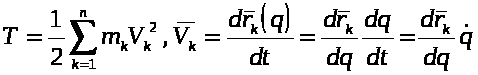
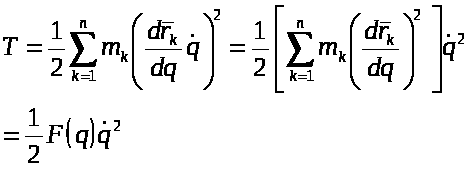
Выразим кинетическую энергию системы через обобщённые скорости и обобщённые координаты по формулам: 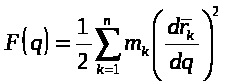Разложим функцию F(q) в ряд Тэйлора в окрестности точки q₀=0: 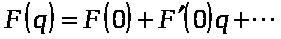Будем определять кинетическую энергию системы с точностью до квадратов малых величин 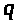и 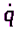. Тогда в разложении (5) следует сохранить только первое слагаемое F(0). В этом случае выражение кинетической энергии системы примет следующий вид: 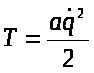, где 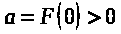Выражение кинетической энергии системы в случае её малых колебаний напоминает выражение кинетической энергии материальной точки, в котором скорость точки заменена обобщённой скоростью системы 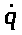, а масса точки заменена коэффициентом а, который, в данном случае, называется коэффициентом хинерции! Чо не поймешь?!. Разложим теперь потенциальную энергию системы П(q) в ряд Тэйлора в окрестности точки q₀=0, ограничивая его слагаемыми второго порядка малости и принимая во внимание равенства: 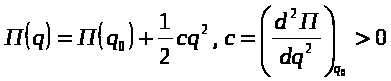Если потенциальную энергию в точке q₀ принять равной нулю, то выражение потенциальной энергии системы вблизи её устойчивого положения равновесия будет внешне похоже на выражение потенциальной энергии упругой или квазиупругой силы (см. Лекция 6, пункт 3, мелкий шрифт). Поэтому по аналогии с потенциалом упругой силы величина с называется квазиупругим коэффициентом или обобщённым коэффициентом жёсткости.
11)Функции Рэлея (функция рассеивания) и ее физический смысл.

Пусть на любую точку системы, имеющую 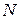степеней свободы, действует сила сопротивления пропорциональная первой степени скорости 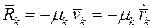,где 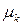— коэффициент сопротивления.Силе сопротивления 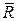сопоставляется диссипативная функция Рэлея 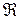, характеризующая быстроту рассеивания (диссипации) энергии системы 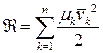,которую при стационарных связях 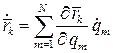можно представить следующим образом: 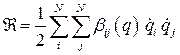, где 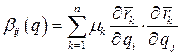Для системы с конечным числом степеней свободы, ограничиваясь в разложении коэффициентов в ряд Маклорена только первыми членами, получим выражение функции рассеивания Рэлея в виде однородной положительной квадратичной функции обобщённых скоростей 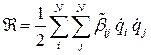, где 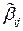— постоянные, называемые коэффициентами диссипации или приведёнными коэффициентами сопротивления.Отсюда для системы с одной степенью свободы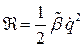
12)Теорема Лагранжа – Дирихле об устойчивости положения равновесия механической системы. Теорема Ляпунова и критерий Сильвестра (не Сталоне).

Если в положении равновесия консервативной механической системы с идеальными и стационарными связями потенциальная энергия имеет локальный минимум, то это положение равновесия устойчиво. Так как потенциальная энергия в положении устойчивого равновесия принимается равной нулю, и в этом положении она имеет локальный минимум, то вблизи положения равновесия 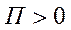, т.е. соответствующая квадратичная форма положительно определенная. Математическое условие положительной определенности любой квадратичной формы дается теоремой Сильвестра, доказываемой в курсах линейной алгебры: Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительными. В случае квадратичной формы для потенциальной энергии:

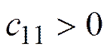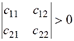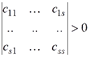, , …, .В частности, для системы с двумя степенями свободы 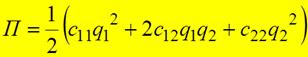и согласно теореме Сильвестра условие устойчивости имеет вид: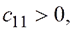

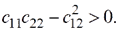
13)Устойчивость положения равновесия механической системы с «К» степенями свободы. (см. 14)

Необходимое условие 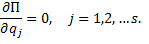Достаточное условие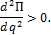
14, 15, 17)Свободные незатухающие (без сопротивления) колебания механической системы с одной степенью свободы, свободные затухающие (с сопротивлением) колебания механической системы с одной степенью свободы, вынужденные колебания механической системы с одной степенью свободы с сопротивлением.