Многошаговые методы. экстраполяционные формулы адамса

Способ определения частичных сумм ряда (8.4) без определения значения неизвестных по формулам (8.5) был предложен Адамсом. Пусть известно решение 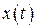уравнения (8.1) в точках (на сетке)

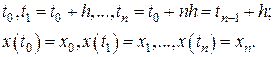
Воспользуемся разложением 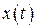в ряд Тейлора, имеем

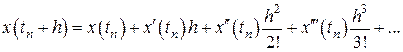
или

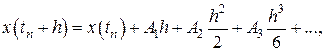(8.14)

где

.

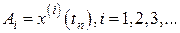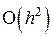Для получения требуемой локальной точности вычислений необходимо в ряде (8.14) учитывать соответствующее число членов. Учет слагаемого, содержащего дает остаточный член , т.е. имеет место погрешность порядка 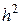. Учет члена, содержащего дает остаточный член 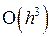, соответственно погрешность вычислений будет пропорциональна и т.д.

Коэффициенты 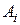можно выразить изначально при заданной точности вычислений через значения 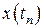и 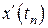при различных . Для этого продифференцируем (8.14) по 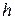. В результате получим

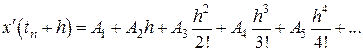. (8.15)

Левая часть выражения (8.15) представляет собой правую часть дифференциального уравнения (8.1) при 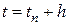, то есть

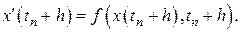
Обозначим

,

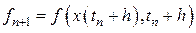тогда выражение (8.15) можно записать в виде

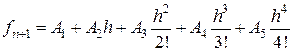. (8.16)

Из выражения (8.16) можно получить целую серию формул для определения 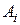. Для этого достаточно шагу интегрирования придавать определенные значения.

Пусть достаточно при вычислении иметь погрешность порядка 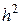. В этом случае необходимо знать только коэффициент . Для его нахождения положим 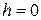, тогда из выражения (8.16) следует

.

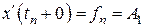Подставим коэффициент в формулу (8.14), получим

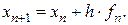
Это – известная формула Эйлера.

Если требуется точность порядка , необходимо знать два коэффициента и . Для их нахождения возьмем 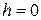и отрицательное значение 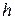. В результате получаем следующую систему уравнений для нахождения и :

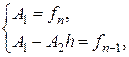
Следовательно

.

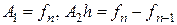Подставляя эти значения в формулу (8.14), получаем

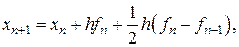
или

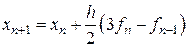. (8.17)

Формулу (8.17) называют формулой трапеций.

Для получения точности порядка 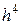необходимо знать коэффициенты 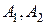и .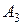

Придавая значения равные 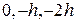, получаем следующую систему уравнений

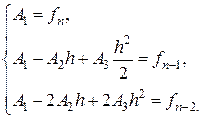
Имеем следующие значения для коэффициентов :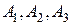

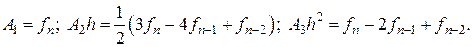
Подставив эти коэффициенты в формулу (8.14), получаем

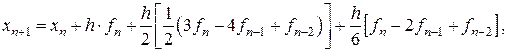
или

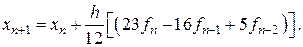(8.18)

По рассмотренному алгоритму можно получить формулы, обеспечивающие любую заданную локальную точность вычислений. Для погрешности пропорциональной имеет место вычислительная схема

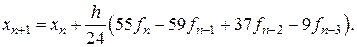(8.19)

Общий вид экстраполяционной формулы Адамса выраженной через конечные разности функции 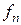имеет вид

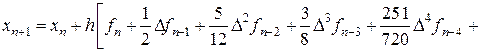
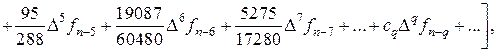(8.20)

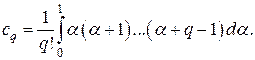
Здесь 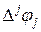– конечная разность порядка .

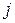Конечные разности находятся следующим образом. Пусть для равноотстоящих значений аргумента 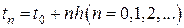известны соответствующие им значения функции .

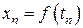Конечными разностями первого порядка называются величины

.

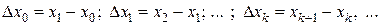Разности второго порядка определяются равенствами

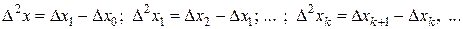
Разности порядка 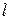определяются следующим образом:

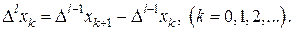
Вторые и последующие разности можно вычислить через значения самих функций в узловых точках:

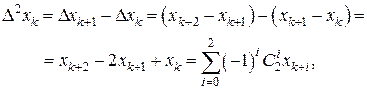
где

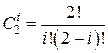– биномиальный коэффициент.

.

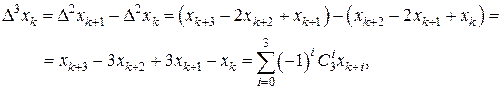
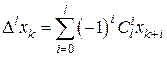Особенность формулы (8.20) в том, что ее можно обрывать на любом члене. Учет каждого дополнительного члена повышает точность вычислений на порядок.

Учет одного члена в квадратных скобках дает формулу Эйлера. Двух членов – формулу (8.17), трех членов – формулу (8.18) и т.д.

Вычислительный процесс по формулам Адамса требует определенной организации. Рассмотрим организацию вычислений на примере формулы (8.17).

Имеем

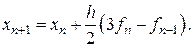
Очевидно, что формула справедлива только для .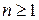

Для 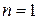имеем

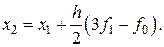
Для 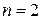имеем

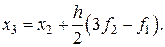
И так далее.

Для того, чтобы начать вычислительный процесс необходимо каким-то образом определить 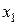. Для нахождения 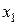обычно используется какой-либо одношаговый метод, имеющий туже точность. Вычислительная схема, реализуемая по формуле (8.17) имеет локальную точность порядка 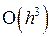. Для нахождения значения 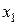и соответственно 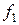можно использовать, например, метод Эйлера-Коши. Определив 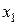и 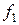, можно далее организовать вычислительный процесс по формуле (8.17).

Для организации вычислительного процесса, то есть заготовка начала таблицы значений решения дифференциального уравнения, можно воспользоваться простейшим методом Эйлера, но провести вычисления с шагом, меньшим, чем шаг интегрирования по схеме Адамса. Например, можно сделать шаг 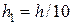( 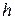– шаг интегрирования по схеме Адамса, 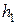– шага интегрирования по формуле Эйлера). В этом случае локальная погрешность формулы Эйлера по отношению к схеме Адамса будет .

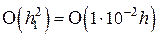Таким образом, необходимо сделать 10 шагов «заготовки» начала таблицы, то есть вычисление 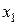и .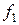

Примерная структурная схема алгоритма решения дифференциального уравнения (8.1) по схеме Адамса (8.17) при использовании в качестве «разгонного» метода трапеций приведена на рис. 8.1.

При организации вычислений по схеме Адамса, обеспечивающих более высокую локальную точность, необходимо предварительно «заготовить» большое число начальных значений таблицы вычислений, используя в качестве «разгонного» одношаговый метод. И только после этого реализовывать схему Адамса.