Решение типовых задач по построению эпюр перерезывающих сил и изгибающих моментов. Задания для индивидуальной работы
Пример 8.6.1. Построить эпюры перерезывающих сил  и изгибающих моментов М для балки, испытывающей поперечный изгиб и показанной на рис. 8.18:
и изгибающих моментов М для балки, испытывающей поперечный изгиб и показанной на рис. 8.18: 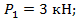 .
. 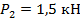 ;
; 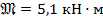 ;
; 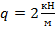 ;
; 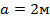 ;
; 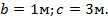
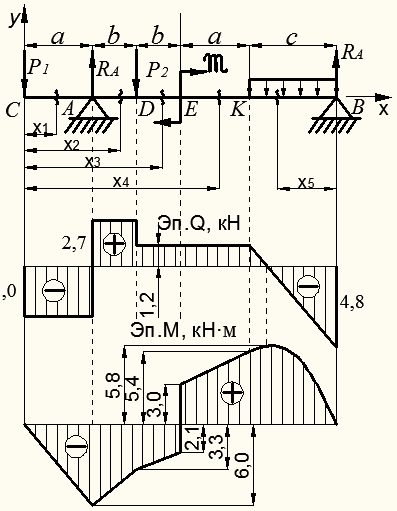
Рисунок 8.18 – Построение эпюр  и М для шарнирно-опертой балки
и М для шарнирно-опертой балки
Решение
1. Определим опорные реакции из условий статики:
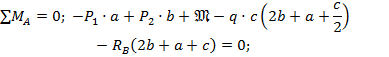
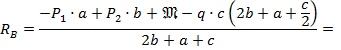


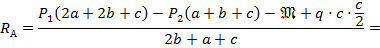

Проверка: 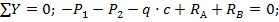
 реакции найдены верно.
реакции найдены верно.
2. Разбиваем балку на 5 участков (см. рис.8.18): СА, АD, DE, ЕК, КВ. Начало координат принимаем в левом сечении балки т. С.
3. Определяем значения  и М на каждом участке:
и М на каждом участке:
Участок СА: 
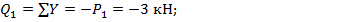
Откладываем постоянную ординату  на участке СА;
на участке СА; 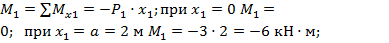 поскольку
поскольку 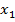 входит в выражение для
входит в выражение для 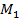 в первой степени, то закон изменения
в первой степени, то закон изменения 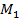 на участке линейный: откладываем ординаты
на участке линейный: откладываем ординаты 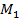 в начале и конце участка.
в начале и конце участка.
Участок АD: 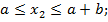

откладываем постоянную ординату 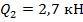 на участке;
на участке;
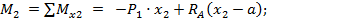
при 
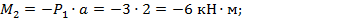
при 
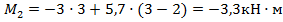 ;
;
откладываем ординаты эп. М на участке.
Участок DE: 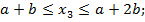

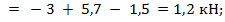 откладываем постоянную ординату
откладываем постоянную ординату  на участке;
на участке;

 ;
;
при_ 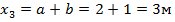
 ) –
) –
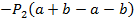 =
=
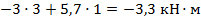 ;
;

 1
1

откладываем ординаты эп. М на участке.
Участок ЕК: 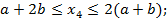
 продолжаем на участке эп.
продолжаем на участке эп.  прежнюю ординату;
прежнюю ординату;


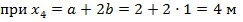
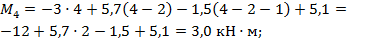

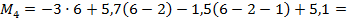


откладываем ординаты эп. М на участке.
Участок КВ: из-за более громоздких вычислений проще откладывать координату  с правого конца балки т.В:
с правого конца балки т.В: 
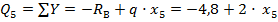
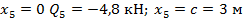
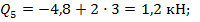
откладываем ординаты эп. 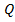 на участке КВ, учитывая линейный закон изменения перерезывающей силы;
на участке КВ, учитывая линейный закон изменения перерезывающей силы;
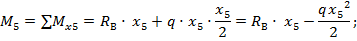
из полученной зависимости видно, что координата  во второй степени и закон изменения
во второй степени и закон изменения  на участке отвечает квадратичной параболе; ординаты изгибающего момента на участке следующие: при
на участке отвечает квадратичной параболе; ординаты изгибающего момента на участке следующие: при 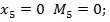 при
при 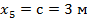 ,
, 
Найдем максимум изгибающего момента на участке КВ, учитывая, что 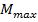 соответствует координате х на участке, где
соответствует координате х на участке, где 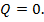 Приравняем уравнение для
Приравняем уравнение для 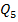 нулю и найдем из него координату
нулю и найдем из него координату  , где
, где  откуда
откуда  для участка КВ. Тогда
для участка КВ. Тогда 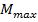 на этом участке при
на этом участке при 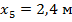 равен
равен 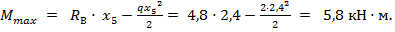 Откладываем полученные ординаты эп. М на участке.
Откладываем полученные ординаты эп. М на участке.
Обращаем внимание на то, что выпуклость эп._М направлена навстречу интенсивности внешней нагрузки q.
В итоге строим эп.  и эп. М на участке.
и эп. М на участке.
Окончательно полученные эпюры перерезывающих сил и изгибающих моментов для балки показаны на рис. 8.18.
Эпюры необходимы для определения опасных сечений балки, где действуют максимальные по модулю значения внутренних силовых факторов: 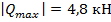 ;
; 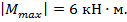
Отметим также, что в сечениях балки, где  и М меняют знаки, значения этих силовых факторов соответствуют величинам слева и справа от сечения, а не значениям
и М меняют знаки, значения этих силовых факторов соответствуют величинам слева и справа от сечения, а не значениям  и М в этом сечении по модулю (например в сечении
и М в этом сечении по модулю (например в сечении  по рис.8.19 значение М слева от сечения равно (-2,1 кН·м), справа – (+3,0 кН·м)), но не
по рис.8.19 значение М слева от сечения равно (-2,1 кН·м), справа – (+3,0 кН·м)), но не 
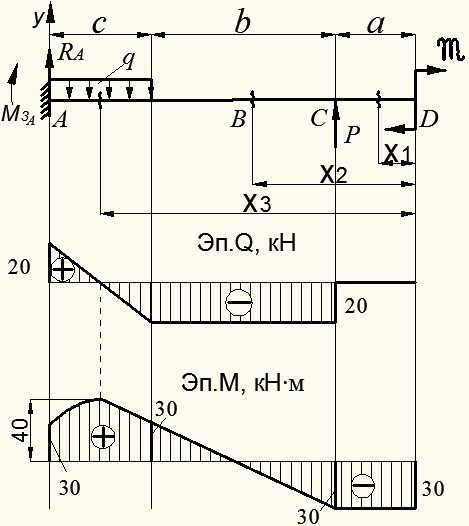 Пример 8.6.2. Построить эпюры перерезывающих сил и изгибающих моментов для балки, показанной на рис.8.19, при следующих исходных данных:
Пример 8.6.2. Построить эпюры перерезывающих сил и изгибающих моментов для балки, показанной на рис.8.19, при следующих исходных данных: 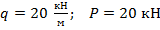 ;
;  ;
; 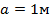 ;
; 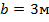 ;
; 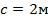 .
.
Рисунок 8.19 – Построение эпюр 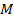 и и 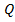 для консольной бакли для консольной бакли |
Решение
Решение
Для консольной балки определение опорных реакций 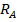 и
и  можно не проводить в случае отсчета координаты х от правого конца балки; они получаются автоматически после построения эпюр.
можно не проводить в случае отсчета координаты х от правого конца балки; они получаются автоматически после построения эпюр.
Участками балки при построении эпюр будут: АВ, ВС и СD.
1. Построение эпюры перерезывающих сил. На первом участке СD (сечение 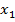 ) перерезывающих сил нет. На эпюре
) перерезывающих сил нет. На эпюре  этому соответствует прямая линия с нулевой координатой, совпадающая с осью эпюры.
этому соответствует прямая линия с нулевой координатой, совпадающая с осью эпюры.
На втором участке ВС (сечение 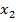 ) перерезывающая сила с учетом правила знаков равна:
) перерезывающая сила с учетом правила знаков равна:

На третьем участке АВ перерезывающая сила определяется зависимостью:
 Из данного выражения видно, что перерезывающая сила изменяется по линейному закону.
Из данного выражения видно, что перерезывающая сила изменяется по линейному закону.
Координата 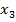 на участке лежит в пределах:
на участке лежит в пределах:
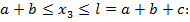
- при 

- при 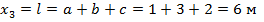

Откладываем ординаты перерезывающей силы на этом участке и получаем в итоге эп.  для всей балки; из эпюры получаем
для всей балки; из эпюры получаем  .
.
Построение эпюры изгибающих моментов. На первом участке балки СD изгибающий момент постоянен и с учетом правила знаков 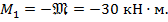 Откладываем это значение изгибающего момента по участку на эп. М.
Откладываем это значение изгибающего момента по участку на эп. М.
На втором участке ВС изгибающий момент равен:
 и изменяется по закону прямой.
и изменяется по закону прямой.
Для построения эпюры на участке 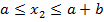 найдем два значения моментов:
найдем два значения моментов:
-_при 
-_при 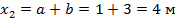
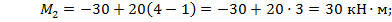
Ординаты эпюры 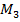 откладываем на участке и соединяем прямой.
откладываем на участке и соединяем прямой.
На третьем участке АВ  изгибающий момент равен:
изгибающий момент равен:
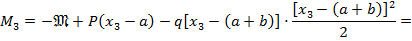
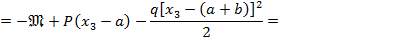
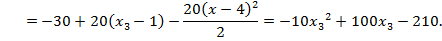
На этом участке график изгибающего момента имеет вид квадратичной параболы, поэтому вначале при построении эпюры найдем значения 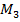 на границах участка:
на границах участка:
- при 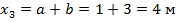
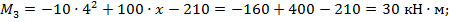
- при 
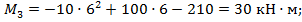
Из эпюры получаем значения реактивного момента в заделке т. А: 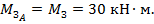
Максимум квадратичной параболы изменения 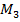 на участке соответствует точке эп.
на участке соответствует точке эп. 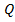 , где
, где 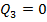 . Поэтому значение максимального момента
. Поэтому значение максимального момента 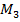 при
при  равно:
равно:
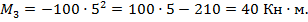
Откладываем значения трех моментов на участке СD и окончательно получаем эпюру изгибающих моментов для балки (см. рис. 8.2). Из эпюр  и
и 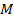 получаем:
получаем: 
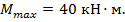
 Эти значения используются в дальнейшем при расчете нормальных и касательных напряжений в опасных сечениях для проверки прочности балки.
Эти значения используются в дальнейшем при расчете нормальных и касательных напряжений в опасных сечениях для проверки прочности балки.
