Тема урока. Решение задач на движение в одном направлении.
Цели урока:1)показать приемы поиска решения задач на движение в одном направлении;
2) закрепить алгоритм умножения многозначного числа на однозначное.
3) развивать навык устных и письменных вычислений;
4) снижать уровень тревожности на уроке;
5 )воспитывать интерес к урокам математики
Ход урока
1.Организационный момент
2. Проверка домашнего задания
3. Устный счёт
4.Работа по учебнику
(У) Задания9, 2, 4, 5*.
Задание2.Ученики вспоминают правило: чтобы определить количество десятков в числе, надо справа закрыть одну цифру, чтобы определить количество сотен — нужно закрыть две цифры.
Задание 5*. Ученики должны догадаться: чтобы число делилось на 2 и на 3, нужно, чтобы оно делилось на 6. Среди чисел 1, 2, 3, 4, ..., 48, 49, 50 делятся на 6 числа 6, 12, 18, 24, 30, 36, 42, 48 — всего 8 чисел.
Задание 9. На доске рисуется чертеж.
 |
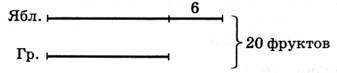Ответ: 7 груш и 13 яблок.
5.Работа в тетрадях
(П) Задания 1, 3, 7, 6, 8.
Задание 1. Сначала анализируется рисунок: поезда двигаются в одном направлении; второй поезд едет с большей скоростью, чем первый; расстояние между поездами уменьшается (сокращается), они сближаются. Может ли второй поезд догнать первый? (Может, потому что он едет быстрее, чем первый.)
Дальше анализируется таблица. Когда второй поезд стал двигаться, первый прошел уже 120 км; расстояние между поездами было первоначально 120 км. Потом расстояние стало сокращаться: 120 км, 90 км, 60 км, 30 км, 0 — за каждый час расстояние сокращается на 30 км. Через 4 ч после выезда второй поезд догонит первый; расстояние между ними будет равно 0. За это время поезда отдалятся от города на 360 км.
После этого оформляется решение:
1) 90 - 60 = 30 (км/ч) — скорость сближения поездов;
2) 120 : 30 = 4 (ч) — понадобится, чтобы второй поезд догнал первый;
3) 90 • 4 = 360 (км) или 60 • 6 = 360 (км) - расстояние от города.
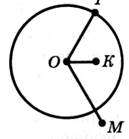Задание 7.
ОР = 20 мм;
ОК < 20 мм;
ОМ > 20 мм;
ОК<ОР< ОМ.
Физкультминутка
Задание 8.
а) Можно ответить на вопрос, сделав определенные вычисления: (х = 30 000;
50 000 - 30 000 = 20 000); или в результате рассуждений: сумма (х + 20 000) — это число х да еще число 20 000; тогда число х — это сумма (х + 20 000)без числа 20 000; значит, число х меньше суммы (х + 20 000) на 20 000;
б) х = 12 800; делимое больше чем частное на 9600 (12 800 - 3200 = 9600).
Д) Задания 10, 11.
Задание 10.
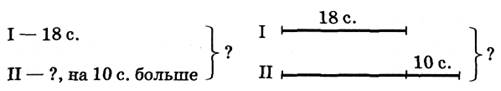
Ответ: повесть занимает 46 страниц.
7.Подведение итогов урока
8.Рефлексия
Урок 81
Тема урока. Смысл действия деления.
Цели урока:1)обобщить знания по раскрытию конкретного смысла действия деления на примере задач;
2) решать задачи на движение.
3) развивать навык устных и письменных вычислений;
4) снижать уровень тревожности на уроке;
5 )воспитывать интерес к урокам математики
Ход урока
1.Организационный момент
2. Проверка домашнего задания
3. Устный счёт
4.Работа по учебнику
(У) Задания1, 2, 6*.
Задание1.Ученики составляют выражения к задачам: а) а : 8; б) 36 : с; в) k • т. Можно дать значения буквам, сделать вычисления, составить и решить обратные задачи. В результате дети убеждаются во взаимосвязи умножения и деления: найти частное от деления числа а на число Ъ означает найти такое число с, что b • с - а.
Задание 2. По выражению 42 : 7 дети составляют простые задачи с разным содержанием. Но при этом нужно следить, чтобы прозвучали все виды простых задач: деление на равные части, деление по содержанию, уменьшение числа в несколько раз, кратное сравнение.
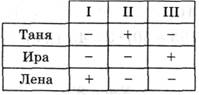Задание 6*. Нужно установить соответствие между тремя девочками (Таня, Ира, Лена) и тремя местами (I, II, III)с учетом условий:
1)место Иры нечетное;
2)Таня заняла не первое место;
3)место у Лены выше, чем у Иры.
Из 1) и 3) следует, что у Иры III место. Остались места I и ІІ.
Из 2) следует, что у Тани II место. Тогда I место у Лены.
5.Работа в тетрадях
(П) Задания3, 5, 4, 7, 8.
Задание5. Что означает «обратный путь"? Сколько это километров? На какой путь лодка затратила меньше времени? Почему? Почему скорость лодки по течению всегда больше, чем скорость против течения?
 |
Физкультминутка
Задание 8. Сначала нужно нарисовать прямоугольник с площадью 20 см2. Таких прямоугольников может быть три: с размерами 1 см и 20 см; 2 см и 10 см; 4 см и 5 см. Прямоугольник, площадь которого в 2 раза меньше, можно нарисовать, вычислив его размеры по площади 10 см2: 1 см и 10 см или 2 см и 5 см. А можно рассуждать так: чтобы произведение (площадь) уменьшить в 2 раза, нужно один из множителей (сторону) уменьшить в 2 раза. Теперь можно из трех первых прямоугольников образовать новые.
 |
Д) Задания 9,10
Задания 9(65 - 50) • 3 = 45 (км) – будет расстояние через 3 часа
7.Подведение итогов урока
8.Рефлексия
Урок 82