Теорема 6.9. Если в матрице системы (6.1) имеет место диагональное преобладание, то метод Зейделя (6.13) сходится, причем быстрее, чем метод Якоби (6.9а)

Замечание 6.4. В соответствии с последней теоремой в методе Зейделя (6.13) вместо оценок (6.17), требующих дополнительных затрат на обращение треугольной матрицы, допустимо использование оценок погрешности метода Якоби. Естественно, они заведомо грубее.

Остановимся еще на одном важном для приложений классе систем вида (6.1), для которых имеет место сходимость метода Зейделя(6.13).

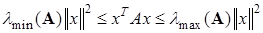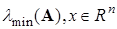
Определение (6.1). Система называется нормальной, если матрица – симметричная положительно определенная.( ) Матрица называется положительно определенной.если ее собственные числа больше 0. Эрмитово положительно определена,если ее собственные числа имебт положительные вещественные части. ,где -собственное число матрицы

Теорема 6.10. Если система (6.1) – нормальная, то метод Зейделя (6.13) сходится.