Решение плоской задачи теории упругости методом конечных элементов
13.1 Цель работы
Целью работы является изучение метода конечных элементов на примере решения плоской задачи теории упругости с использованием линейных треугольных элементов.
13.2 Задания
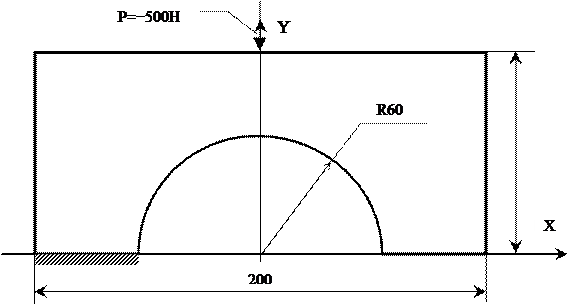
Толщина деталей принимается равной 1.
 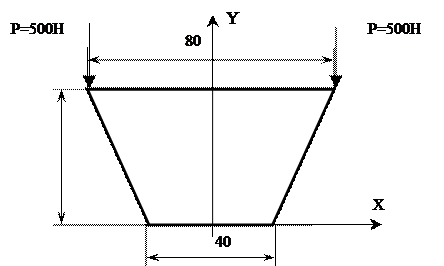 |
№ 1
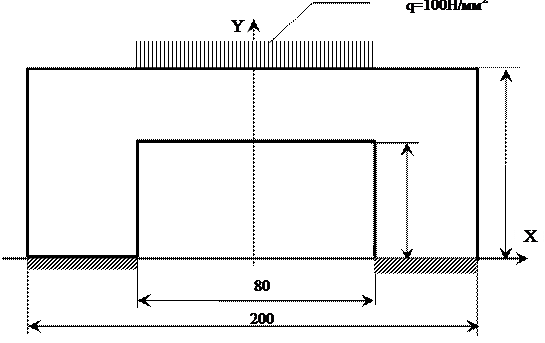 № 2
№ 2
 |


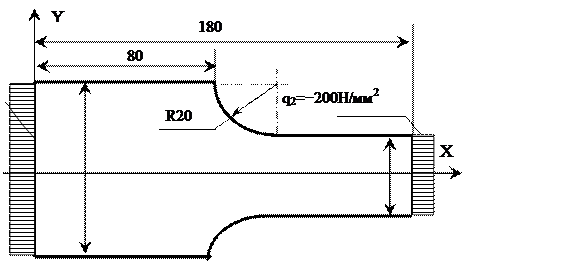 № 3
№ 3
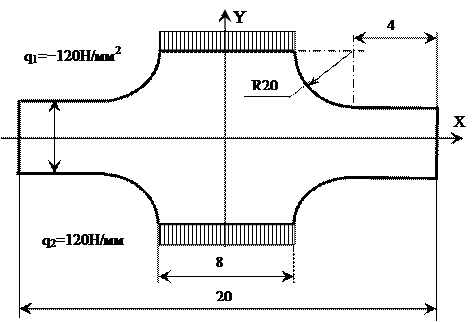 № 4
№ 4
  |
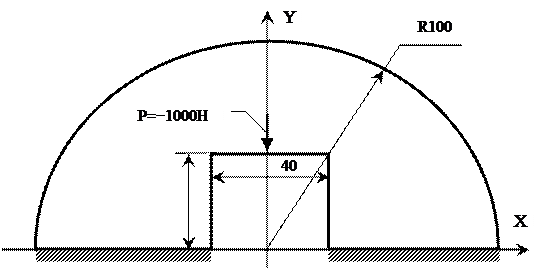
№ 5
 |


 № 6
№ 6


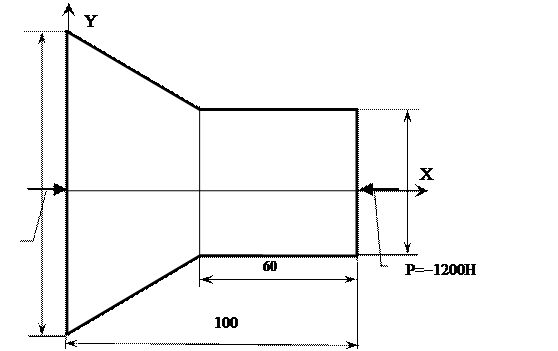
 № 7
№ 7


 № 8
№ 8
13.3 Краткие теоретические сведения
В плоской задаче теории упругости рассматривают два случая – плоское деформированное состояние и плоское напряженное состояние.
Для плоского напряженного состояния компоненты тензора напряжений sz=tzx=tzy=0, компоненты тензора деформаций gyz= gxz=0, а ez величина постоянная. Для плоского деформированного состояния компоненты тензора деформаций ez=gxz=gyz=0, компоненты тензора напряжений tzy=tzx=0, а sz величина постоянная. Конечноэлементное решение для обоих случаев строится одинаково, но с разными матрицами упругих постоянных.
Схема нагружения упругого тела показана на рисунке 13.1.
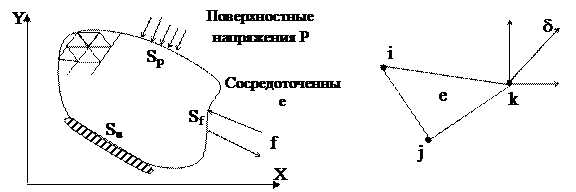 |
 |
 |
На части границы Sp действуют поверхностные напряжения (распределенная нагрузка), на части границы Sf приложены сосредоточенные силы, а на части границы Su заданы условия закрепления или известные перемещения. Перемещение каждой точки тела определяется вектором d с горизонтальной компонентой w и вертикальной компонентой V. Напряженно-деформированное состояние упругого тела характеризуется вектором деформаций {e} и вектором напряжений {s} c компонентами

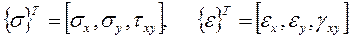 ,
,
где sx,sy – нормальные напряжения по оси X и по оси Y, txy – касательное напряжение; ex,ey – нормальные деформации по оси X и по оси Y, gxy – деформация сдвига.
Между деформациями и перемещениями в двумерном случае имеют место соотношения
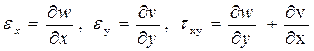 . (13.1)
. (13.1)
Компоненты напряжений связаны с компонентами деформации законом Гука 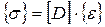 , где [D] – матрица упругих констант. В случае плоского напряженного состояния матрица [D] имеет вид
, где [D] – матрица упругих констант. В случае плоского напряженного состояния матрица [D] имеет вид
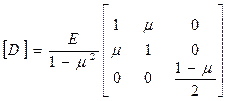 , (13.2)
, (13.2)
где E – модуль упругости, m - коэффициент Пуассона.
Предполагается, что материал изотропен.
В случае плоской деформации матрица [D] имеет вид
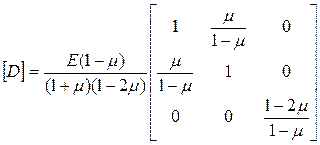 . (13.3)
. (13.3)
Уравнения равновесия без учета объемных сил имеют вид
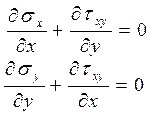 . (13.4)
. (13.4)
Решение уравнений (13.4) ищется для заданных граничных условий, в качестве которых задают на части границы Sp поверхностные силы, на части границы Sf сосредоточенные силы, а на другой части Su – перемещения (кинематические условия).
В методе конечных элементов неизвестная функция, являющаяся решением заданного дифференциального уравнения, аппроксимируется множеством полиномов, определенных на конечном числе подобластей, называемых конечными элементами.
Далее рассматриваются треугольные конечные элементы, простейшие для двумерных областей. Нумерация узлов и обозначения неизвестных показаны на рисунке 7.2.
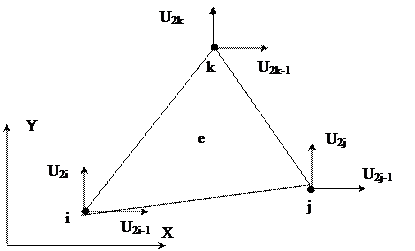 |
Рис.13.2
Нумерация перемещений узлов конечного треугольного элемента
I,J,K – номера узлов,
U2i-1,U2j-1,U2k-1 – горизонтальные перемещения,
U2i,U2j,U2k - вертикальные перемещения.
Перемещения внутри треугольного конечного элемента вычисляются c помощью интерполяционного полинома
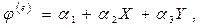 (13.5)
(13.5)
где e – номер элемента;j(e) - горизонтальное или вертикальное перемещение;a1,a2,a3 – коэффициенты полинома; X,Y – координаты точки внутри элемента.
Коэффициенты полинома определяются из условий Лагранжа
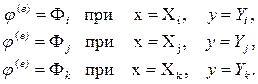
Подставив эти условия в (13.5) получим систему уравнений
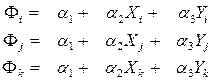 , (13.6)
, (13.6)
где i,j,k – номера узлов элемента; X,Y – координаты узлов элемента; Fi,Fj,Fk – перемещения узлов; a1,a2,a3 – коэффициенты полинома.
Решая систему (13.6) получим
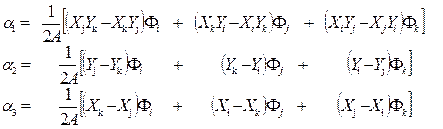
где A – площадь треугольника.
Введем обозначения
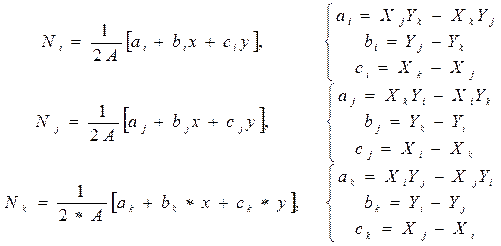 , (13.7)
, (13.7)
где Ni, Nj, Nk – функции формы элемента.
Тогда интерполяционный полином внутри элемента можно записать в виде j(e) = NiFi + NjFj + NkFj .
С учетом обозначений на рисунке 13.1 горизонтальные и вертикальные перемещения внутри элемента можно записать
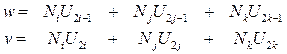
Запишем выражения для перемещений внутри элемента в расширенном виде
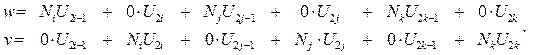 (13.8)
(13.8)
Или в матричной форме
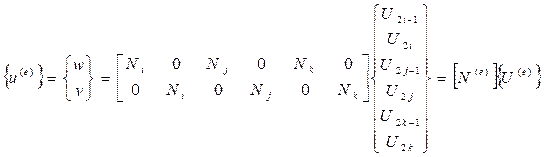 (13.9)
(13.9)
где [N(e)] – матрица функций формы элемента;
{U(e)} – вектор столбец перемещений узлов элемента;
{u(e)} – перемещения внутри элемента.
Перемещения для группы элементов определяются по формуле
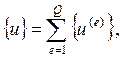 где Q – количество элементов.
где Q – количество элементов.
Вычислим первые производные функций перемещения внутри элемента (градиенты), необходимые для вычисления деформаций (13.1), используя соотношения (13.8)
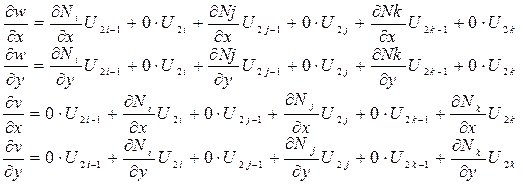
Из формул (13.7) следует, что 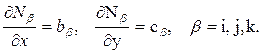
Поэтому
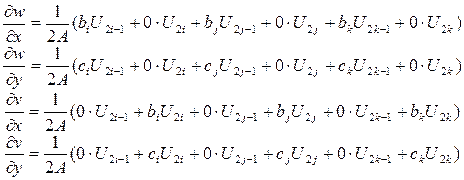 . (13.10)
. (13.10)
Подставим выражения для производных (13.10) в выражения для деформаций (13.1). После преобразований получим
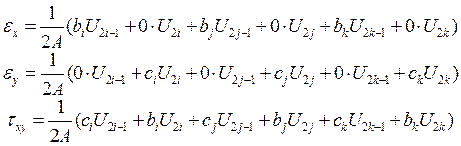 .
.
В матричной форме последнее выражение можно записать в виде
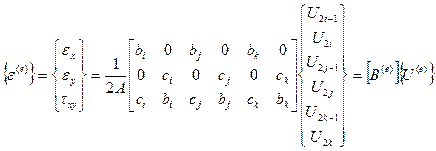 (13.11),
(13.11),
Где 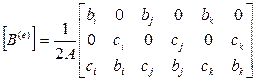
матрица градиентов конечного треугольного элемента.
Подставляя (13.10) в выражение для закона Гука получим
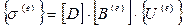 (13.12).
(13.12).
Значения элементов матрицы градиентов [B(e)] внутри треугольного элемента постоянны, а следовательно будут постоянными компоненты вектора деформаций {e(e)} и вектора напряжений {s(e)}.
Запишем систему уравнений равновесия (13.4) относительно перемещений. Для этого, подставим в (13.4) соотношения между напряжениями и перемещениями. Например, используя закон Гука и выражения (13.1), для случая плоского напряженного состояния получим
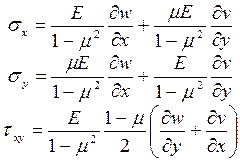 (13.13).
(13.13).
Подставив (13.12) в (13.4) получим
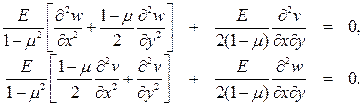 (13.14)
(13.14)
Решением системы уравнений (13.14) будут функции горизонтальных и вертикальных перемещений, удовлетворяющих заданным граничным условиям.
Теорема. Из всех перемещений, удовлетворяющих кинематическим граничным условиям, стационарное (экстремальное) значение потенциальной энергии сообщают те перемещения, которые удовлетворяют уравнениям равновесия.
Полная потенциальная энергия упругой системы состоит из энергии деформации в теле и потенциальной энергии приложенных поверхностных сил, которая противоположна по знаку работе внешних сил. В соответствии с этим полную потенциальную энергию c запишем в виде c = L - Y, (13.15)
где L - энергия деформаций, Y – работа внешних сил.
Для разбитой на элементы области равенство (7.15) записывается в виде суммы по элементам 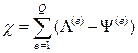 (13.16).
(13.16).
Энергия деформаций отдельного элемента вычисляется по формуле
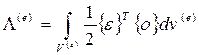 (13.17),
(13.17),
где v(e) – объем элемента. Подставив в (13.17) выражения (13.10) и (13.11), после преобразований получим
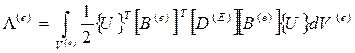 (13.18).
(13.18).
Работа, совершаемая внешними силами, состоит из работы сосредоточенных в узлах сил Yf и работы распределенной на внешней поверхности нагрузки (давлений) Yp.
Работа сосредоточенных сил вычисляется как произведение
Yf = {u}T{P} (13.19),
где {u} – вектор перемещений узлов, {P} - вектор заданных сосредоточенных сил. Предполагается, что в узле силы разложены на горизонтальную Px и вертикальную Py компоненты, т.е.
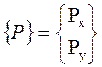 .
.
Работа Yp вычисляется на части границы Sq, на которой задана распределенная нагрузка.
Для разбитой на элементы области граница Sq будет состоять из сторон конечных элементов.
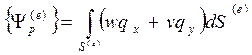 ,
,
где qx,qy – соответственно горизонтальная и вертикальная составляющие распределенной нагрузки, S(e) – площадь нагруженной стороны элемента. C учетом (13.9), выражение для Yp(e) можно записать в виде
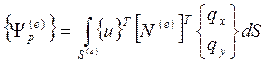 (13.20).
(13.20). 

Подставив выражения (13.18), (13.19), (13.20) в (13.16) получим выражение для полной потенциальной энергии

(13.21).
Потенциальная энергия будет иметь минимальное значение при условии равенства нулю ее производной по {u}
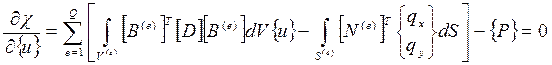
(13.22).
Введем обозначения
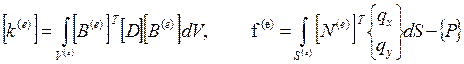 (13.23),
(13.23),
где [k(e)] – матрица жесткости элемента, [f(e)] – вектор нагрузки элемента.
С учетом введенных обозначений, выражение (13.22) запишется в виде
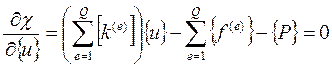
или
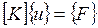 (13.24),
(13.24),
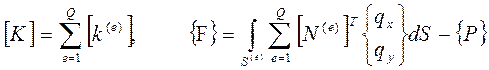
где [K] – глобальная матрица жесткости, {F} – глобальный вектор нагрузки.
Выражение (13.24) представляет собой систему линейных алгебраических уравнений, решением которой является искомый вектор перемещений {u}.
Матрицы [B(e)] и [D] содержат константы, что позволяет вычислить объемный интеграл в выражение (7.23) для матрицы жесткости линейного треугольного элемента
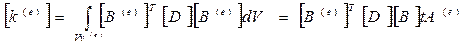 ,
,
где t – толщина элемента, A(e) – площадь элемента.
Построение сетки треугольных элементов
При решении задач механики сплошных сред методом конечных элементов двумерная область, в которой ищется решение заменяется дискретной моделью. Эта модель строится из многоугольников (треугольников или четырехугольников), называемых конечными элементами и объединенных в узлах.
Сетка конечных элементов считается заданной, если определены номера элементов и узлов, и их координаты. Данные о сетке элементов требуют подготовки большого объема информации. Неверно заданная информация об элементах является одним из основных источников ошибок при решении задач методом конечных элементов. Устранить эти ошибки возможно, если автоматизировать подготовку исходных данных о сетке элементов с помощью специальной программы.
Область, в которой ищется решение предварительно разбивается на несколько фрагментов. Начало координат выбирается произвольно. Выбранная система координат называется глобальной. В каждом фрагменте в вершинах и на сторонах проставляются узловые точки. На плоскости X,Y задаются координаты узловых точек.
Каждый фрагмент отображается на квадрат с локальными координатами x,h. Начало координат x,h выбирается в центре квадрата. Координаты x и h изменяются от -1 до 1. Такая система координат называется естественной.
В локальной системе координат фрагмент разбивается на прямоугольники. Полученные в локальной системе координат новые узловые точки отображаются обратно в глобальную систему координат по формулам
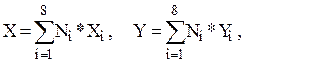 (13.25)
(13.25)
где Xi, Yi - глобальные координаты узлов фрагмента; Ni(x,h) - функции формы; X,Y - координаты новых узлов фрагмента, полученные после разбиения; 8 - начальное количество узлов фрагмента.
В качестве фрагментов используют четырехугольные элементы с восемью узлами. Функции Ni представляют собой полиномы второго порядка относительно локальных координат x и h. Поэтому отображение (13.25) будет квадратичным, а стороны элементов - параболы. Квадратичное отображение позволяет строить дискретную модель области с криволинейными границами.
Функции формы в выражении (13.25) для квадратичного отображения имеют вид
| N1=-0.25(1-x)(1-h)(x+h+1); N3= 0.25(1+x)(1-h)(x-h-1); N5= 0.25(1+x)(1+h)(x+h-1); N7=-0.25(1-x)(1+h)(x-h+1); | N2 = 0.5(1-x2)(1-h); N4 = 0.5(1-h2)(1+x); (13.26) N6 = 0.5(1-x2)(1+h); N8 = 0.5(1-h2)(1-x). |
Построение сетки с помощью квадратичного отображения для одного фрагмента показано на Рис.13.3.
                а а
   | ||||||||||||||||||||||||||||||
 
      
|
Рис 13.3
Квадратичное отображение
На этом же рисунке показаны глобальные X,Y и локальные x,,h координаты. Номера узлов в локальной системе координат изменяются от 1 до 8. Узлу 1 всегда соответствуют координаты x=h=-1. Остальные узлы нумеруются против часовой стрелки. В глобальной системе координат узлы нумеруются произвольно.
Равномерность разбиения фрагмента на элементы зависит от начального положения узлов 2,4,6,8 расположенных на стороне фрагмента. При сдвиге этих узлов от середины стороны сетка элементов будет неравномерной. Положение узлов на стороне фрагмента в локальной системе координат должно удовлетворять неравенствам
-1/2 < x < 1/2, -1/2 < h < 1/2. (13.27)
Дискретная модель области обычно конструируется из нескольких четырехугольных фрагментов, имеющих общие стороны. При переходе к новому фрагменту необходимо проверять каждую сторону на связность с другими фрагментами. Информация о соединении фрагментов задается матрицей связности. Количество строк в матрице равно числу фрагментов. Количество столбцов равно 4 (число сторон фрагмента). Если сторона не связана, то в строке матрицы связности, соответствующей номеру фрагмента и в колонке, соответствующей номеру стороны записывается 0. В противном случае записывается номер фрагмента, с которым граничит сторона. Порядок нумерации сторон фрагмента в локальной системе координат показан на Рис. 13.3б. Узлы на общей стороне фрагментов должны иметь одинаковые номера. Таким образом, для построения сетки элементов необходимо выполнить следующие действия:
1. Заданную область предварительно разбить на четырехугольные фрагменты с восемью узлами. Каждому фрагменту и узлу присваивается номер. Нумерация узлов и фрагментов выполняется произвольно. Выбирается глобальная система координат, в которой задаются X и Y координаты узлов.
2. В каждом фрагменте выбирается локальная система координат. Задается матрица связности фрагментов. Стороны фрагмента нумеруются в соответствии с Рис. 13.3б.
3. В каждом фрагменте задается количество разбиений по координатам x и h. Количество разбиений по x называется числом строк, а по h - числом столбцов. Для каждого фрагмента указываются глобальные номера узлов, заданные в пункте 1.
4. Фрагмент отображается на квадрат в локальной системе координат. В соответствии с заданным количеством строк и столбцов фрагмент разбивается на новые четырехугольники. По формулам (13.25) вычисляются координаты новых узлов в глобальной системе (обратное отображение). Полученные после разбиения узлы последовательно нумеруются, начиная от точки с координатами x = -1, h = +1 и двигаясь слева направо (при изменении x от -1 до +1) и сверху вниз (при изменении h от +1 до -1).
5. Номера граничных узлов сохраняются и используются при рассмотрении соседних фрагментов. Все узлы, пронумерованные ранее, пропускаются.
13.4 Порядок выполнения работы
Все расчеты в работе выполняются с помощью программы ProFEM, работающей под управлением Windows 98 и выше. Этапы расчетов и описание элементов интерфейса программы ProFEM даны ниже.
1. Перед выполнением лабораторной работы студент должен ознакомиться с методическими указаниями.
2. Получить у преподавателя задание.
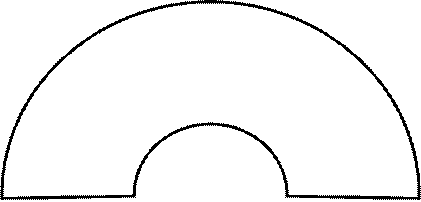
Пример рассчитываемой детали представлен на рисунке 13.4. Деталь нагружена сосредоточенной силой по оси симметрии. Поэтому сетку элементов можно строить для половины детали.
 

  

 

|
Рис. 13.4
Разбиение детали на фрагменты
3.Деталь предварительно разбивается на фрагменты, которые последовательно нумеруются k=1..Mf, где Mf – номер последнего фрагмента.
4. В каждом фрагменте задается восемь узлов (четыре узла в углах фрагмента и четыре - на сторонах). Каждому узлу присваивается номер j=1..Mn, где Mn – номер последнего узла.
5. Задаются X и Y координаты узлов фрагментов. В каждом фрагменте задается локальная система координат xk,hk. Номера j=1..Mn и координаты узлов записываются в таблицу 13.1.
Таблица координат узлов фрагментов (Mf=2, Mn=13)
Таблица 13.1
| Номер узла j | Координаты узлов | Номер узла j | Координаты узлов | ||
| Xj координата | Yj координата | Xj координата | Yj координата | ||
| 4.2 | 4.2 | ||||
| 1.86 | 0.78 | ||||
| 5.5 | 2.25 | ||||
| 0.78 | 1.84 | ||||
| 2.36 | 5.47 | ||||
| 1.41 | 1.4 | ||||
| 2.77 | 2.76 |
6. Составляется матрица связности фрагментов.
Таблица соединения фрагментов Таблица 13.2
| Номер фрагмента | Стороны фрагментов | |||
7. В каждом фрагменте задается количество разбиений (число строк и столбцов) и номера узлов фрагмента. Количество разбиений фрагмента зависит от требуемой точности вычислений напряженно-деформированного состояния и окончательно определяется после серии расчетов.
Таблица данных о разбиении фрагментов и
связи глобальных и локальных номеров узлов Таблица 13.3
| Номер фрагмента. | x строки | h столбцы | ||||||||
8. Запустить программу ProFEM - откроется окно меню (Рис. 13.5).

Рис.13.5.
Главное меню программы ProFEM
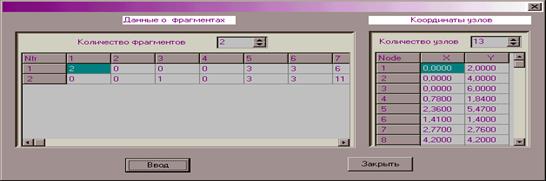 |
В меню « Файл » выбрать команду «Новый», после чего откроется диалоговое окно ввода данных о фрагментах (Рис. 13.6).
Рис. 13.6.
Диалоговое окно ввода данных о фрагментах
В начале вводят количество фрагментов и количество узлов. В колонках 1-4 левого поля Рис.13.6 вводят значения матрицы соединений таблицы 13.2, в колонках 5,6 количество разбиений и в колонках 7-14 глобальные номера узлов из таблиц 13.3. В правом поле Рис.13.6 вводят координаты узлов из таблицы 13.1. Для продолжения расчетов необходимо нажать кнопку «Ввод».
Введенные данные могут быть сохранены в файле. Для этого надо в меню «Файл» выбрать команду «Сохранить» или «Сохранить как».
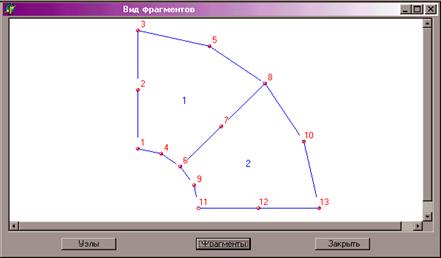 |
9. В меню «Фрагменты» выбрать команду «Вид», в результате откроется окно с графическим изображением рассчитываемой области, разбитой на фрагменты (Рис.13.7).
Рис. 13.7.
Диалоговое окно просмотра фрагментов
Если будут обнаружены ошибки, то в меню «Фрагменты» надо выбрать команду «Редактировать». В открывшемся окне «Данные о фрагментах» (Рис.13.6) исправить ошибки. После устранения ошибок перейти к следующему этапу.
10. В меню «Сетка» выбрать команду «Построить». Результаты построения сетки могут быть представлены в виде таблицы с помощью команды «Таблица» или в графическом виде с помощью команды «Вид» меню «Сетка». Графическое представление построенной сетки показано на рисунке 13.8.
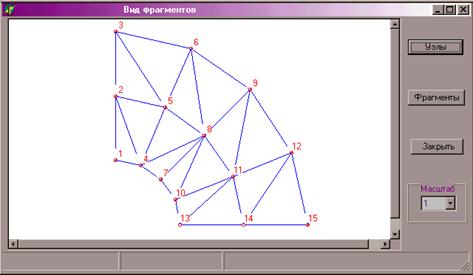 |
Рис. 13.8.
Диалоговое окно просмотра сетки элементов
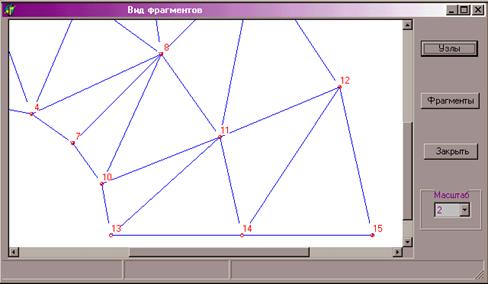 |
Кнопки «Узлы» и «Элементы» выводят или стирают соответствующие номера. В списке «Масштаб» можно выбрать масштабный коэффициент отображения сетки, который по умолчанию равен единице. Пример отображения сетки с масштабным коэффициентом 2 показан на рисунке 13.9.
Рис. 13.9.
Сетка элементов в увеличенном масштабе
Для построения другого варианта сетки, необходимо выбрать в меню «Фрагменты» команду «Редактировать», внести изменения в данные о фрагментах и повторить построение сетки. Результаты построения сетки могут быть представлены в табличной форме. Для этого в главном меню необходимо выбрать «Сетка», «Таблица».
11. После построения сетки можно перейти к расчету напряженно-деформированного состояния области (детали) при заданных граничных условиях (нагрузки и условий закрепления). По умолчанию установлено решение задачи о плоском напряженном состояние. Выбор плоского деформированного состояния выполняется соответствующей кнопкой. В строках ввода «Модуль упругости» и «Коэффициент Пуассона» задать необходимые значения и нажать кнопку «Ввести». После нажатия кнопки «Сборка» вычисляются матрицы жесткости элементов и глобальная матрица системы уравнений. Далее вводятся граничные условия, в качестве которых задают горизонтальные и вертикальные силы, и горизонтальные и вертикальные перемещения. В колонке 1 вводят номер узла, в колонке 2 – значение силы или перемещения. После нажатия кнопки «Решение» решается система уравнений, и определяются перемещения в узлах сетки.
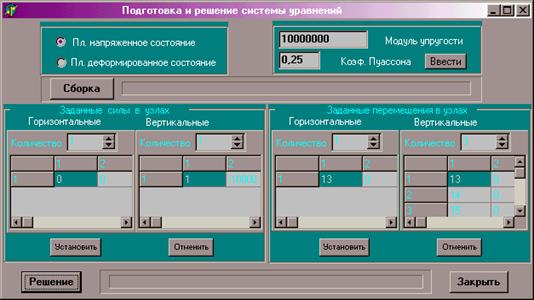 |
Рис.13.10
Диалоговое окно ввода свойств материала,
граничных условий и решения системы уравнений
12 Для просмотра результатов в главном меню программы ProFEM необходимо выбрать «Задача», «Результаты», что приведет к открытию диалогового окна, показанного на рисунке 13.11. В левом поле необходимо выбрать выводимый параметр
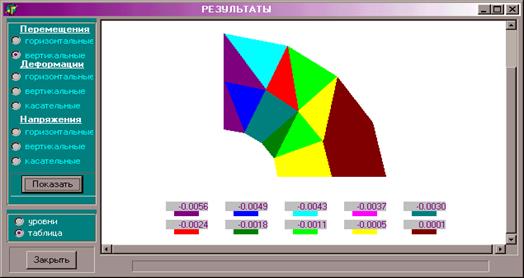 |
Рис.13.11
Диалоговое окно результатов
 |
Результаты могут быть представлены в графическом (кнопка
«Уровни») и табличном (кнопка «Таблица») виде.
Рис.13.12
Окно просмотра таблиц результатов
В левой таблице выводятся перемещения в узлах сетки. В правой таблице выводятся значения перемещений, деформаций и напряжений в элементах.
13.5 Содержание отчета
Отчет по лабораторной работе должен содержать:
- Цель лабораторной работы с указанием заданной области, для которой необходимо построить сетку элементов.
- Изображение области с начальным разбиением на фрагменты.
- Исходные данные для программы, которые должны включать координаты узлов в глобальной системе, матрицу связности фрагментов, количество разбиений и номера узлов фрагментов.
- Графическое изображение сетки элементов, построенное по результатам расчета по программе.
13.6 Контрольные вопросы.
1. Что используется в качестве фрагментов области, которая разбивается на элементы?
2. Какая система координат называется естественной?
3. Как задается глобальная система координат?
4. Как нумеруются узлы и стороны фрагмента?
5. Как выполняется отображение фрагмента из локальной системы координат в глобальную?
6. Какое отображение называется квадратичным?
7. Что называется функциями формы?
8. Как задается матрица связности фрагментов?
9. Как задается количество разбиений фрагментов?
10.Какие граничные условия необходимо задать в плоской задаче теории упругости?
11.Какой порядок интерполяционного полинома имеют линейные треугольные элементы?
12.Какие характеристики материала необходимо задать в задаче теории упругости?
13.Какими компонентами характеризуется напряженно-деформированное состояние тела в плоской задаче теории упругости?
14.Как аппроксимируется искомое решение в методе конечных элементов?
13.7 Литература.
1.Сегерлинд Л. Применение метода конечных элементов.- М., Мир, 1979.
2.Зенкевич О., Морган К. Конечные элементы и аппроксимация.- М.,Мир,1986.
3.Морозов Е.М., Никишков Г. П. Метод конечных элементов в
механике разрушения. - М., Наука, 1980.
4.Фадеев А.Б. Метод конечных элементов в геомеханике. М.: Недра, 1987.
