Действия над комплексными числами
Равенство двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 означает равенство их действительных и мнимых частей: 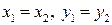 .
.
Сложение, вычитание, умножение и деление комплексных чисел в алге-браической форме определяются следующим образом. Если z1 = x1 + iy1, z2 = x2 + iy2, то
1) z1 + z2 = (x1 + x2) + i(y1 + y2);
2) z1 – z2 = (x1 – x2) + i(y1 – y2);
3) z1 z2 = (x1x2 – y1y2) + i(x1y2 + х2y1);
4) 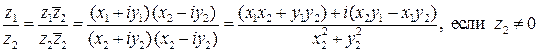 .
.
Пример. Даны числа z1 = 4 – i и z2 = 1 + 3i. Вычислить 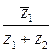 .
.
Найдем 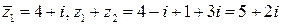 , затем выполняем деление при помощи домножения числителя и знаменателя на число, сопряженное знаменателю:
, затем выполняем деление при помощи домножения числителя и знаменателя на число, сопряженное знаменателю:
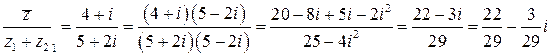
(при вычислениях учтено, что 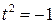 ).
).
Умножение, деление, возведение в натуральную степень и извлечение корня из комплексных чисел в тригонометрической форме определяются следующим образом:
если 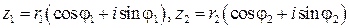 , то
, то
1) 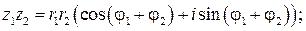
2) 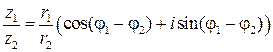 , если r2 ¹ 0;
, если r2 ¹ 0;
если 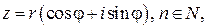 то
то
3) 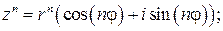 (15)
(15)
4) 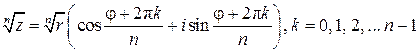 .
.
В ответ записываются главные значения аргумента полученного
результата, заключенные в промежутке 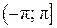 .
.
Примерный вариант и образец выполнения контрольной работы 3
Задача 1. Даны функции 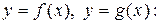
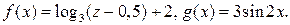
Требуется:
1) используя графики основных элементарных функций, построить графики функций f (x) и g (x). Описать при помощи построенных графиков основные характеристики этих функций: ООФ, ОЗФ, четность, периодичность, промежутки монотонности и экстремумы;
2) составить сложные функции y = f ( g ( x )) и y = g ( f ( x ));
3) для функции y = f ( x ) найти обратную функцию y = f –1( x ),
построить графики обеих взаимно обратных функций в одной системе
координат и записать их ООФ и ОЗФ.
Задача 2. Вычислить пределы, применяя правила раскрытия неопределенностей, основные теоремы о конечных пределах, теоремы обесконечно малых и бесконечно больших функциях. Ответы пояснить с точки зрения определения предела.
а) 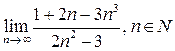 ; б)
; б) 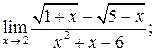
в) 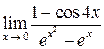 ; г)
; г) 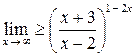 .
.
Задача 3. Исследовать непрерывность функций в соответствии с зада-ниями.
а) Проверить, является ли функция 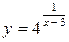 непрерывной в точках х1 = 0 и х2 = 3. В случае разрыва функции указать тип разрыва и сделать схематический чертеж в окрестности точки разрыва.
непрерывной в точках х1 = 0 и х2 = 3. В случае разрыва функции указать тип разрыва и сделать схематический чертеж в окрестности точки разрыва.
б) Построить график функции 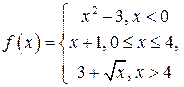 используя график, записать промежутки непрерывности функции, перечислить точки разрыва и указать тип каждого из них.
используя график, записать промежутки непрерывности функции, перечислить точки разрыва и указать тип каждого из них.
Задача 4. Даны уравнение 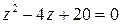 , комплексное число
, комплексное число 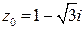 и натуральное число n = 6. Требуется:
и натуральное число n = 6. Требуется:
1) найти корни уравнения z1, z2 на множестве комплексных чисел;
2) найти комплексное число 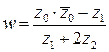 в алгебраической форме;
в алгебраической форме;
3) получить тригонометрическую форму числа z0 и вычислить с ее помощью 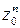 . Ответ записать в тригонометрической и в алгебраической формах.
. Ответ записать в тригонометрической и в алгебраической формах.
 Решение задачи 1
Решение задачи 1
1) Строим графики заданных функций,
используя известные графики основных элементарных функций и простейшие преобразования графиков.
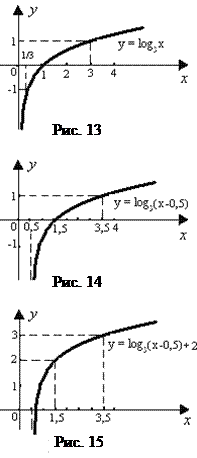
Для построения графика 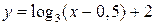 в качестве исходного используем график функции y = log3 x, для которой ООФ: х > 0, у(1) = 0, у(3) = 1, y(1/3) = –1 (рис. 13).
в качестве исходного используем график функции y = log3 x, для которой ООФ: х > 0, у(1) = 0, у(3) = 1, y(1/3) = –1 (рис. 13).
График функции 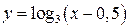 получаем из исходного графика
получаем из исходного графика 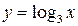 в соответствии
в соответствии
с преобразованием графиков
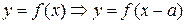
(перенос графика на а единиц в направлении
оси Ох). В данном случае график перемещаем
на 0,5 единиц вправо (рис. 14).
Для функции 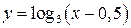 ООФ: х > 0,5, у(1,5) = 0, у(3,5) = 1.
ООФ: х > 0,5, у(1,5) = 0, у(3,5) = 1.
График 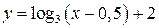 получаем из графика
получаем из графика 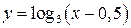
в соответствии с преобразованием графиков 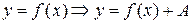
(перенос графика на А единиц в направлении оси Oу). В данном случае график перемещаем на 2 единицы вверх (рис. 15).
Для построения графика 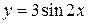 в качестве исходного используем график функции
в качестве исходного используем график функции 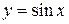 (рис. 16).
(рис. 16).
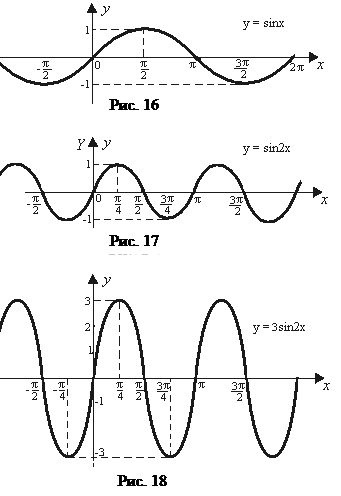 График функции
График функции 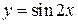 получаем из исходного графика в соответствии с преобразованием графиков
получаем из исходного графика в соответствии с преобразованием графиков 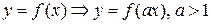 (сжатие графика в а раз в направлении оси Ох). В данном случае график сжимаем в 2 раза (рис. 17).
(сжатие графика в а раз в направлении оси Ох). В данном случае график сжимаем в 2 раза (рис. 17).
График функции 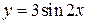 получаем из графика функции
получаем из графика функции 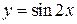 в соответствии с преобразованием графиков
в соответствии с преобразованием графиков 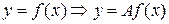 ,
, 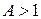 (растяжение графика
(растяжение графика
в А раз в направлении оси Оу). В данном случае график растягиваем в 3 раза (рис. 18).
Опишем при помощи пост-роенных графиков основные характеристики функций 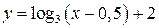
и 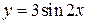 в виде таблицы.
в виде таблицы.
Таблица 2
| № | Характеристика | 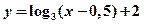 | 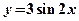 |
| ООФ (область определения функции) | 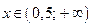 | 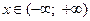 | |
| ОЗФ (область значений функции) | 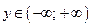 | 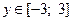 |
Окончание табл. 2
| № | Характеристика | 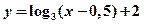 | 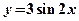 |
| Нули функции | 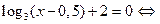 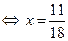 | 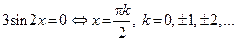 | |
| Четность | Общего вида | Нечетная | |
| Периодичность | Непериодическая | Периодическая с 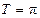 | |
| Промежутки монотонности | 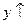 при при 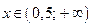 | 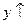 при при 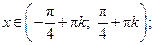 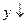 при при 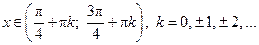 | |
| Точки экстремумов, экстремумы функции | Экстремумов нет | 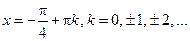 – точки min, – точки min, 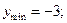 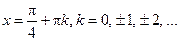 – точки max, – точки max, 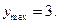 |
2) Составим сложную функцию 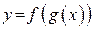 для
для 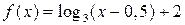 ,
, 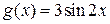 , подставив в f (x) вместо аргумента х функцию g(x):
, подставив в f (x) вместо аргумента х функцию g(x): 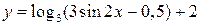 .
.
Аналогично составляем сложную функцию 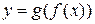 :
: 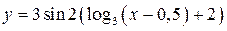 , т. е.
, т. е. 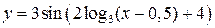 .
.
3) Находим обратную функцию для функции 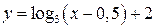 .
.
Так как функция является монотонно возрастающей на всей своей ООФ
(рис. 15), то для нее существует обратная функция 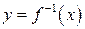 . Чтобы записать ее аналитическое выражение, решим уравнение
. Чтобы записать ее аналитическое выражение, решим уравнение 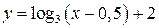 относительно х, т. е. получим выражение
относительно х, т. е. получим выражение 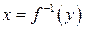 :
:
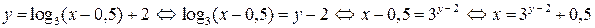 .
.
Переобозначив аргумент обратной функции через х, а функцию через у, получим: 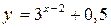 – функцию
– функцию 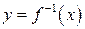 .
.
Для функции 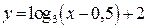 ООФ:
ООФ: 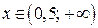 , ОЗФ:
, ОЗФ: 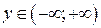 (табл. 2); для функции
(табл. 2); для функции 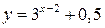 ООФ:
ООФ: 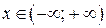 , ОЗФ:
, ОЗФ: 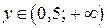 (для взаимно обратных функций промежутки ООФ и ОЗФ меняются ролями).
(для взаимно обратных функций промежутки ООФ и ОЗФ меняются ролями).
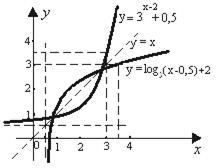 Построим графики обеих взаимно обратных функций
Построим графики обеих взаимно обратных функций 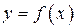 и
и 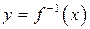 , контролируя их симметрию относительно биссектрисы первого и третьего координатных углов (рис. 19).
, контролируя их симметрию относительно биссектрисы первого и третьего координатных углов (рис. 19).
Ответы:
1) рис. 15, 18, табл. 2; Рис. 19
2) 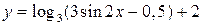 и
и 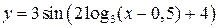 ;
;
3) 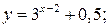 для
для 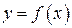 ООФ:
ООФ: 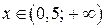 ОЗФ:
ОЗФ: 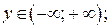 для
для 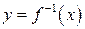 ООФ:
ООФ: 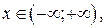 ОЗФ:
ОЗФ: 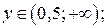 графики на рис. 19.
графики на рис. 19.
Решение задачи 2а
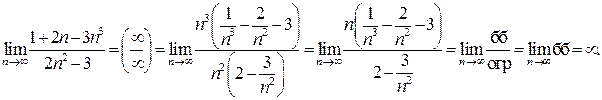
Для раскрытия неопределенности 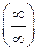 при n ® ¥ использовано правило 1: в числителе и знаменателе вынесены за скобки старшие степени n. При вычислении предела учтено, что при
при n ® ¥ использовано правило 1: в числителе и знаменателе вынесены за скобки старшие степени n. При вычислении предела учтено, что при 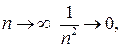 что
что 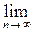 const = const, использованы теоремы о конечных пределах и теорема обесконечно больших функциях:
const = const, использованы теоремы о конечных пределах и теорема обесконечно больших функциях:
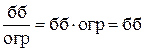 , если
, если 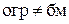 .
.
С точки зрения определения бесконечного предела последовательности 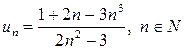 полученный результат
полученный результат 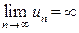 означает, что для достаточно больших значений номера n члены последовательности un
означает, что для достаточно больших значений номера n члены последовательности un
становятся сколь угодно большими по модулю.
Решение задачи 2б
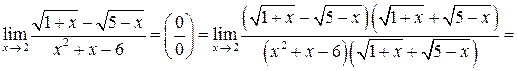
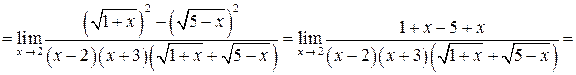
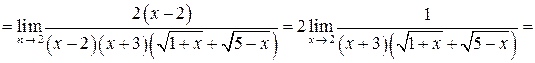
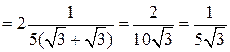 .
.
Здесь для раскрытия неопределенности 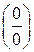 использовано правило 2: в числителе и знаменателе выделен критический множитель (х – 2).
использовано правило 2: в числителе и знаменателе выделен критический множитель (х – 2).
Для его выделения в знаменателе использовано разложение многочлена
на множители, а в числителе – домножение числителя и знаменателя
на выражение 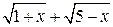 , сопряженное числителю
, сопряженное числителю 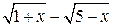 .
.
При вычислении предела использованы теоремы о конечных пределах.
С точки зрения определения предела функции 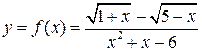 при
при 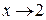 полученный результат
полученный результат 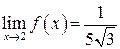 означает, что для значений аргумента х, достаточно близких к точке х = 2, значения функции будут становиться сколь угодно близкими к числу
означает, что для значений аргумента х, достаточно близких к точке х = 2, значения функции будут становиться сколь угодно близкими к числу 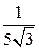 .
.
Решение задачи 2в
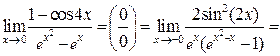
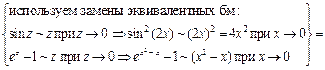
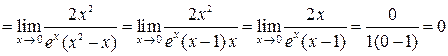 .
.
Для раскрытия неопределенности 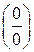 использовано правило 2:
использовано правило 2:
в числителе и знаменателе выделен критический множитель(х – 0) = х. Для его выделения использован принцип замены эквивалентных бесконечно малых.
С точки зрения определения конечного предела функции 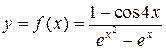 при
при 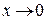 полученный результат
полученный результат 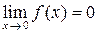 означает, что для значений аргумента х, достаточно близких к точке х = 0, значения функции будут становиться сколь угодно сколь угодно близкими к числу 0.
означает, что для значений аргумента х, достаточно близких к точке х = 0, значения функции будут становиться сколь угодно сколь угодно близкими к числу 0.
Решение задачи 2г
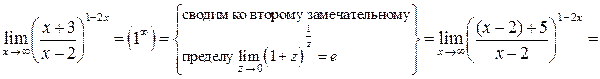
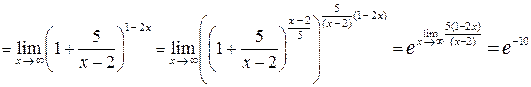 .
.
При вычислении предела использовано дважды правило раскрытия неопределенности 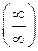 , образованной делением целых многочленов одинаковой степени (см. формулу (8)):
, образованной делением целых многочленов одинаковой степени (см. формулу (8)):
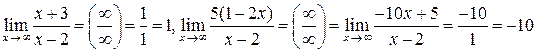 ,
,
а также непрерывность функции ez: 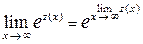 .
.
С точки зрения определения конечного предела функции 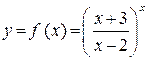 при
при 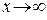 полученный результат
полученный результат 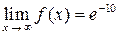 означает, что для достаточно больших (по модулю) значений аргумента х значения функции будут сколь угодно близкими к числу e–10.
означает, что для достаточно больших (по модулю) значений аргумента х значения функции будут сколь угодно близкими к числу e–10.
Ответы: а) 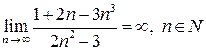 ; б)
; б) 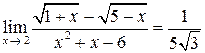 ;
;
в) 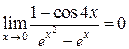 ; г)
; г) 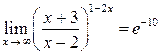 .
.
Решение задачи 3а
Чтобы проверить непрерывность заданной функции 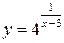 в каждой из заданных точек х1 = 0 и х2 = 3, используем определение непрерывности функции в точке.
в каждой из заданных точек х1 = 0 и х2 = 3, используем определение непрерывности функции в точке.
Найдем ООФ: 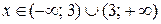 . Проверим выполнение условия (9) поочередно в точках х1 и х2.
. Проверим выполнение условия (9) поочередно в точках х1 и х2.
Точка х1 = 0:
1) х1 = 0 Î ООФ 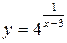 , причем окрестность точки х1 также входит
, причем окрестность точки х1 также входит
в ООФ;
2) существует конечный предел 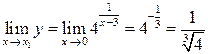 ;
;
3) справедливо 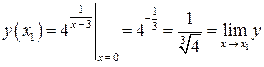 ;
;
следовательно, в точке х1 = 0 заданная функция непрерывна.
Точка х2 = 3:
1) х2 = 3 Ï ООФ 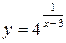 , следовательно, в точке х2 = 3 заданная функция не является непрерывной. Поскольку функция определена в окрестности точки х2, то эта точка является точкой разрыва функции.
, следовательно, в точке х2 = 3 заданная функция не является непрерывной. Поскольку функция определена в окрестности точки х2, то эта точка является точкой разрыва функции.
Чтобы определить тип разрыва, вычислим односторонние пределы функции при 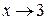 :
:
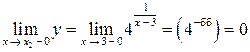 ;
; 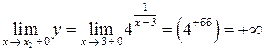
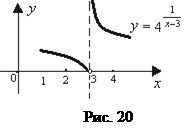 (при вычислении использовано предельное поведение показательной функции
(при вычислении использовано предельное поведение показательной функции 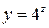 при
при 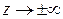 ). Так как один из односторонних пределов оказался бесконечным, делаем вывод, что разрыв
). Так как один из односторонних пределов оказался бесконечным, делаем вывод, что разрыв
в точке х2 = 3 бесконечный (разрыв 2-го рода).
Построим схематический чертеж графика функции в окрестности точки разрыва с учетом значений односторонних пределов (рис. 20).
Решение задачи 3б
Запишем ООФ кусочно-заданной функции.
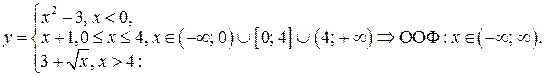
Построим график функции 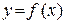 , объединяя "куски" графиков
, объединяя "куски" графиков
основных элементарных функций 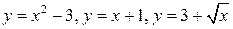 (рис. 21–24).
(рис. 21–24).
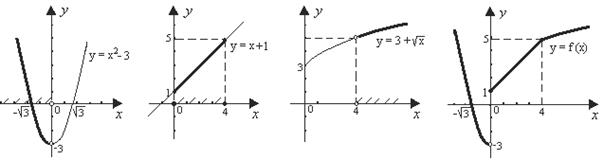
Рис. 21 Рис. 22 Рис. 23 Рис. 24
Анализируя график 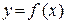 (рис. 24), видим, что он представляет
(рис. 24), видим, что он представляет
собой непрерывную линию для всех х, кроме х = 0. Записываем промежутки непрерывности функции: 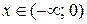 и
и 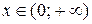 .
.
В точке х = 0 функция имеет разрыв типа "скачок", так как не существует 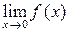 , но при
, но при 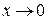 существуют конечные односторонние пределы функции, не совпадающие между собой:
существуют конечные односторонние пределы функции, не совпадающие между собой:
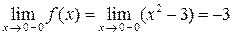 ,
, 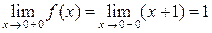 .
.
Ответы:
а) х1 = 0 – точка непрерывности функции 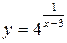 , х2 = 3 – точка
, х2 = 3 – точка
бесконечного разрыва функции, схематический чертеж графика функции
в окрестности точки разрыва на рис. 20;
б) график функции 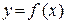 – на рис. 24, промежутки непрерывности функции:
– на рис. 24, промежутки непрерывности функции: 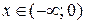 и
и 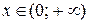 , х = 0 – точка разрыва типа "скачок".
, х = 0 – точка разрыва типа "скачок".
Решение задачи 4
1) Найдем корни уравнения 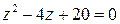 на множестве комплексных чисел:
на множестве комплексных чисел:
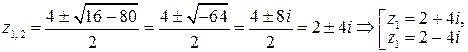
(здесь использовано: 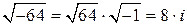 ).
).
2) Чтобы найти комплексное число 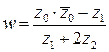 , вычислим сначала
, вычислим сначала 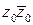 :
:
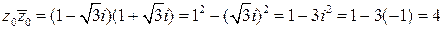 (
( 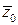 – это число, сопряженное числу
– это число, сопряженное числу 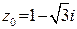 , т. е.
, т. е. 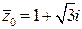 ).
).
Затем находим числитель 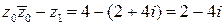 и знаменатель
и знаменатель 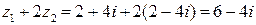 .
.
Теперь вычисляем w, используя домножение числителя и знаменателя на число, сопряженное знаменателю:
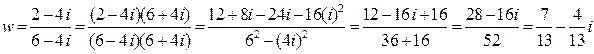 – получили число w в алгебраической форме.
– получили число w в алгебраической форме.
3) Комплексное число 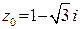 задано в алгебраической форме z0 = x + yi, где x = 1, y =
задано в алгебраической форме z0 = x + yi, где x = 1, y = 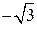 . Получим тригонометрическую форму этого числа z0 = r (cos j + sin j), используя формулы (13) и (14). Вычислим модуль комплексного числа
. Получим тригонометрическую форму этого числа z0 = r (cos j + sin j), используя формулы (13) и (14). Вычислим модуль комплексного числа 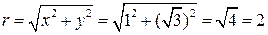 и его аргумент:
и его аргумент:
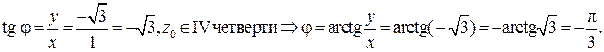
Таким образом, 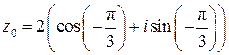 – тригонометрическая форма числа z0.
– тригонометрическая форма числа z0.
Для вычисления 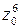 используем формулу (15) возведения комплексного числа в натуральную степень:
используем формулу (15) возведения комплексного числа в натуральную степень:
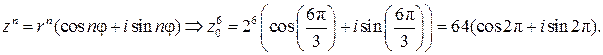
Здесь аргумент 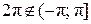 . Выбираем главное значение аргумента, принадлежащее промежутку
. Выбираем главное значение аргумента, принадлежащее промежутку 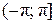 , используя формулу (11):
, используя формулу (11): 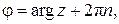
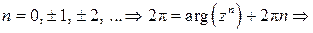 при n = –1 получаем arg ( zn ) = 0. Тригонометрическая форма комплексного числа
при n = –1 получаем arg ( zn ) = 0. Тригонометрическая форма комплексного числа 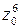 для
для 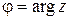 имеет вид:
имеет вид:
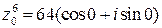 .
.
Подставив значения cos 0 = 1, sin 0 = 0, получим алгебраическую форму этого числа: 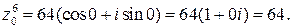
Ответы: 1) 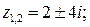 2)
2) 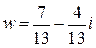 ; 3)
; 3) 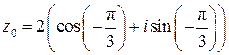 ;
; 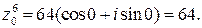
Справочный материал по теме "Дифференциальное исчисление функциЙ одной переменной"
Дифференцирование функций
Производной функции 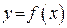 в точке х называется конечный предел отношения приращения функции
в точке х называется конечный предел отношения приращения функции 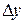 к приращению аргумента Dx:
к приращению аргумента Dx:
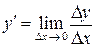 , (16)
, (16)
где 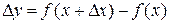 .
.
Другие обозначения производной: 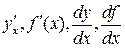 .
.
Если существует производная функции 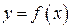 в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной
в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной 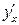 . При дифференцировании используют таблицу производных и правила дифференцирования.
. При дифференцировании используют таблицу производных и правила дифференцирования.
Таблица 3
Таблица производных основных элементарных функций
