Дифференциальное исчисление функции одной переменной.

I. Введение.

В конце второго тысячелетия особенно ясно осознается всеобщая «математизация» человеческой деятельности. Безусловно, такая математизация во многом определяется широким использованием компьютеров. Последние позволили применить математические методы во многих сферах практической деятельности.

Современная экономическая теория включает в себя как необходимый элемент математические методы и модели. Математика, являясь аппаратом количественного расчета, дает также возможность четко сформулировать проблемы.

Можно утверждать, что математика стала элементом общей культуры человечества.

Настоящее пособие знакомит читателя с основными вопросами курса математики, примерами решения задач и вариантами контрольных работ, предлагаемым студентам заочного отделения Ялтинского института менеджмента.

II. Основные вопросы курса «Математика» – первый семестр.

Числа и их графическое изображение.

Понятие числа. Целые числа. Рациональные числа. Иррациональные числа. Действительные числа. Комплексные числа. Действия с комплексными числами. Графическое изображение комплексных чисел.

Исчисление процентов.

Накопление. Дисконтирование. Погашение долгосрочных кредитов. Методы исчисления амортизации.

Векторы.

Понятие векторной величины. Сумма и разность векторов. Произведение вектора на число. Декартова система координат на плоскости и в пространстве. Координаты вектора. Координаты суммы, разности векторов и произведения вектора на число. Координаты точки, делящей отрезок в заданном отношении. Скалярное произведение векторов. Скалярное произведение векторов, заданных своими координатами. Угол между векторами.

Основы матричной алгебры.

Понятие матрицы. Действия над матрицами. Транспонированная матрица. Обратная матрица. Определители. Свойства определителей. Вычисление обратных матриц с помощью определителей. Системы уравнений первой степени. Формулы Крамера. Собственные значения матриц. Векторное произведение. Смешанное произведение и его геометрический смысл.

Аналитическая геометрия на плоскости.

Уравнение линии на плоскости. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в отрезках. Угловой коэффициент прямой. Уравнение прямой, проходящей через данную точку параллельно данному вектору. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение прямой. Угол между двумя прямыми. Расстояние от точки до прямой. Уравнение: окружности, эллипса, гиперболы, параболы.

Функции одной переменной.

Понятие функции. Способы задания функций. Ограниченность, монотонность, четность и периодичность. Обратная функция. Функции наиболее часто встречающиеся в экономических исследованиях. Линейная функция. Графическое решение системы двух уравнений первой степени. Степенная функция. Показательная функция. Логарифмическая функция. Тригонометрические функции.

Последовательности.

Числовые последовательности. Ограниченные и монотонные последовательности. Предел числовой последовательности. Сходящиеся и расходящиеся числовые последовательности. Теоремы о пределах числовых последовательностей. Число е.

Предел функции. Непрерывность функции.

Предел функции в точке. Теоремы о пределах функций. Непрерывность функции в точке. Точки разрыва и их классификация. Первый замечательный предел. Второй замечательный предел.

Дифференциальное исчисление функции одной переменной.

Задачи, приводящие к понятию производной. Производная функции, геометрический смысл производной. Производная суммы, разности, произведения и частного функций. Производная сложной, обратной и параметрически заданной функции. Производные некоторых элементарных функций, таблица производных. Производные высших порядков. Правило Лопиталя. Приложение производной к исследованию функций. Построение графиков функций. Дифференциал функции. Геометрический смысл дифференциала. Приложение дифференциала к приближенным вычислениям.

III. Контрольные вопросы.

В результате изучения теоретических вопросов, предлагаемых к изучению в первом семестре по курсу "Математика" студент должен ответить на следующие вопросы:

1. Как определяется рациональное число?

2. Дайте определение иррационального числа.

3. Дайте определение комплексного числа.

4. Сформулируйте правило сложения комплексных чисел. Как графически изображается операция сложения?

5. Как перемножить два комплексных числа?

6. Как разделить одно комплексное число на другое?

7. Как изображаются комплексные числа?

8. Что такое вектор?

9. Как складывать вектора?

10. Как вычитать вектора?

11. Как изображаются вектора?

12. Как определить проекции вектора на оси координат?

13. Как определить координаты точки, делящей отрезок в заданном отношении?

14. Дайте определение скалярного произведения.

15. Приведите формулу для вычисления скалярного произведения векторов, заданных своими декартовыми координатами.

16. Как определить угол между двумя координатами?

17. Определите размер вклада в банке через n лет при заданной процентной ставке.

18. Опишите расчет погашения долгосрочного кредита.

19. Дайте определение матрицы.

20. Как складывать матрицы?

21. Как перемножать матрицы?

22. Дайте определение транспонированной матрицы.

23. Что называется определителем матрицы?

24. Перечислите свойства определителей.

25. Дайте определение обратной матрицы.

26. Как вычислять обратную матрицу?

27. Сформулируйте правило решения систем линейных уравнений методом Крамера.

28. Сформулируйте правило решения систем линейных уравнений методом Гаусса.

29. Каким уравнением определяется собственное значение матрицы?

30. Как определяется векторное произведение?

31. Как определяется смешанное произведение векторов?

32. Каким уравнением определяется уравнение прямой, проходящей через две заданные точки?

33. Напишите уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору.

34. Напишите уравнение прямой, проходящей через заданную точку, параллельно заданному вектору.

35. Напишите уравнение прямой в отрезках.

36. Как определить угол между двумя прямыми?

37. Как вычислить расстояние от точки до прямой?

38. Напишите уравнение окружности и дайте определение этого множества точек.

39. Напишите уравнение эллипса и дайте определение этого множества точек.

40. Напишите уравнение гиперболы и дайте определение этого множества точек.

41. Напишите уравнение параболы и дайте определение этого множества точек.

42. Перечислите способы задания функции.

43. Определите понятия ограниченности и монотонности функции.

44. Определите понятия четности и периодичности функции.

45. Как определяется обратная функция? Приведите примеры.

46. Нарисуйте графики функций .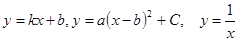

47. Нарисуйте графики функций .

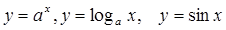48. Нарисуйте графики функций .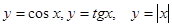

49. Дайте определение числовой последовательности. Что называется ограниченной монотонной последовательностью?

50. Сформулируйте теоремы о пределах последовательностей.

51. Приведите пример числовой последовательности.

52. Число е.

53. Приведите определение производной. Каков геометрический смысл производной?

54. Сформулируйте правило вычисления производной суммы, разности двух функций.

55. Сформулируйте правило вычисления производной произведения двух функций.

56. Сформулируйте правило вычисления производной от частного двух функций.

57. По какому правилу вычисляется производная сложной функции? Приведите примеры.

58. Как вычисляется производная обратной функции? Приведите примеры.

59. Напишите таблицу производных элементарных функций.

60. Сформулируйте правило Лопиталя вычисления пределов.

61. Приведите схему исследования функций.

62. Дифференциал функций. Определение и геометрический смысл.

63. Применение дифференциала к приближенным вычислениям.

64. Теоремы о пределах функций.

65. Первый замечательный предел.

66. Второй замечательный предел.