Дискретная случайная величина

Дискретная случайная величина принимает в результате испытания различные значения, которые можно записать в виде последовательности.

Закон распределения дискретной случайной величины X, принимающей значения с вероятностями p₁, p₂,…, p_n, представим в виде таблицы:

			…
			…

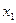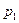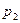Причем должно быть выполнено условие p₁+p₂+…+p_n=1, называемое условием нормировки.

Математическим ожиданием M(X) дискретной случайной величины X называют число M(X)=x₁p₁+x₂p₂+…+x_np_n, где x_i – всевозможные значения случайной величины , p_i – вероятности, соответствующие значениям x_i.

Дисперсией дискретной случайной величины X называют число

D(X) = –M(X))² p_i,

где x_i – всевозможные значения случайной величины X, p_i – вероятности, соответствующие значениям x_i, M(X) – математическое ожидание случайной величины X. Для дискретной случайной величины справедливо равенство:

D(X) =x₁²p₁+x₂²p₂+…+x_n ²p_n–( M(X))².

Пусть проводится n независимых испытаний. Вероятность осуществления события A в одном испытании постоянна и равна p. Дискретная случайная величина X – число испытаний, в которых произошло событие A имеет биномиальное распределение. Это распределение вида

				…
				…

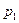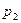Вероятности p_i вычисляют по формуле p_i= pⁱ(1–p)^n-i (i=0,1,…,n). Математическое ожидание M(X) числа появлений события A в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: M(X)=np. Дисперсия D(X) равна произведению числа испытаний на вероятности появления и не появления события в одном испытании: D(X)=np(1–p).

Пример 1. Дискретная случайная величина X задана законом распределения

	0	1	2
	0,3	0,5	?

Найдите: 1) вероятность того, что случайная величина X примет значение, равное двум; 2) математическое ожидание и дисперсию X.

Решение. Неизвестную вероятность P(X=2) вычисляют по формуле:

P(X=2)=1–P(X=0) –P(X=1)=1–0,3–0,5=0,2

Математическое ожидание и дисперсия случайной величины соответственно равны:

M(X)=0∙0,3+1∙0,5+2∙0,2=0,9; D(X)=0²∙0,3+1²∙0,5+2²∙0,2–(0,9)²=0,49.

Ответ: 0,2; 0,9; 0,49.

Пример 2. Независимые дискретные случайные величины X и Y заданы законами распределений:

	0,3	0,7			0,6	0,4

Найдите закон распределения случайной величины Z= X +Y.

Решение. Случайная величина Z=X +Y принимает следующие значения:

z₁=x₁+y₁=1+2=3; z₂=x₁+y₂=1+4=5; z₃=x₂+y₁=3+2=5; z₄=x₂+y₂=3+4=7

с вероятностями:

P(Z=3)=P(X=1)P(Y=2)=0,3∙0,6=0,18;

P(Z=5)=P(X=1)P(Y=4)+ P(X=3)P(Y=2)=0,3∙0,4+0,7∙0,6=0,54;

P(Z=7)=P(X=3)P(Y=4)=0,7∙0,4=0,28.

Закон распределения случайной величины 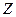имеет вид

	3	5	7
	0,18	0,54	0,28

Ответ:

	3	5	7

Упражнения.

7.5.1. Имеется десять студенческих групп, насчитывающих соответственно 12, 10, 11, 8, 12, 9, 10, 8, 10, 11 студентов. Составьте закон распределения случайной величины , определяемой как число студентов в наугад выбранной группе. Найдите математическое ожидание и дисперсию этой случайной величины.

Ответ:

					12
	0,2	0,1	0,3	0,2	0,2

10,1; 1,89.

7.5.2. Имеется двадцать коробок с яблоками, причем количество яблок в них: 10, 9, 11, 10, 12, 8, 11, 9, 10, 10, 11, 8, 9, 10, 9, 11, 12, 10, 9, 11 штук. Составьте закон распределения случайной величины X, определяемой как количество яблок в произвольно выбранной коробке, и найдите математическое ожидание и дисперсию этой величины. Ответ:

					12
	0,1	0,25	0,3	0,25	0,1

10; 1,3.

7.5.3. Бросают две правильные игральные кости. Случайная величина X –максимальное из двух выпавших очков Найдите математическое ожидание и дисперсию X. Ответ: 4,472; 19,39.

7.5.4. Вероятность попадания в мишень одного стрелка равна 0,5; второго – 0,4. Найдите математическое ожидание и дисперсию общего числа попаданий в мишень. Ответ: 0,9; 0,49.

7.5.5. Из урны, содержащей два белых и три черных шара, наугад вынимают два шара (без возвращения). Найдите математическое ожидание и дисперсию числа вынутых белых шаров. Ответ: 0,8; 0,36.

7.5.6. Вероятность попадания в мишень при каждом из трех выстрелов равна 1/3. Найдите математическое ожидание и дисперсию общего числа попаданий. Ответ: 1; 2/3.

7.5.7. Найдите математическое ожидание и дисперсию числа выпадения герба при десяти независимых бросаниях монеты. Ответ: 5; 2,5.

7.5.8. Найдите математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем вероятность выигрыша по каждому равна 0,3. Ответ: 6.

7.5.9. Найдите математическое ожидание и дисперсию числа бракованных изделий в партии из пяти тысяч изделий, если каждое изделие может оказаться бракованным с вероятностью 0,02. Ответ: 100; 98.

7.5.10. Имеются 4 лампы, каждая из которых с вероятностью 1/3 имеет дефект. При ввинчивании в патрон дефектные лампы сразу перегорают, и тогда ввинчивается следующая. Случайная величина X – число ввинченных ламп. Найдите закон распределения, математическое ожидание и дисперсию случайной величины X. Ответ:

				4
	2/3	2/9	2/27	1/27

40/27; 452/729

7.5.11. Найдите закон распределения случайной величины X, которая может принимать только два значения: x₁ с вероятностью 0,3 и x₂, если известно, что x₁<x₂, M(X)=5,4, D(X)=0,84. Ответ:

		6
	0,3	0,7

7.5.12. Даны все возможные значения дискретной случайной величины X: x₁=1, x₂=2, x₃=3, а также известны M(X)=2,3 и M(X²)=5,9. Найдите закон распределения случайной величины X. Ответ:

			3
	0,2	0,3	0,5

7.5.13. Заданы законы распределения независимых случайных величин X и Y:

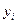	0,2	?	0,4			?	0,4	0,5

Найдите P(X=2), P(Y=0), M(X+Y), M(X–Y), D(X+Y), D(X–Y), M(XY).

Ответ: 0,4; 0,1; 5,2; –0,4; 4; 4; 6,72.

7.5.14. Даны законы распределения независимых случайных величин X и Y:

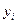	0,1	0,5	?			0,3	?

Найдите P(X=20) и P(Y=20), закон распределения X+Y, проверьте свойство

M(X+Y)=M(X)+M(Y). Ответ: 0,4; 0,7;

				40
	0,03	0,22	0,47	0,28

7.5.15. Случайная величина X задана законом распределения

	-1	0
	0,4	0,6

Случайная величина Y представляет собой число появлений события A с постоянной вероятностью p=0,6 в двух независимых испытаниях. Составьте закон распределения разности X–Y и проверьте свойство дисперсии D(X–Y)=D(X)+D(Y). Ответ:

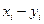	-3	-2	-1	0
	0,144	0,408	0,352	0,096

7.5.16. Независимые случайные величины X и Y заданы законами распределений

	-2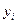
	0,3	0,4	0,3			0,5	0,5

Составьте закон распределения случайной величины Z=2X–Y и проверьте свойство D(2X–Y)=4D(X)+D(Y).

Ответ:

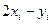	-6	-5	-2	-1		3
	0,15	0,15	0,2	0,2	0,15	0,15

7.5.17. Продаются саженцы трех сортов. Вероятность того, что приживется саженец первого сорта, равна 0,75; второго – 0,7; третьего – 0,6. Садовод купил три саженца различных сортов. Составить закон распределения числа прижившихся у него саженцев.

7.5.18. В бригаде имеется четыре трактора. Вероятность выхода в поле каждого из них каждый день одинакова и равна 0,8. Составить закон распределения случайной величины – числа тракторов, которые выйдут в поле в произвольно выбранный день.

7.5.19. Вероятность поражения вирусным заболеванием куста земляники равна 0,3. Составить закон распределения числа кустов земляники, зараженных вирусом из четырех посаженных. Найти функцию распределения и построить ее график.

7.5.20. Доярка обслуживает три доильных аппарата. Вероятность того, что в течении дойки первый аппарат не потребует ее внимания, равна 0,1; второй – 0,2; третий – 0,3. Составить закон распределения числа доильных аппаратов, которые потребуют внимания рабочего в течении часа.

7.5.21. Вероятность повреждения упаковки при перевозке изделия равна 0,2. Составить закон распределения числа изделий с поврежденной упаковкой среди взятых наудачу четырех. Найти функцию распределения этой случайной величины и пользуясь ею, найти вероятность того, что изделий с поврежденной упаковкой будет не меньше одного, но меньше трех.