Метод эквивалентного генератора

Методом эквивалентного генератора определяют ток только в одной ветви сложной электрической цепи.

Часть электрической цепи с источниками питания, имеющая два вывода называется активным двухполюсником. Условное изображение активного двухполюсника:

Напряжение между разомкнутыми выводами активного двухполюсника называют напряжением холостого хода активного двухполюсника - U_abxx.

Эквивалентное сопротивление активного двухполюсника при отсутствии в нем источников питания (если источник имеет внутреннее сопротивление, это сопротивление оставляют) называют входным сопротивлением активного двухполюсника – R_вх .

Чтобы найти ток методом эквивалентного генератора необходимо:

а) Разбить цепь на исследуемую ветвь и активный двухполюсник.

б) Определить напряжение холостого хода (U_abxx.) и входное сопротивление активного (R_вх) двухполюсника.

в) По формуле эквивалентного генератора определить ток в исследуемой ветви: I_i= U_abxx./(R_вх + R_i)

г) Если исследуемая ветвь имеет источник питания, то ток определяют по формуле: I_i= (U_abxx. ± E_i)/(R_вх + R_i)

где Е_i-ЭДС источника питания в i -той ветке. ЭДС имеет знак плюс, если направление тока совпадает с направлением ЭДС, и знак минус, если их направления противоположны.

ПОТЕНЦИАЛЬНАЯ ДИАГРАММА

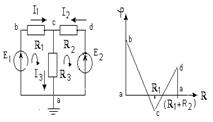
Потенциальной диаграммой называют график зависимости распределения потенциала электрической цепи от сопротивления участков этой цепи: . Чтобы построить потенциальную диаграмму, потенциал какой-либо точки приравнивают к нулю (заземляют) и определяют потенциалы остальных точек как напряжение между данной точкой и точкой нулевого потенциала. График имеет вид ломаной линии. При построении диаграммы необходимо учитывать, что источник повышает потенциал на величину ЭДС в направлении действия источника и уменьшает его на эту же величину в обратном направлении. Ток на участке цепи с сопротивлением направлен в сторону понижения потенциала. Потенциалы начальной и конечной точек замкнутого контура равны нулю.

График потенциальной диаграммы позволяет определить напряжение между любыми точками цепи; найти точки равного потенциала; по углу наклона прямых судить о силе тока на разных участках. Пример построения потенциальной диаграммы представлен на рисунке.

10.ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Рассмотрим цепь с последовательно соединенными активным сопротивлением - R , индуктивностью – L и емкостью – С.

Для векторов действующих напряжени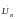й , и запишем второй закон Кирхгофа:

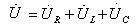
Складывая эти вектора графически и, учитывая, что вектор напряжения на активном сопротивлении - 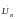совпадает по фазе с вектором тока, вектор напряжения на индуктивности - опережает ток на угол π/2, а вектор напряжения на емкости - отстает от вектора тока на угол π/2, получим прямоугольный треугольник напряжений, гипотенуза которого равна полному напряжению - 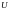, а катеты равны активному напряжению - и реактивному напряжению - ( ) :

Из треугольника напряжений видно, что:

Если разделить все стороны прямоугольного треугольника напряжений на общий ток 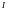, то получим подобный ему треугольник сопротивлений, гипотенуза которого равна полному сопротивлению цепи - 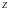, а катеты - активному и реактивному сопротивлению цепи - и ( ) :

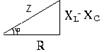
Из этого треугольника можно найти полное сопротивление цепи 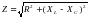и записать закон Ома для цепи переменного синусоидального тока: