Продолжения операторов и функционалов

Комментарий. Рассмотрим для определённости банаховы пространства. Если оператор определён не на всём банаховом пространстве 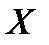, а на линейном многообразии , то можно ли его продолжить на всё пространство, то есть можно ли построить новый оператор, совпадающий со старым на многообразии и сохраняющий какие-то его свойства на всём банаховом пространстве 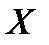? Для линейных операторов имеет место

Теорема. Пусть 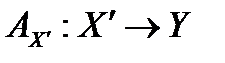непрерывный линейный оператор, заданный на всюду плотном линейном многообразии банахова пространства , где 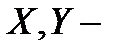банаховы пространства. Тогда существует непрерывный линейный оператор 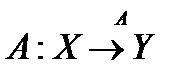, причём 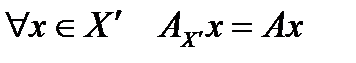, а нормы этих операторов совпадают, то есть .

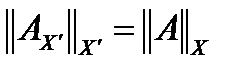Пусть 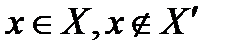. Поскольку линейное многообразие 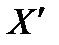всюду плотно в пространстве 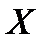, то 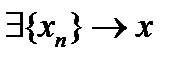, причём 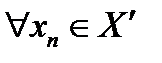(по определению всюду плотного множества). То есть последовательность 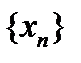фундаментальна, а тогда 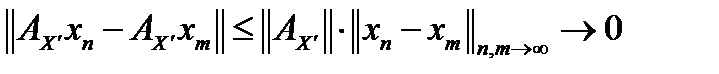. Но тогда и последовательность 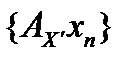фундаментальна, а пространство банахово, то есть полное и поэтому последовательность 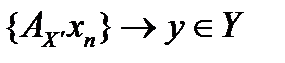. Положив 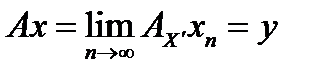, мы определим некоторый оператор .

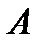Однако, линейный непрерывный функционал можно продолжить без изменения нормы, даже если он первоначально задан не на всюду плотном линейном многообразии банахова пространства.

Определение 1. Вещественный функционал 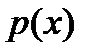, заданный на вещественном линейном пространстве 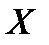, называется однородно-выпуклым (полунормой) , есл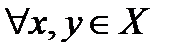и и 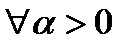верно, что 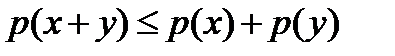и .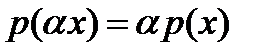

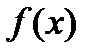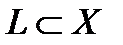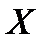
Определение 2. Пусть функционал задан на линейном многообразии , где линейное нормированное пространство. Вещественный функционал 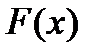есть продолжение функционала 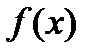, если .

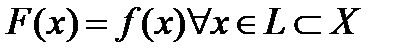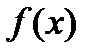Теорема 1 (Принцип продолжения Хана Банаха). Пусть линейный непрерывный функционал задан на линейном многообразии 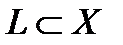, где 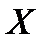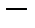линейное нормированное пространство, причём на линейном нормированном пространстве 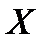задан однородно-выпуклый функционал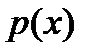 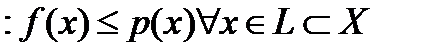. Тогда функционал 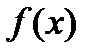можно продолжить на всё пространство 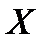, причём для продолжения 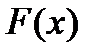выполнено, что .

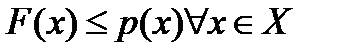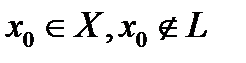Пусть . Для любого действительного 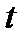рассмотрим множество .

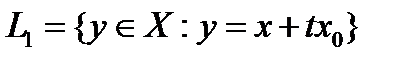1. Покажем, что это множество есть линейное многообразие, причём любой элемент из него имеет однозначное представление.

Пусть для любого действительного 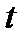существует элемент 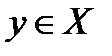, имеющий два представления 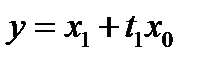и 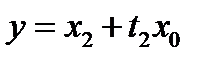. Если 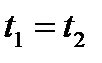, то и 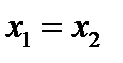. Если 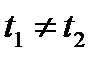, то 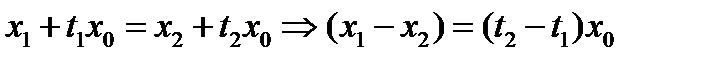, то есть 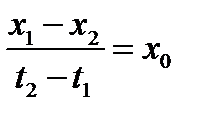. Но 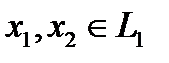, то есть и 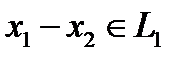, а, следовательно, и левая часть принадлежит 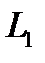, но 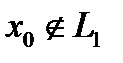. Очевидно, что 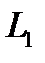есть линейное многообразие, так как 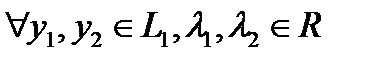имеем .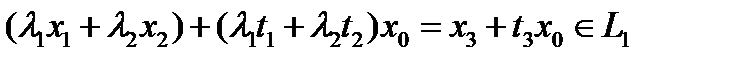

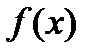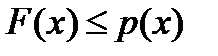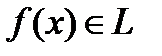2. Сформулируем требования, которым должен удовлетворять функционал , чтобы его продолжение удовлетворяло неравенству . Пусть каким либо образом удалось получить продолжение функционала на 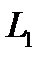, причём так, что выполняются условия теоремы:

1. 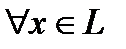выполнено 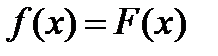и 2. 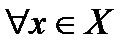выполнено 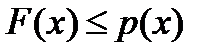. Тогда 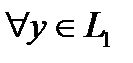можно записать, что 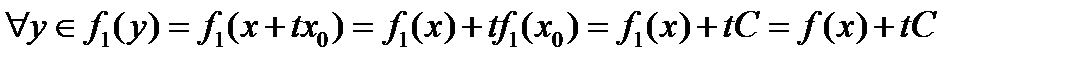( 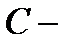значение функционала в точке 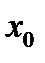, а 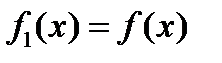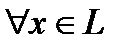). Таким образом, любой линейный функционал, продолжаемый с линейного многообразия 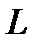на линейное многообразие 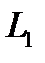должен иметь вид 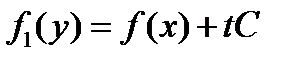, где 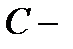константа. Но для того, чтобы сохранялись свойства, надо показать, что 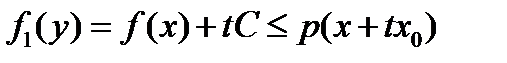. Рассмотрим два случая.

1) Пусть 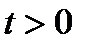. Разделив на 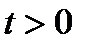, получим 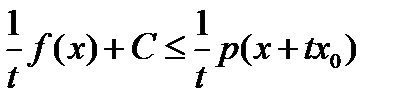. Тогда в силу линейности функционала 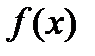, , 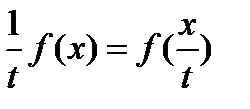а из первого свойства полунормы 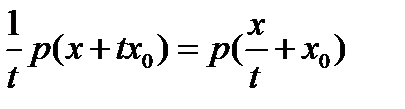, то есть 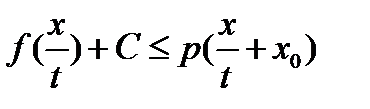.Так как 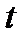произвольное, то 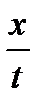произвольный элемент из 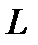. Обозначив его через 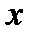, сразу получим .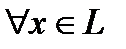

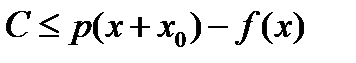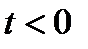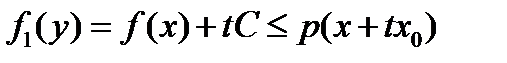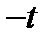2) Пусть . Разделив неравенство на , получим 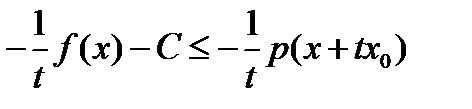. Обозначим 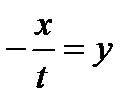. Теперь 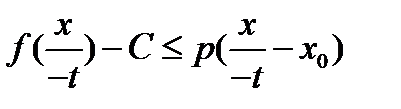, то есть 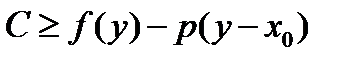. Итак, если мы хотим, чтобы продолжение удовлетворяло неравенству 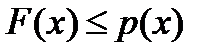, нужно показать, что 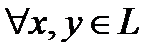константу С, определяющую продолжение, всегда можно выбрать так: .

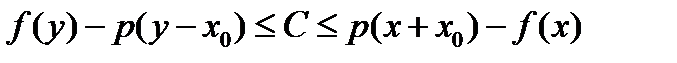Рассмотрим 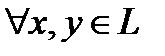соотношение . Так как это условие выполняется , в том числе и для супремума и инфинума, то . Таким образом, константу С, удовлетворяющую условию теоремы, следует выбрать так: .

1. Опишем завершение доказательства. Если 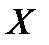сепарабельное банахово пространство, то в нём существует счётное всюду плотное множество 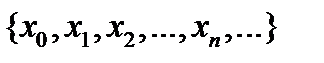. Матиндукцией осуществляем продолжение, последовательно присоединяя к 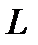те элементы, которых там нет. В результате мы получим продолжение функционала на всюду плотное линейное многообразие 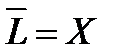. Дальше, как указано в комментарии, продолжение функционала осуществляется по непрерывности: 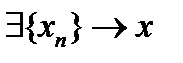, причём все 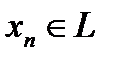, , 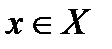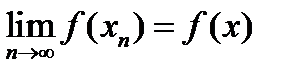. Если пространство не сепарабельно, но банахово, то доказательство завершается методом трансфинитной индукции, обобщающим метод математической индукции на несчётные множества.

Примерно в этом месте в основном и заканчивается ликбез и начинается то, что математики называют функциональным анализом.

КУЛЬТУРНЫЙ МИНИМУМ.

1. Что такое линейный оператор? Примеры.
2. Что такое ограниченный линейный оператор? Понятие нормы.
3. Какой оператор называется непрерывным в точке,на D(A)? Все определения.
4. Принцип открытости отображений Банаха. Идея доказательства.
5. Что такое равномерная и поточечная (сильная)сходимость последовательности НЛО 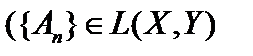к оператору ?
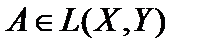6. Какой оператор называется сжимающим? Что такоенеподвижная точка оператора?
7. Какой оператор называется обратимым,непрерывно обратимым? Что такое ядро и образ оператора? Какой оператор называется вырожденным?
8. Какая задача называется корректной по Адамару?
9. Какой оператор называется замкнутым? Теорема о пришельцах.
10. Что такое график линейного оператора?
11. Какой оператор называется компактным?
12. Какой операторназывают сопряженным к оператору 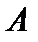? Какие операторыназывают самосопряжёнными и нормальными?

ВОПРОСЫ.

1. Доказать, что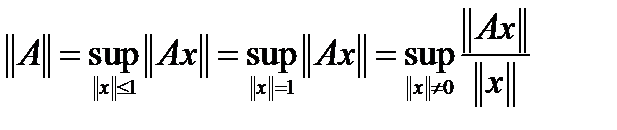

2. Доказать, что оператор дифференцирования не ограничен в пространствах 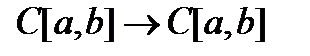и ограничен в пространствах .

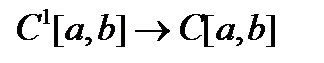3. Доказать критерий непрерывности линейного оператора, как непрерывного в нуле.

4. Доказать критерий непрерывности линейного оператора, как ограниченного.

5. Доказать, что замыкание образа окрестности нуля в пространстве 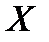содержит в себе некоторую окрестность нуля в пространстве .

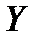6. Доказать, что образ окрестности нуля в пространстве 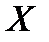содержит в себе некоторую окрестность нуля в пространстве .

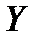7. Доказать принцип открытости отображений Банаха.

8. Доказать, что пространство 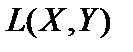есть нормированное пространство с нормой .

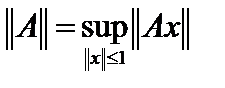9. Доказать, что пространство 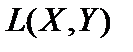банахово в смысле равномерной сходимости.

10. Доказать, что пространство 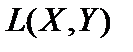банахово в смысле поточечной сходимости.

11. Доказать принцип равномерной ограниченности Банаха Штейнгауза.

12. Доказать принцип сжимающих отображений Банаха.

13. Доказать теорему о линейности обратного оператора.

14. Критерий обратимости линейного оператора, как невырожденного. Контрпример.

15. Критерий существования и непрерывности обратного оператора.

16. Доказать теорему Банаха о гомеоморфизме.

17. Доказать теорему Банаха о замкнутом графике.

18. Доказать критерий замкнутости линейного оператора.

19. Доказать, что компактный оператор 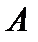всегда ограничен.

20. Теорема о коразмерности ядра ненулевого непрерывного функционала .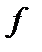

21. Теорема о связи непрерывности функционала и замкнутости его ядра.

22. Теорема Рисса об общем виде линейного непрерывного функционала.

23. Доказать принцип продолжения Хана 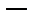Банаха.

ЗАДАЧИ.

1. Линейный функционал в 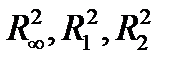в точках (1,2) и (3,4) равен 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.

2. Найти норму преобразования .

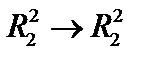3. Найти норму преобразования .

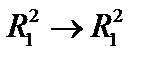4. Найти норму преобразования .

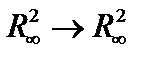5. Показать, что оператор Фредгольма непрерывен в пространстве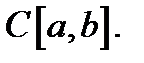

6. Показать, что оператор Фредгольма непрерывен в пространстве .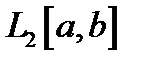

7. Является ли сжимающим отображение 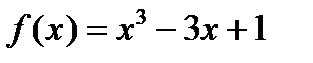на отрезке ?

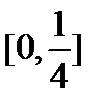8. Является ли отображение 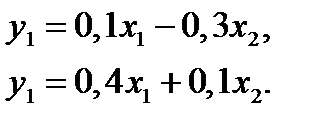сжимающим в ?

9. При каких 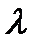оператор Фредгольма 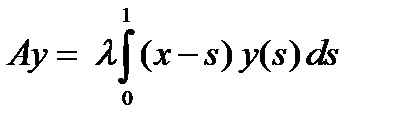является сжимающим при действии ;

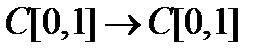10. При каких 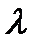оператор Фредгольма 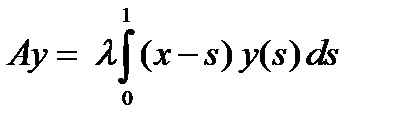является сжимающим при действии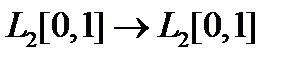

11. При каких 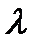оператор Вольтерра 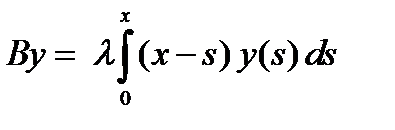является сжимающим при действии .

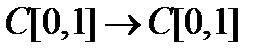12. Показать, что оператор интегрирования на паре пространств 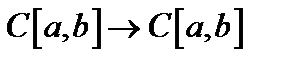замкнут.

13. При каких 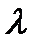оператор Вольтерра 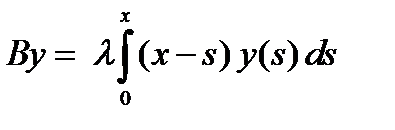является сжимающим при действии .

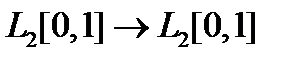14. Показать замкнутость оператора дифференцирования при действии .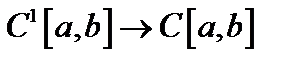

15. Существует ли оператор, обратный к оператору дифференцирования?

16. Показать, что единичный оператор 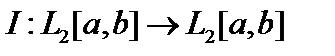ограничен, но не компактен.

17. Найти оператор, сопряженный к оператору Фредгольма.

18. Найти оператор, сопряженный к оператору 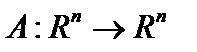.