Таким образом, база результирующего сигнала
Рис. 4.1.
На рис.3.1, б представлены сечения ФН плоскостями, параллельными плоскости t0F. Сплошной линией проведены сечения для сигнала с длительностью t01, а пунктирной линией – сечения для сигнала с длительностью t02 (t02>t01). Справа от каждого сечения показано значение /c(t, F)/, на уровне которого взято это сечение, слева даны значения /c(t, F)/2. Сечения ФН простого сигнала с гауссовой огибающей представляют собой эллипсы.
Из рис.3.1, б следует, что изменение длительности сигнала (сравните сплошные кривые и пунктирные) приводит только к изменению соотношения между полуосями эллипсов. При уменьшении t0ФН сжимается по оси t(увеличивается FЭ), но во столько же раз расширяется по оси F (уменьшается ТЭ), т.е. увеличение разрешающей способности по дальности приводит к эквивалентному ухудшению разрешения по скорости. Это вызвано тем, что для простых сигналов ТЭ и FЭжёстко связаны друг с другом d = ТЭ × FЭ = 1 , и увеличение ТЭ или FЭнеминуемо приводит к уменьшению Df и tu.
Рассмотрение ФН простого радиоимпульса с прямоугольной огибающей приводит к такому же выводу: сжатие ФН по координате tвызывает её эквивалентное растяжение по координате F и наоборот.
4.2. Оценка потенциальной разрешающей способности
Задача разрешения нескольких целей обычно решается после задачи обнаружения (иногда вместе с ней). В этом случае интересующие нас Dt и Dfд выражают соответственно временной и частотный сдвиги между принятыми сигналами, то есть
Dt = t1 – t2 = tR 1– tR2 ,
Dfд = DFд = (f0 ± Fд1) – (f0 ± Fд2) = Fд1 ± Fд2 ,
где tR1 и tR2 – время запаздывания сигналов, отражённых от 1-й и 2-й целей соответственно; Fд1 и Fд2 – частотный сдвиг несущих колебаний сигналов за счёт эффекта Доплера у 1-й и 2-й целей соответственно. Чтобы оценить потенциальную разрешающую способность по параметру разрешения Da (Da = Dt или Da = Dfд, – рис.1.1 и рис.1.2), нужно, прежде всего, установить, какие сигналы считаются разрешимыми, а какие – неразрешимыми. Для этого рассмотрим зависимость формы выходного сигнала амплитудного детектора, подключенного к выходу СФ. Этот сигнал является суммой двух перекрывающихся входных сигналов с прямоугольными огибающими. Мы рассмотрим только простейший случай сигнала на выходе амплитудного детектора, являющегося суммой двух одинаковых входных сигналов (рис.1.1). Из сопоставления рис.1.1 а, б, в видно, что при сдвигах Da1 > Da2 суммарный сигнал будет иметь двугорбый вид, а при сдвигах Da3 £ Da2 имеет место одногорбая кривая. Двугорбая кривая по критерию Релея всегда допускает уверенное разрешение, а одногорбая не позволяет разрешить эти сигналы. Поэтому наименьший допустимый сдвиг сигналов по разрешаемому параметру должен быть равен ширине выходного сигнала по этому параметру, то есть АКФ входного сигнала, отсчитанной на уровне 0,5 /c(0, 0)/. Эта ширина и будет оценкой потенциальной разрешающей способности при приёме двух одинаковых сигналов.
На рис. 4.2, а показаны сечения ФН трёх отражённых сигналов (на уровне 0,25 /c(0, 0)/2 или 0,5 /c(0, 0)/ сечения приблизительно соответствуют прямоугольным импульсам). Цель 1 неподвижна (Fд1 = 0) и находится на некоторой дальности R = ctR1 / 2. Цель 2 – на той же дальности, но движется (приближается, DFд > 0). Цель 3 – неподвижная, на большей дальности. Видно, что поскольку сечения ФН касаются, то цели разрешаются: 1 и 3 – по дальности, 1 и 2 – по скорости, 2 и 3 – по обоим параметрам. Разрешающая способность по дальности (DR) пропорциональна Dt, по скорости (DVr) пропорциональна DFд. В дальнейшем, опуская коэффициент пропорциональности, мы величину Dt будем часто обозначать как DR, а DFд – как DVr (рис.4.2). Поскольку мы приняли уровень сечения 0,25 /c(0, 0)/2 (или 0,5 /c(0,0)/), то Dt = tu. Аналогично DFд = Df. Возьмём теперь более короткий импульс (с более широким спектром). На рис.4.2, б показаны сечения ФН для этого случая (цели 1, 4, 5). Теперь DR, пропорциональное Dt, уменьшилось, а DVr, пропорциональное DFд, во столько же раз возросло.
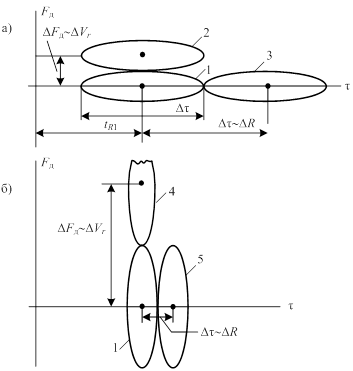
Рис. 4.2.
4.3. Сложный сигнал с линейной частотной модуляцией
Условия (3.9) и (3.10) накладывают требования только на высоту главного пика (/c(0, 0)/ =1), и объём ФН (VФH= 1). На форму ФН никаких требований не накладывается, её мы можем менять по своему усмотрению (а после этого подбирать сигнал под выбранную форму ФН). Например, мы можем переносить ФН относительно осей координат. При этом, как видно из рис.4.3, сечение ФН оказывается малым в направлениях, как оси t(см. Dt), так и Fд(см. DFд). Это даёт возможность получить одновременно хорошую разрешающую способность как по дальности (DR ~ Dt между целями 1 и 3), так и по скорости (DVr ~ DFд между целями 1 и 2). В то же время длительность сигнала tu, если судить о проекции ФН на ось t, оказывается большой. Велика и ширина спектра df, определяемая проекцией ФН на ось частоты f. Для простого сигнала база сигнала определялась произведением осей эллипса tu и Δf
d = t×Δf = 1.
Здесь жебаза сигнала
d1 = tu× df >> 1 = tu× Δf = d,
и d1 больше d во столько раз, во сколько площадь прямоугольника со сторонами tu и df больше площади эллипса, изображающего сечение ФН.
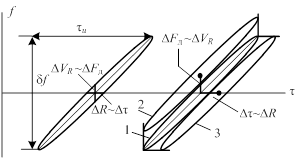
Рис.4.3.
ФН, показанная на рис.4.3, соответствует сигналу в виде длинного импульса с линейной частотной модуляцией (ЛЧМ) в случае, когда частота внутри импульса растёт от начала к концу. Это следует из того, что мгновенная частота спектра f, соответствующая большой оси эллипса, растёт с увеличением временного сдвига t.
Сложный ЛЧМ сигнал записывается
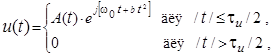
где 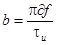 ; df – девиация частоты. Если девиация частоты
; df – девиация частоты. Если девиация частоты 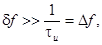 то ширина спектра уже определяется не Δf, то есть не длительностью импульса tu, а девиацией df, которая может быть очень большой. Рис.4.3 указывает только на возможность получения от ЛЧМ сигнала хорошей разрешающей способности по дальности и скорости, но ничего не говорит о том, как эту возможность превратить в действительность. Для этого необходимо осуществить сжатие ЛЧМ сигнала по времени и по спектру.
то ширина спектра уже определяется не Δf, то есть не длительностью импульса tu, а девиацией df, которая может быть очень большой. Рис.4.3 указывает только на возможность получения от ЛЧМ сигнала хорошей разрешающей способности по дальности и скорости, но ничего не говорит о том, как эту возможность превратить в действительность. Для этого необходимо осуществить сжатие ЛЧМ сигнала по времени и по спектру.
Сжатие по времени – получение из длинного сложного сигнала короткого простого – осуществляется СФ, на выходе которого получается развертка во времени корреляционной функции входного сигнала. Один из возможных вариантов построения СФ для ЛЧМ сигнала на линии задержки с неравномерно расположенными отводами показан на рис. 2.3. Там же поясняется его принцип действия.
Второй способ сжатия ЛЧМ импульса реализуется с помощью дисперсионной линии задержки, т.е. такой, в которой скорость распространения колебаний различных частот оказывается различной (например, низкие частоты задерживаются больше высоких – зеркально по отношению к сигналу). Во входном ЛЧМ импульсе ни в один из моментов спектральные составляющие не совпадают по фазе (хотя и связаны определённым законом по фазе), поэтому и их сумма нигде не оказывается большой. Однако за счёт дисперсии все спектральные составляющие задерживаются по-разному, причём так, что на входе дисперсионной линии задержки в некоторый момент оказываются синфазными, образуя короткий сжатый импульс большой амплитуды.
Повышение разрешающей способности по дальности по сравнению
с простым сигналом той же длительности показано на рис. 4.4.
На рис. 4.4, а приведены два перекрывающихся по времени импульса А и Б. Если эти сигналы простые, то на выходе СФ они дают отклики (рис.4.4, б), и цели не разрешаются. Если А и Б – сложные ЛЧМ сигналы, то на выходе СФ два сигнала будут наблюдаться раздельно, следовательно, цели, от которых они отражены, разрешаются (рис.4.4,в). При сжатии ширина спектра не меняется, так как все спектральные составляющие проходят на выход на равных правах. Длительность же выходного сигнала СФ, измеряемая по длительности его центрального пика, уменьшается до t2. Сигнал становится простым, таким, что у него база
d = t2×Df =1.
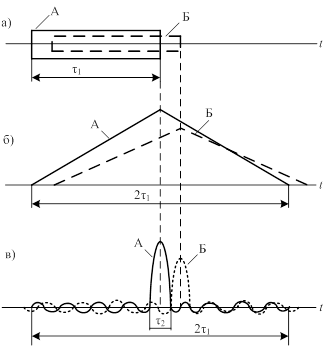
Рис. 4.4.
До сжатия база сигнала
d1 = t1 × df >> 1.
Коэффициент сжатия
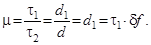
В силу закона сохранения энергии импульсов на входе Е1 и выходе Е2 согласованного фильтра
P2 × t2 = P1 × t1,
откуда
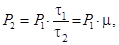
т.е. мощность сжатого импульса в m раз превосходит мощность несжатого, а напряжение – в 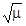 раз. Шумы, проходящие через линию задержки, не сжимаются, так как случайные фазовые соотношения в спектре шумов не перестают быть случайными из-за того, что линия внесёт в них те изменения, которые она вносит в сигнал. Поэтому отношение сигнал-шум (по мощности) возрастает в m раз, отчего дальность действия возрастает в
раз. Шумы, проходящие через линию задержки, не сжимаются, так как случайные фазовые соотношения в спектре шумов не перестают быть случайными из-за того, что линия внесёт в них те изменения, которые она вносит в сигнал. Поэтому отношение сигнал-шум (по мощности) возрастает в m раз, отчего дальность действия возрастает в 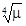 раз.
раз.
Итак, в канале дальности длинный сложный сигнал превращается в короткий простой, что с помощью ФН поясняется на рис. 4.5. ФН сложного сигнала "1" "проектируется" на ось F, отчего ширина ФН вдоль оси t оказывается малой.
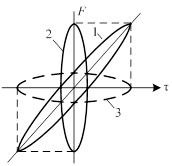
Рис. 4.5.
Для разрешения противоречия между ΔR и ΔVr эту же ФН необходимо "спроектировать" на ось t. Эта операция называется сжатием по спектру (получение из длинного сложного сигнала простого сигнала такой же длительности) и осуществляется демодулятором. Получить из длинного ЛЧМ сигнала длинный простой можно путём устранения ЧМ модуляции, т.е. демодуляцией, которая поясняется с помощью рис.4.6. Здесь на плоскости время-частота пунктирным эллипсом 0 показано сечение центрального пика ФН зондирующего ЛЧМ сигнала с длительностью t1 и девиацией df плоскостью, параллельной плоскостиt, F, 0.
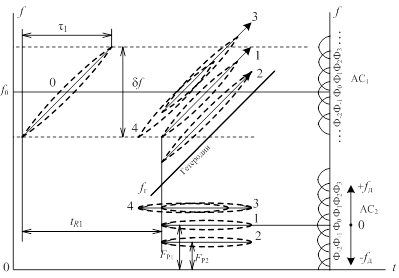
Рис. 4.6.
Наклонные прямые 1, 2, 3, 4 – законы изменения частоты отражённых ЛЧМ сигналов (рис. 4.6). Цель 1 – неподвижная на дальности tR1, цели 2 и 3 – на той же дальности, но 2 – удаляется, а 3 – приближается, поэтому законы изменения частоты этих сигналов сдвинуты относительно сигнала от цели 1 эффектом Доплера вниз и вверх соответственно. Если бы мы попытались принятые сигналы, отраженные от целей 1, 2, 3, подать непосредственно на анализатор спектра АС1, состоящий из набора фильтров ... , Ф-2, Ф-1,Ф0, Ф1, Ф2, Ф3,... , то разрешения по скорости не получилось бы: все сигналы 1, 2, 3 приходили бы в каждый из фильтров, так как все сигналы перекрываются друг с другом по спектру. Задача демодуляции состоит в том, чтобы сузить спектры 1, 2, 3 так, чтобы они не перекрывались.
Для демодуляции используется гетеродин с программированной перестройкой, частота fг которого меняется со скоростью, такой же, что и частота внутри ЛЧМ импульса (прямые fг и 1, 2, 3 параллельны). В силу параллельности прямых разностные частоты FP1, FP2, ... между сигналами гетеродина и отражёнными сигналами оказываются постоянными во времени (ФН проектируется на ось t), т.е. сигналы становятся простыми и узкополосными, и теперь каждый из них целиком находится в полосе пропускания одного какого-либо фильтра из группы фильтров АС2. Номер фильтра, на выходе которого появляется сигнал, является мерой допплеровской частоты и скорости. Фильтр, через который проходит сигнал неподвижной цели, имеет нулевой номер (Ф0), фильтры с положительными номерами соответствуют приближающимся целям, с отрицательными – удаляющимся.
Отметим один недостаток ЛЧМ сигнала: возможность преобразования дальномерной информации в скоростимерную и наоборот. На рис.4.6 пунктиром показано сечение центрального пика ФН сигнала, отраженного от цели 4, которая, как и цель 1, неподвижна (не сдвинута ни вверх, ни вниз по оси f), но находится на дальности меньшей, чем цель 1. После демодуляции сигнал, отраженный от цели 4, попадает в тот же фильтр, что и сигнал, отраженный от цели 3, которая движется (приближается). Так различие между 1 и 4 по дальности преобразовалось в различие между ними по скорости. Не вдаваясь в подробности, можно сказать, что это – следствие того, что мы два неизвестных R и ΔVr пытаемся найти из одного уравнения (уравнения прямой ЛЧМ). Для отыскания двух неизвестных нужна система из двух уравнений (причём, независимых). Рис.4.7 иллюстрирует эту идею.
Создаются два сигнала, ФН которых (1 и 2) перекошены в разные стороны. Положением цели на плоскости (t, F)является область пересечения двух ФН (графическое решение системы двух уравнений путём отыскания точки пересечения прямых, изображающих каждое из уравнений). Сигналы 1 и 2 отличаются направлением ЛЧМ: в первом от начала импульса к концу частота растет, во втором – падает. Такие сигналы можно создавать либо одновременно двумя передатчиками, либо поочередно одним.
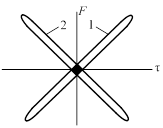
Рис. 4.7.
4.4. Фазоманипулированные сигналы
4.4.1. Краткие сведения о сложных фазоманипулированных сигналах
Сложный сигнал можно сформировать не только методом частотной модуляции, но и методом фазовой манипуляции (ФМ). При этом в качестве строительного элемента (символа) берется короткий прямоугольный радиоимпульс (простой сигнал), а результирующий ФМ сигнал оказывается набором простых сигналов, фаза которых от символа к символу меняется скачком. В общем случае величина скачка фазы может быть произвольной. Ограничимся изучением ФМ сигналов, фаза символов которых принимает лишь два дискретных значения: 0° и 180° (0 и p). На рис. 4.8, а показан простой сигнал длительностью t1и шириной спектра Df1 = 1/t1. На рис. 4.8, б пять простых сигналов составляют сложный. Первый символ сложного сигнала по фазе совпадает с начальной фазой первого простого импульса. Обозначим его фазу как 0. Второй символ стоит вплотную к первому и перевернут по фазе (p), третий и четвёртый имеют ту же фазу, что и первый, и т.д. В результате создается кодовое слово из 5-ти символов со следующим кодом: 0p00p. В дальнейшем при отображении ФМсигналов будем пользоваться более удобным изображением на рис. 4.8, в.
Если бы все N символов имели одинаковую с первым символом фазу, то суммарный сигнал был бы по-прежнему простым, только более длинным. Спектр его сузился бы в N раз, так как t2 = Nt1 и 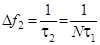 . Если фазы символов чередовать периодически, то мы получили бы периодическую последовательность импульсов, спектр которой тоже был быпериодическим, не сплошным. Можно, однако, так подобрать последовательность символов, что спектр останется широким (Δf2 = Δf1) и сплошным. Длительность же t2возрастает в N раз.
. Если фазы символов чередовать периодически, то мы получили бы периодическую последовательность импульсов, спектр которой тоже был быпериодическим, не сплошным. Можно, однако, так подобрать последовательность символов, что спектр останется широким (Δf2 = Δf1) и сплошным. Длительность же t2возрастает в N раз.
Таким образом, база результирующего сигнала
d2 = t2 ∙Df2 = Nt1∙Df1 =N >>1,
т.е. сигнал действительно отвечает определению сложного сигнала.
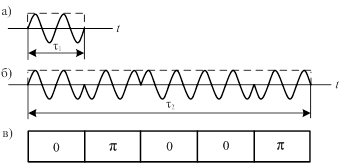
Рис.4.8.
