Холецкий әдісімен танысу

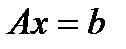(10.1)

Матрицалық түрде жазылған сызықты теңдеулер жүйесін қарастырайық, мұндағы 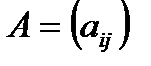- квадратты матрица 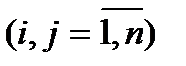және

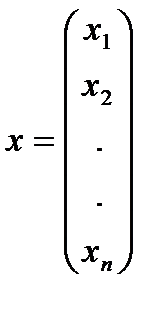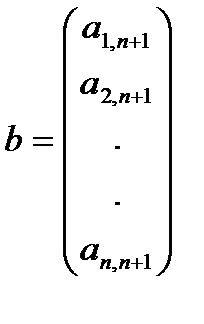, - вектор бағаналар.

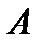матрицасын 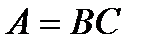көбейтіндісі түрінде өрнектейтін, мұндағы

= , =

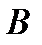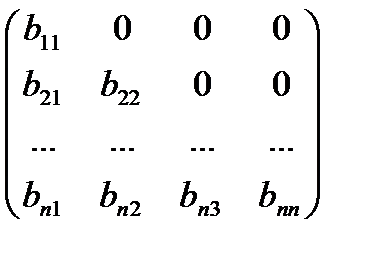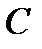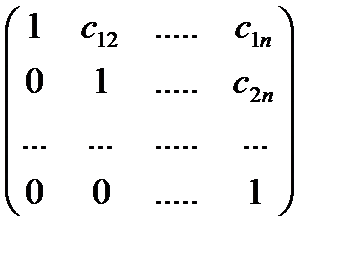
Олай болса 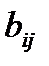және 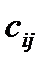элементтерін төмендегі формула бойынша анықтауға болады:

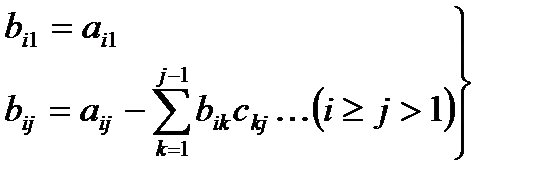(10.2)

және 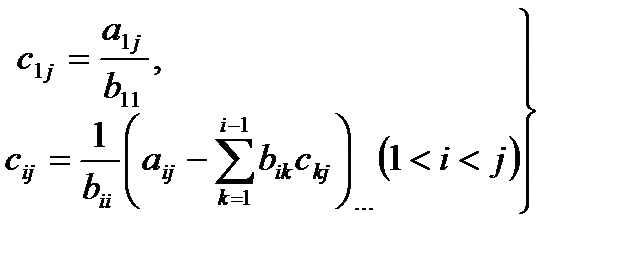(10.3)

Онда ізделінді 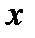векторын

(10.4)

теңдеулер тізбегінен есептеуге болады.

Ал және 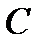матрицалары үшбұрышты болғандықтан, (10.4) жүйелерді шешу қиынға соқпайды:

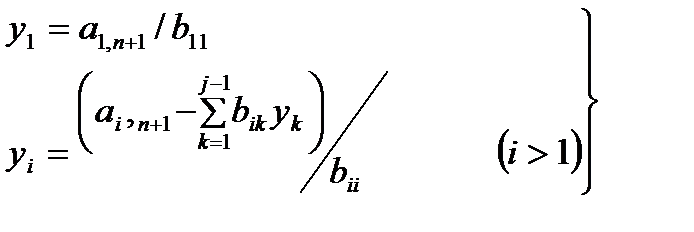(10.5)

және 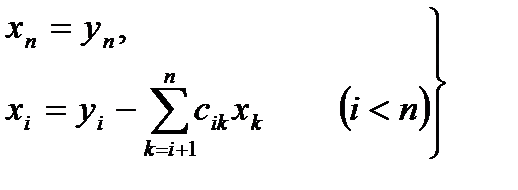(10.6)

(10.5) формуладан 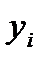сандарын 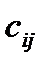коэффиценттерімен бірге есептеу тиімді екенін көреміз. Мұндай есептеу схемасы Халецкий схемасы деп атлады. Схемада әдеттегідей қосып отыру арқылы бақылау жүргізуге болады.

Билет №12

Жай итерация әдісі

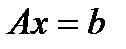(11.1)

теңдеуін, мұндағы 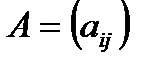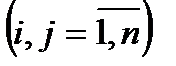- квадратты ерекше емес матрица, келесі түрде жазайық:

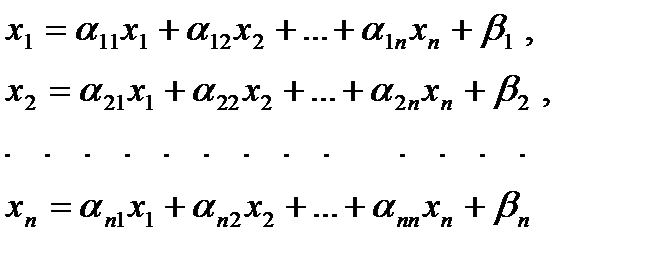(11.2)

немесе қысқаша

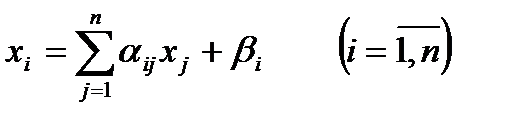
(11.2) жүйенің оң жақтағы 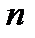-өлшемді векторлық кеңістіктің 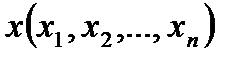нүктесін осы кеңістіктегі нүктесіне түрлендіретін қандайда-бір F бейнесін анықтайды:

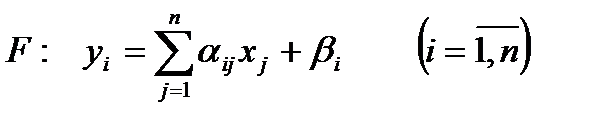(11.3)

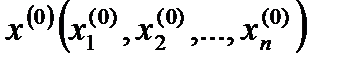бастапқы нүктесін таңдай отырып (11.2) жүйесінің көмегімен 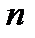-өлшемді кеңістіктегі нүктелердің итерациялық тізбегін құруға болады:

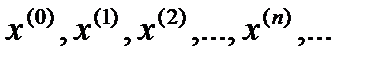(11.4)

Бірінші лекцияда метрика ұғымын ендірген болатынбыз. r матрикасы ендірілген жиын метрикалық кеңістікке айналатыны белгілі.

def 11.1 Егер 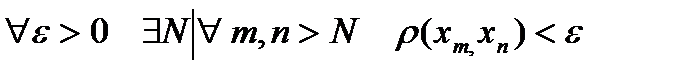теңсіздігі орындалса, онда метриналық кеңістіктің мұндай нүктелер тізбегі фундаменталды деп аталады.

def 11.2 Егер ондағы кезкелген фундаменталды тізбек жинақты болса, онда мұндай кеңістік толық деп аталады.

def 11.3 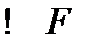- r метрикалы Е метрикалық кеңістігіндегі бейнелеу;

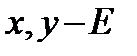кеңістігіндегі нүктелер, ал 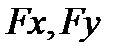-бұл нүктелердің бейнелері болсын. Егер 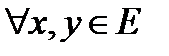екі нүктесі үшін

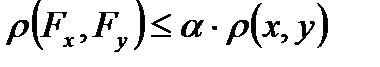(11.5)

теңсіздігі орындалатындай 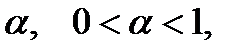саны табылса, онда 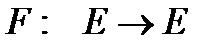бейнелеуі сығылымды бейнелеу деп аталады.

def 11.4 Егер 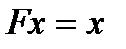болса, онда 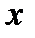нүктесі 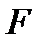бейнелеуінің қозғалмайтын нүктесі деп аталады.

(11.2) жүйеге байланысты қозғалмайтын нүкте-ол сол жүйенің шешімі екені түсінікті.

ТҺ 11.1 (сығылымды бейнелеу принципі). Егер 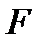-толық метрикалық кеңістікте анықталған сығылымды бейнелеу болса, онда 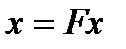теңдігін қанағаттандыратын жалғыз ғана қозғалмайтын 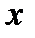нүктесі табылады. Мұндай х⁽⁰⁾ бастапқы мүшесі кезінде 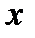-ке жинақты болады. x

Бейнелеудің қозғалмайтын нүктесі мен 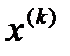жуықтауының арасындағы арақашықтықтың бағалауы келесі формуламен беріледі:

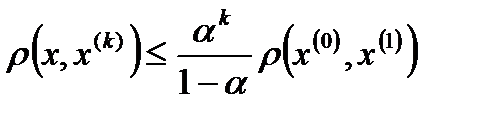(11.6)

Ал бұл теңсіздікте 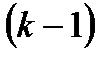-ші жуықтауды нөлінші жуықтау деп қабылдасақ (яғни 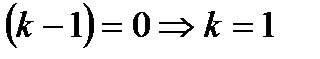), онда тағы бір мынадай маңызды теңсіздікті аламыз:

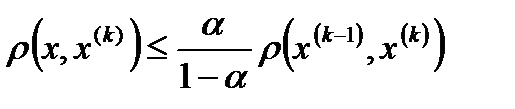(11.7)

Мұнда 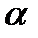- (11.5) сығылу шартындағы көбейткіш.

Сонымен, (11.2) жүйені жай итерация әдісімен шешу үшін (11.3) қатынысымен берілген 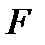бейнелеуі сығылымды екеніне көз жеткізу жеткілікті. Олай болса (11.3) бейнелеуі сығылымды болу шартын қарастырайық. Ал бұл сұрақтың шешімі (11.5) өрнектен көрініп тұрғандай кеңістіктегі метрикаға байланысты. 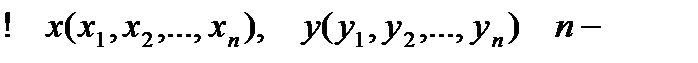өлшемді кеңістіктегі нүктелер болсын. Жай итерация әдісін практикада қолданған кезде САТЖ-н 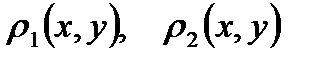немесе 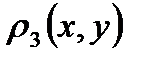метрикаларының біреуімен берілген кеңістікте қарастырған ыңғайлы (1-ші лекция):

;

;

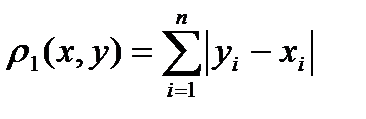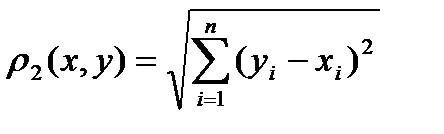р₃(х,у) .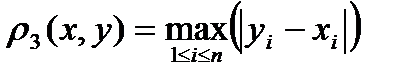

Сонымен, метрикалық кеңістікте (11.3) теңдеулерімен берілген 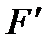бейнелеуі сығылымды болу үшін төмендегі шарттардың біреуінің орындалуы жеткілікті:

а) 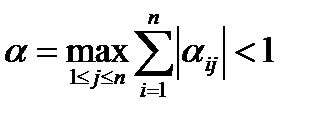; (11.8)

б) ; (11.9)

в) 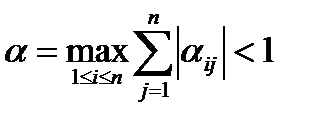. (11.10)

Зейдель әдісі

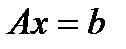(11.1)

теңдеуін, мұндағы 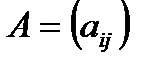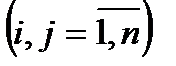- квадратты ерекше емес матрица, келесі түрде жазайық:

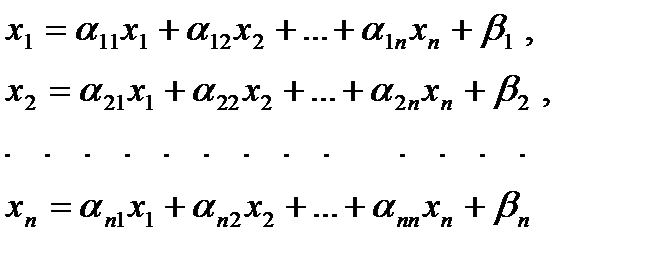(11.2)

немесе қысқаша

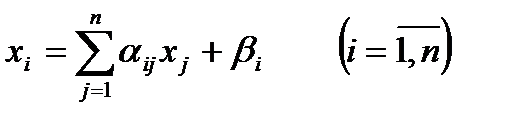
(11.2) жүйенің оң жақтағы 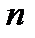-өлшемді векторлық кеңістіктің 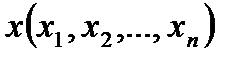нүктесін осы кеңістіктегі нүктесіне түрлендіретін қандайда-бір F бейнесін анықтайды:

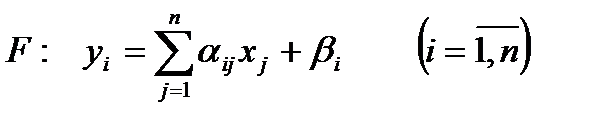(11.3)

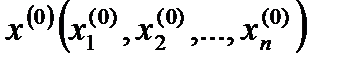бастапқы нүктесін таңдай отырып (11.2) жүйесінің көмегімен 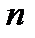-өлшемді кеңістіктегі нүктелердің итерациялық тізбегін құруға болады:

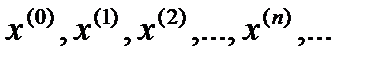(11.4)

Бірінші лекцияда метрика ұғымын ендірген болатынбыз. r матрикасы ендірілген жиын метрикалық кеңістікке айналатыны белгілі.

def 11.1 Егер 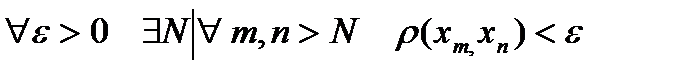теңсіздігі орындалса, онда метриналық кеңістіктің мұндай нүктелер тізбегі фундаменталды деп аталады.

def 11.2 Егер ондағы кезкелген фундаменталды тізбек жинақты болса, онда мұндай кеңістік толық деп аталады.

def 11.3 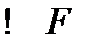- r метрикалы Е метрикалық кеңістігіндегі бейнелеу;

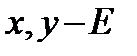кеңістігіндегі нүктелер, ал 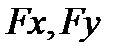-бұл нүктелердің бейнелері болсын. Егер 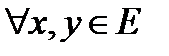екі нүктесі үшін

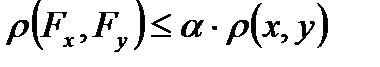(11.5)

теңсіздігі орындалатындай 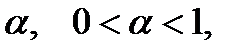саны табылса, онда 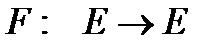бейнелеуі сығылымды бейнелеу деп аталады.

def 11.4 Егер 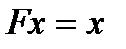болса, онда 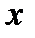нүктесі 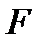бейнелеуінің қозғалмайтын нүктесі деп аталады.

(11.2) жүйеге байланысты қозғалмайтын нүкте-ол сол жүйенің шешімі екені түсінікті.

ТҺ 11.1 (сығылымды бейнелеу принципі). Егер 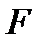-толық метрикалық кеңістікте анықталған сығылымды бейнелеу болса, онда 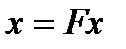теңдігін қанағаттандыратын жалғыз ғана қозғалмайтын 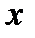нүктесі табылады. Мұндай х⁽⁰⁾ бастапқы мүшесі кезінде 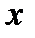-ке жинақты болады. x

Бейнелеудің қозғалмайтын нүктесі мен 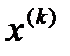жуықтауының арасындағы арақашықтықтың бағалауы келесі формуламен беріледі:

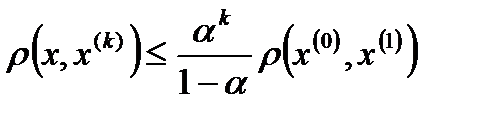(11.6)

Ал бұл теңсіздікте 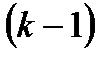-ші жуықтауды нөлінші жуықтау деп қабылдасақ (яғни 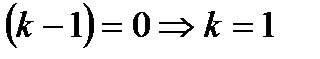), онда тағы бір мынадай маңызды теңсіздікті аламыз:

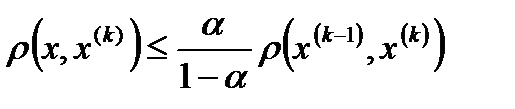(11.7)

Мұнда 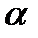- (11.5) сығылу шартындағы көбейткіш.

Сонымен, (11.2) жүйені жай итерация әдісімен шешу үшін (11.3) қатынысымен берілген 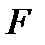бейнелеуі сығылымды екеніне көз жеткізу жеткілікті. Олай болса (11.3) бейнелеуі сығылымды болу шартын қарастырайық. Ал бұл сұрақтың шешімі (11.5) өрнектен көрініп тұрғандай кеңістіктегі метрикаға байланысты. 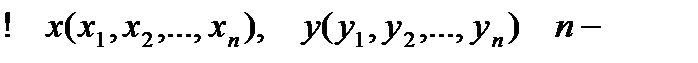өлшемді кеңістіктегі нүктелер болсын. Жай итерация әдісін практикада қолданған кезде САТЖ-н 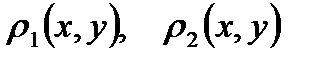немесе 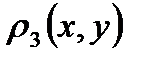метрикаларының біреуімен берілген кеңістікте қарастырған ыңғайлы (1-ші лекция):

;

;

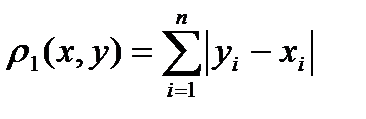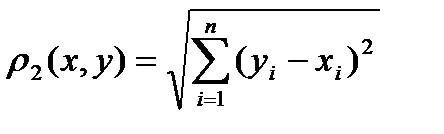р₃(х,у) .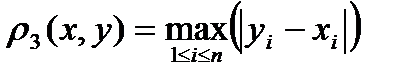

Сонымен, метрикалық кеңістікте (11.3) теңдеулерімен берілген 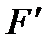бейнелеуі сығылымды болу үшін төмендегі шарттардың біреуінің орындалуы жеткілікті:

а) 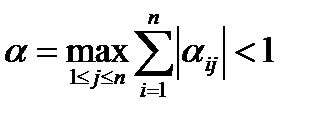; (11.8)

б) ; (11.9)

в) 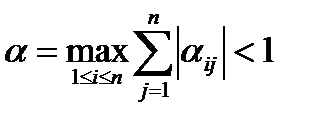. (11.10)

Билет №13

Ортогоналдау әдісі

Берілген жүйе келесідей жазылған болсын.

,

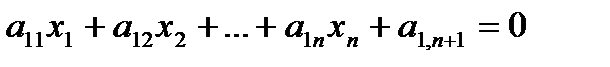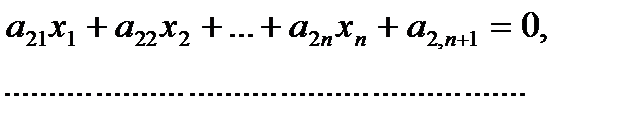(13.1)

,

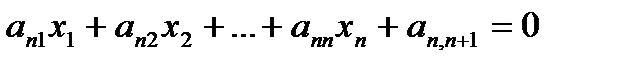әрбір теңдеудің сол жағын

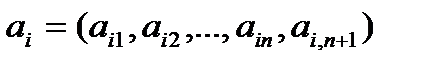
және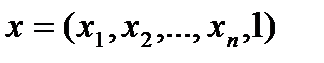

екі вектордың скалярлық көбейтіндісі түрінде қарастыруға болады.

Сонымен (13.1) жүйенің шешімі әрбір 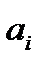векторына ортогоналды болатын векторды табуға келіп тіреледі. 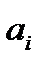векторлар жүйесіне оларға сызықты тәуелді емес. 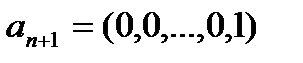векторын қосамыз. 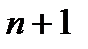- өлшемді векторлық кеңістікте кезкелген 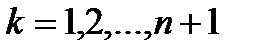кезінде 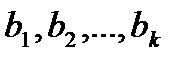векторлары 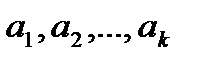қарастырылып отырған векторлары туындайтын 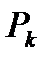ішкі кеңістігінің ортонормалданған базисы болатындай оның 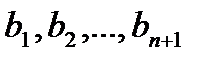ортонормалданған базисын құратын боламыз, ол үшін 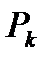ішкі кеңістігінде қандайда бір 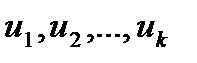ортагоналды базисын құру жеткілікті, ал одан кейін оны нормалдау керек.

Есептеуді төмендегідей алгоритммен жүргіземіз:

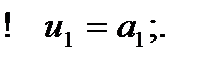
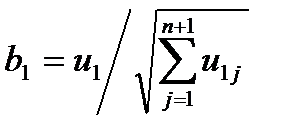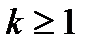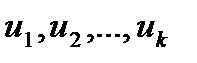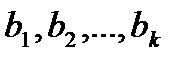. Егер қандайда бір үшін және векторлары құрылып қойсы, онда 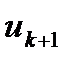векторы

формуласы бойынша бірнеше итерация көмегімен есептеледі. Мұндағы 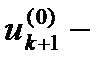бастапқы, ал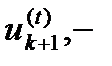 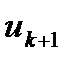векторының кезектегі жуықтауы. 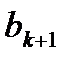векторы 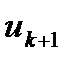векторы бойынша келесі формуламен анықталады:

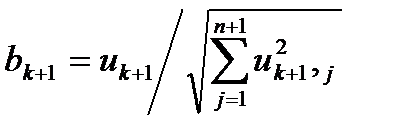
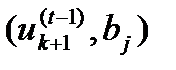бойынша әдетте қабылданғандай векторлардың симметриялық көбейтіндісі белгіленген. (11.1) жүйенің түбірлерінің мәні 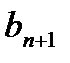векторының координаталармен былайша байланысқан: .

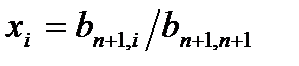Итерациялық қадамдар ортогоналдау процесінің орнықсыздығын мүмкіндігінше болдырмауға жақын, жататынын атап өту керек. Жай жағдайларда келесі формуланы қолдансақ та жеткілікті:

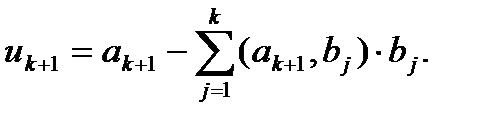
Таблицалық функцияларды интерполяциялау

! Қандайда бір 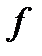функциясының белгілі мәндерінен келесідей кесте құрылысын делік:

			….
			….

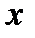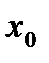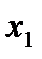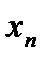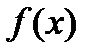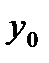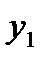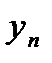кесте 14.1

Интерполяциялау есебі келесі формада қойылады: 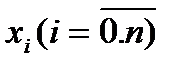нүктелеріндегі мәндері берілген функцияның мәндерімен бірдей болатын дәрежесі 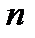-нен жоғары емес 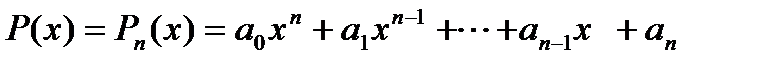(14.1)

көпмүшелігін табу қажет. Мұндай қойылымда интерполяциялау есебі параболалық деп аталады. 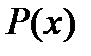көпмүшелігі интерполяциялық көпмүшелік деп, ал 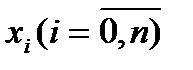нүктелері интерполяция түйіндері деп аталады.

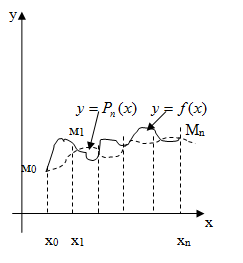
Геометриялық тұрғыдан бұл берілген 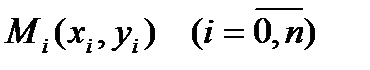нүктелер жүйесі арқылы өтетін 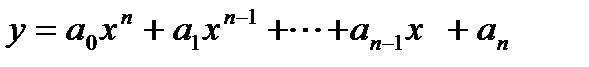түріндегі алгебралық қисықты табу дегенді білдіреді:

Сонымен (14.1) көпмүшелігі

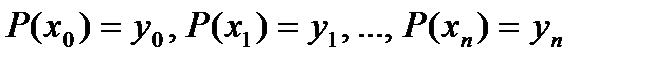(14.2)

шарттарын қанағаттандыруы керек. Сондықтан бұл көпмүшеліктің 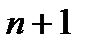белгісіз коэффиценттерін табу үшін осы 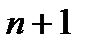(14.2) шартын ескерсек болады:

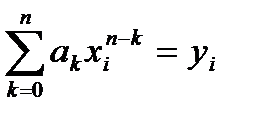
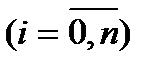(14.3)

Бұл жүйені 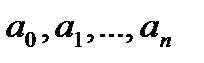белгісіздеріне байланысты шешсек (14.1) полиномының аналитикалық өрнегін алуға болады. (14.3) жүйенің барлық уақытта тек жалғыз ғана шешімі

болады, өйткені оның анықтауышы

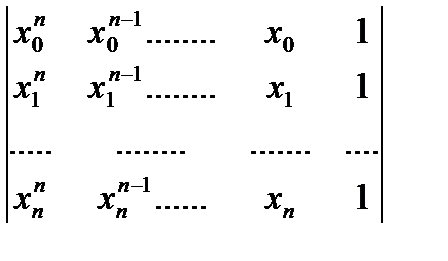
нольден өзгеше (Бұл анықтауыш алгебрада Вандермонд анықтауышы деген атпен белгілі). Сондықтан 14.1-кестемен берілген 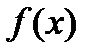функциясы үшін 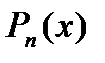интерполяциялық көпмүшелігі барлық уақытта табылады және ол жалғыз. Әдетте практикада интерполяциялық көпмүшелікті құрудың әртүрлі ыңғайлы тәсілдерін көрсетуге болады. Интерполяциялық формулалар аргументтің аралық мәндері үшін 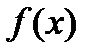функциясының белгісіз мәндерін табуға қолданылады. Бұл кезде интерполяциялау мен экстрополяциялауларды ажырату керек . Интерполяциялау кезінде 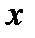нүктесі 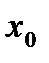мен 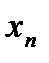-нің арасында жатады, ал экстрополяциялау кезінде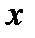 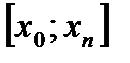аралығының сыртында жатады.

Билет №14