Примеры по расчету электрического поля постоянных токов
Пример 1. Провести расчет электрического поля в плоском конденсаторе с двухслойным диэлектриком. К конденсатору подключено постоянное напряжение U = 4 кВ (рис. 2.5). Площадь обкладок конденсатора s равна 24 см2, толщина слоев – d1 =2 см и d2 =4 см. Удельные проводимости слоев несовершенного диэлектрика равны g1 = 5×10-9 См/м и g2 = 10-8 См/м, относительные значения диэлектрической проницаемости -er1 = 2 и er2 = 5, соответственно.
Пренебрегая краевым эффектом найти распределение напряженности и потенциала в каждом слое. Определить сопротивление утечки конденсатора, поверхностную плотность свободного и связанного зарядов на поверхности раздела двух сред. Рассчитать мощность, выделяющуюся в единице объема диэлектрика.
Решение. Для расчета напряженности электрического поля запишем уравнение для напряжения между пластинами конденсатора, которое по определению имеет вид:
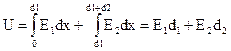
Напряженности поля Е1 и Е2 являются неизвестными величинами, поэтому для их определения необходимо составить еще одно уравнение. Для этого воспользуемся условием (2.5), которое с учетом выражения (2.1) можно представить в следующем виде:
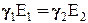 .
.
Решая совместно два последних уравнения, находим значения Е1 и Е2
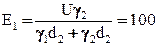 кВ/м;
кВ/м;
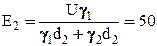 кВ/м.
кВ/м.
Напряжение на каждом слое диэлектрика
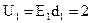 кВ;
кВ; 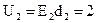 кВ.
кВ.
Используя закон Ома в дифференциальной форме, находим плотность тока в каждом слое
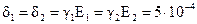 А/м2.
А/м2.
Ток утечки при этом будет равен
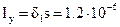 А.
А.
Плотность свободных зарядов на границе раздела диэлектриков определим по формуле
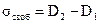 . (2.10)
. (2.10)
Подставляя в выражение (2.10) значения векторов электрического смещения, получим
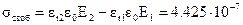 Кл/м2.
Кл/м2.
Плотность связанных зарядов на границе раздела диэлектриков находим через вектор поляризации с помощью формулы
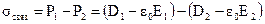 .
.
Подставляя в последнее выражение значения векторов электрического смещения и напряженности электрического поля, получим
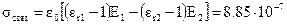 Кл/м2.
Кл/м2.
Активную мощность, выделяющуюся в единице объема каждого диэлектрика, находим с помощью закона Джоуля – Ленца в дифференциальной форме (2.9) PV1 = 50 вт/м3; PV2 = 25 вт/м3.
Активную мощность, выделяющуюся во всем диэлектрике, можно определить с помощью следующего выражения:
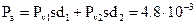 Вт.
Вт.
Сопротивление конденсатора
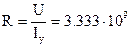 Ом.
Ом.
Отметим, что сопротивление конденсатора можно определить и с помощью метода электростатической аналогии. Для этого в выражение (1.16) для емкости конденсатора с двухслойным диэлектриком необходимо подставить вместо значений диэлектрических проницаемостей удельные значения электрических проводимостей, в результате чего получим значение проводимости G = 3×10-10 См. Сопротивление конденсатора определяется как обратная величина проводимости R = 1/G = 3.333×109 Ом.
Пример 2. К краям плоской алюминиевой пластины (рис. 2.6) подводится постоянное напряжение U = 2 В. Пластина представляет собой половину диска постоянной толщины с концентрически вырезанными круглыми отверстиями. Внутренний радиус диска r1 = 1 см, наружный – r2 = 2 см, толщина пластины h = 1 мм.
 Считая, что линии плотности тока совпадают с полуокружностями и напряженность поля зависит только от радиуса, найти зависимость плотности тока в функции расстояния от центра диска. Рассчитать ток, протекающий по пластине и определить сопротивление пластины.
Считая, что линии плотности тока совпадают с полуокружностями и напряженность поля зависит только от радиуса, найти зависимость плотности тока в функции расстояния от центра диска. Рассчитать ток, протекающий по пластине и определить сопротивление пластины.
Решение. Напряжение между краями пластины определяется с помощью следующего выражения:
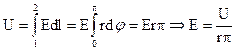 ,
,
здесь r – произвольный радиус (r1 £ r £ r2)
Зная зависимость напряженности поля от радиуса и, используя закон Ома в дифференциальной форме, находим зависимость плотности тока от радиуса
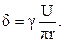
Ток, протекающий по пластине, определяется следующим образом:
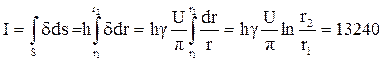 А.
А.
Сопротивление пластины
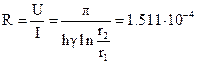 Ом.
Ом.
Пример 3. Заземлитель, который выполнен в виде цилиндрической трубы с наружным радиусом r2 = 2 см, расположен в грунте с удельной проводимостью g3 = 4×10-2 См/м. Длина трубы равна h = 5 м (рис. 2.7).
Определить сопротивление заземлителя.
Решение. Для расчета используем метод зеркальных изображений. В этом случае реальная труба относительно поверхности земли и вся среда считается однородной и имеющей проводимость g = g3. В результате получаем расчетную схему, представленную на рис. 2.8.
Емкость цилиндра, имеющего длину 2h и радиус r2, определяется по формуле (1.21). Заменяя в этой формуле диэлектрическую проницаемость e на удельное электрическое сопротивление земли gз, получаем выражение для проводимости заземлителя (с учетом того, что проводимость заземления для действительного электрода равна половине проводимости, образованной электродом и его зеркальным изображением)
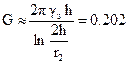 См.
См.
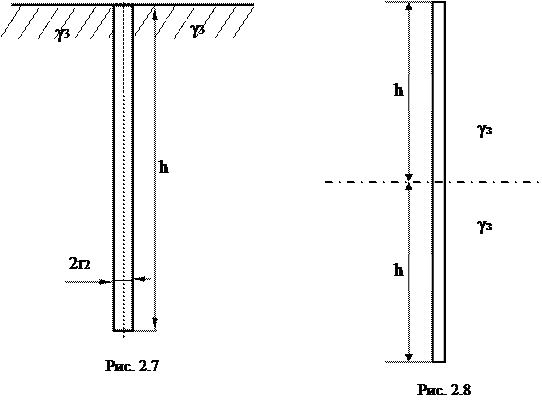
Сопротивление заземлителя R = 1/G = 4.946 Ом.
