Билет 7 Непрерывность функции в точке

Функция 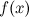называется непрерывной в точке если:

1. функция 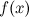определена в точке a и ее окрестности

2. существует конечный предел функции f(x) в точке а .

3. это предел равен значению функции в точке а ,т .е .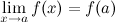

При нахождении предела функции y=f(x) которая является непрерывной, можно переходить к пределу под знаком функции, то есть.

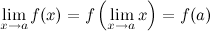
Билет 8 Классификация точек разрыва функции.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел (см. выше) , то функция называется непрерывной справа

Если односторонний предел (см. выше) 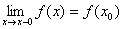, то функция называется непрерывной слева.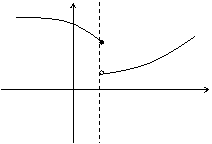

Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Теоре́ма Больца́но — Коши́ о промежуточных значениях непрерывной функции это утверждение, что если непрерывная функция принимает два значение, то она принимает и любое значение между ними.

Формулировка

Пусть дана непрерывная функция на отрезке 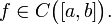Пусть также 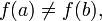и без ограничения общности предположим, что 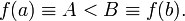Тогда для любого 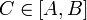существует 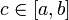такое, что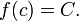

Определение производной.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

11.

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

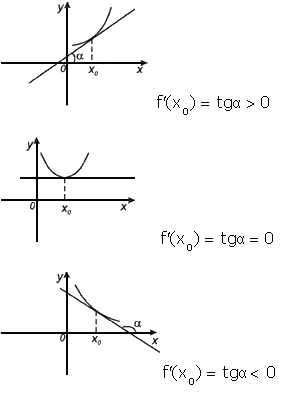
Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

· Пусть функция 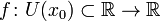определена в некоторой окрестности точки 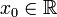, и дифференцируема в ней: 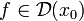. Касательной прямой к графику функции 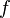в точке 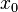называется график линейной функции, задаваемой уравнением

.

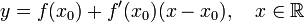· Если функция 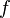имеет в точке 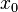бесконечную производную 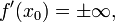то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением

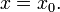
Прямо из определения следует, что график касательной прямой проходит через точку 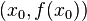. Угол 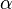между касательной к кривой и осью Ох удовлетворяет уравнению

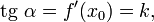
где 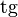обозначает тангенс, а 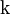— коэффициент наклона касательной. Производная в точке 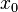равна угловому коэффициенту касательной к графику функции 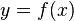в этой точке.

Пусть 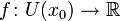и 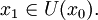Тогда прямая линия, проходящая через точк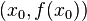и и 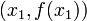задаётся уравнением

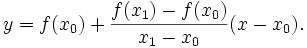
Эта прямая проходит через точку 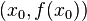для любого 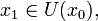и её угол наклона 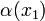удовлетворяет уравнению

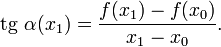
В силу существования производной функции 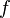в точке 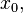переходя к пределу при 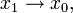получаем, что существует предел

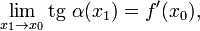
а в силу непрерывности арктангенса и предельный угол

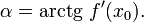
Прямая, проходящая через точку 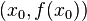и имеющая предельный угол наклона, удовлетворяющий 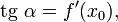задаётся уравнением касательной:

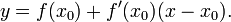
Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.

1. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

2. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

3. Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания.