ЧАСТЬ 2: ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ К ИССЛЕДОВАНИЮ ФУНКЦИЙ. Интервалы выпуклости и точки перегиба

Лекция 10

Интервалы выпуклости и точки перегиба

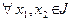Определение 19. Пусть J – некоторый интервал на действительной прямой. Говорят, что функция выпукла вниз (соответственно, строго выпукла вниз) на J, если , таких, что 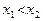, выполняется неравенство:

(соотв., ).

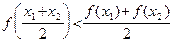(32)

Если неравенства в (32) заменить на противоположные, то получаем определение выпуклой вверх (соотв., строго выпуклой вверх) функции.

€

Теорема 22 (критерий выпуклости). Пусть функция дважды дифференцируема на открытом интервале 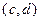. Эта функция выпукла вниз (соотв., выпукла вверх) тогда и только тогда, когда (соотв., ).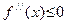

Доказательство. Докажем теорему для функций, выпуклых вниз.

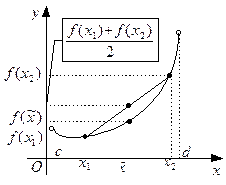Предположим, что и пусть 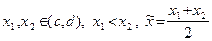. Имеем:

.
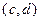Так как функция дифференцируема на , то по лемме 3 она непрерывна на 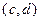. Поэтому на отрезке выполнены все условия теоремы Лагранжа (см. теорему 15), из которой следует существование точки 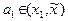, такой, что . Аналогично рассуждая, получаем: 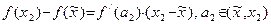. Учитывая, что , имеем:

.
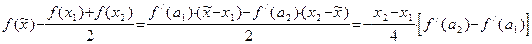Из условий теоремы и из леммы 3 так же, как и ранее, следует, что функция на отрезке 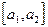удовлетворяет условиям теоремы Лагранжа. Поэтому существует точка 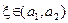, такая, что . Итак, мы получаем равенство:

.

Так как по условию 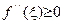, то правая часть этого равенства неположительна, следовательно , что в соответствии с определением 19 доказывает выпуклость вниз функции .

Перед рассмотрением обратного утверждения заметим, что если в начале полученного доказательства предположить, что 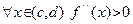, то проведенное рассуждение даст строгую выпуклость вниз функции .

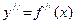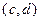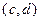Обратное утверждение теоремы докажем лишь при условии, что функция непрерывна на (без этого предположения доказательство значительно сложнее). Итак, пусть выпукла вниз на , но существует точка 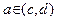, такая, что 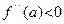. Из непрерывности в точке a функции 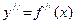следует, что существует такая d-окрестность этой точки, что 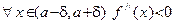(докажите это от противного!). Поэтому из замечания, сделанного после доказательства первой части теоремы и примененного к выпуклым вверх функциям, получаем, что функция строго выпукла вверх на интервале . Полученное противоречие завершает доказательство теоремы.

€

Пример 31. Рассмотрим функцию 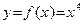. Так как 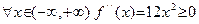, то из теоремы 22 следует, что эта функция выпукла вниз на всей действительной прямой. Легко видеть, что на самом деле 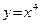строго выпукла вниз на 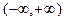(докажите это!). При этом, однако, . €

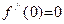Пример 31 показывает, что в полном объеме аналог теоремы 22 не может быть сформулирован для строго выпуклых функций. Однако справедлива следующая теорема, доказательство которой дословно повторяет первую часть доказательства теоремы 22.

Теорема 23. Пусть функция дважды дифференцируема на открытом интервале 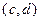. Если 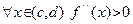, (соотв., 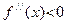), то строго выпукла вниз (соотв., строго выпукла вверх) на . ›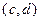

Для запоминания теорем 22 и 23 существует мнемоническое "правило дождя":

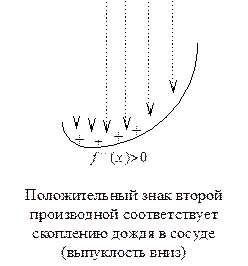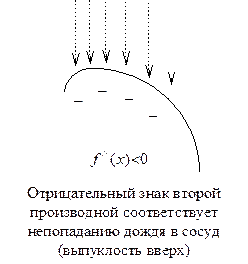Следующая теорема, доказательство которой подобно доказательству теоремы 22 и поэтому нами опускается, дает характеризацию интервалов выпуклости в терминах касательных.

Теорема 24. Пусть функция дважды дифференцируема на открытом интервале 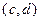. Она выпукла вниз (соотв., выпукла вверх) на этом интервале тогда и только тогда, когда график функции лежит выше (соотв, ниже) касательной к этому графику, проведенной в точке .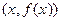

€

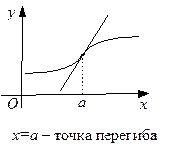Определение 20. Говорят, что точка 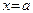является точкой перегиба графика функции , если эта функция определена в некоторой окрестности точки a, имеет касательную в этой точке и при переходе через эту точку меняет выпуклость вниз на выпуклость вверх или наоборот.

€

Теорема 25 (необходимое условие точки перегиба). Если функция дважды дифференцируема в окрестности точки 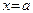и эта точка является точкой перегиба графика данной функции, то .

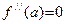Доказательство. Предположим для определенности, что слева от точки a лежит интервал выпуклости вниз функции , а справа – интервал выпуклости вверх. Используя теорему 22, заключаем, что 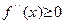слева от a и 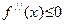справа от a. Применяя к функции достаточный признак экстремума (см. теорему 18), заключаем, что в точке 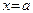эта функция имеет локальный максимум. По теореме Ферма (теорема 12) .

€

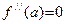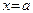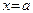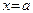Теорема 26 (достаточные условия точки перегиба). Пусть в точке функция имеет касательную, а в окрестности этой точки (за исключением, быть может, самой точки) – дважды дифференцируема. Если при переходе через точку вторая производная меняет знак, то – точка перегиба графика функции .

Доказательство немедленно следует из теоремы 22 и определения 20.

€

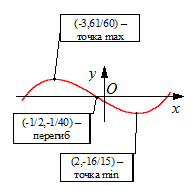Пример 32 (продолжение примеров 21 и 26). Найдем вторую производную исследуемой функции: 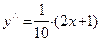. Так как , то это единственная точка, "подозрительная" на перегиб. Заполняем таблицу для второй производной, наносим на график точки перегиба и уточняем поведение графика в смысле выпуклости:

x		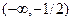–1/2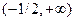
	–		+
y		–1/40
		перегиб

Пример 33 (продолжение примеров 22 и 27). Имеем:

.

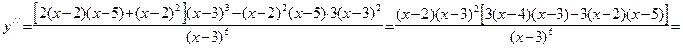
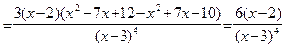x			(2,3)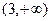
	–		+	+
y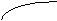
		перегиб

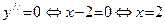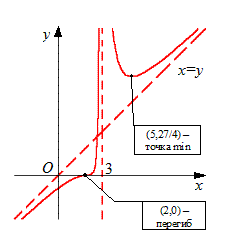
Так как , то 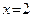– единственная точка, подозрительная на перегиб. Строим таблицу и уточняем график. Заметим, что в таблицу для второй производной не следует вносить стационарные точки, не являющиеся подозрительными на перегиб (в данном случае речь идет о точке ).

Пример 34 (продолжение примеров 23 и 28). Имеем:

.

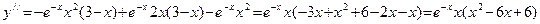Далее: 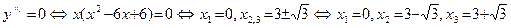. Получили три точки, подозрительные на перегиб.

x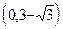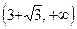
	–		+		–		+
y
		пер		пер		пер

€

Читателю предлагается самостоятельно исследовать на выпуклость функции из примеров 24 (см. также пример 29) и 25 (см. также пример 30).