Сызықтық жүйелердің орнықтылығы

Қарапайым жағдайдан бастайық – күй кеңістігіндегі қоздырылмаған ашық жүйеден. Басқару жоқ болған кезде жүйе ашық деп аталады

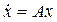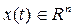, , (5.5)

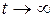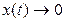мұндағы A – n×n-өлшемді, t уақытына тәуелсіз матрица, егер кез келген x(0) үшін кезде болса орнықты деп аталады.

Теорема 5.1. (5.5) жүйесінің орнықтылығы үшін А матрицасының барлық s_i меншікті мәндері сол жақ жарты жазықтықта жатқаны қажетті және жеткілікті:

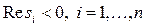. (5.6)

Бұл жағдайда кез келген 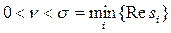үшін сондай тұрақты С = C(A,ν), бар болады, келесі теңсіздікті қанағаттандыратын

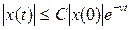(5.7)

Атап өтейік, (5.6) шартын қанағаттандыратын А матрицасы осыдан әрі қарай гурвицтік немесе орнықты деп аталады. Осыған сәйкес, теріс нақты бөлікті меншікті мәндерді де орнықты деп атайтын боламыз.

Егер А орнықты болса, онда 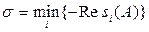шамасы (матрицаның немесе сәйкес жүйенің) орнықтылық дәрежесі деп аталады, яғни ол орнықты матрицаның меншікті мәнінен жорамал оське дейінгі минималды қашықтық.

Дәлелдеу.Қажеттілігі. (5.6) шарты орындалмайды деп ұйғарайық, яғни кейбір меншікті мәндері, мысалы s₁ сондай

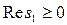
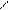
болатын А матрицасы табылады. Егер s₁ нақты болса, онда 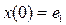аламыз, мұнда 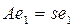, e₁ - нақты вектор және 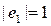. Онда мұндай бастапқы шартты шешімнің түрі 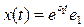болады және сондықтан 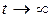болғанда x(t) 0. Егер s₁ – комплексті сан 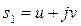болса, онда 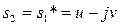түйіндес меншікті мән табылады, және оған қоса, егер 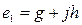- меншікті вектор болса, s₁ меншікті мәніне 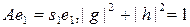жауапты, ал 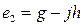- меншікті векторы үшін, s₂ меншікті мәніне 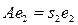жауапты. Бұл жағдайда 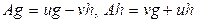. 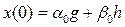аламыз, мұнда 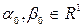, онда x(t) сол екі өлшемдік төменгі кеңістікте қалады: 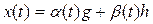, мұнда 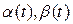келесі дифференциалдық теңдеулермен сипатталады

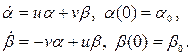
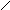
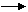
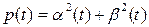белгілеуі арқылы , 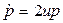оңай аламыз, яғни 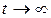және u > 0 болғанда p(t) 0.

Жеткіліктілігін дәлелдеу (матрицалық экспоненттерді бағалау). А матрицасы диогональдық түрге келтірілетін (мысалы, оның барлық меншікті мәндері әртүрлі нақты мән қабылдайды) болсын деп ұйғарайық, яғни сондай азғындалмаған Т матрицасы бар болады, келесі теңдіктер орындалатын

.

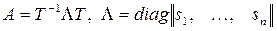Бұл жағдайда аламыз

.

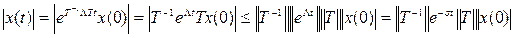Осы орнықты матрица үшін баға (5.7) дәлелдейді. Бұл жағдайда 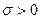, сондықтан v = σ деп алуға болады, ал С тұрақтысы айқын түрде жазылады

.

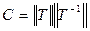Матрицалық тұлғада алынған нәтижені матрицалық экспонентаның бағалануы түрінде жазуға болады

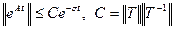. (5.8)

А матрицасы диогональдық түрге келтірілетін жағдай өте қарапайым, себебі 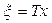түріндегі айнымалыларды алмастыруды жүргізсек, жүйені келесі түрге келтіруге болады

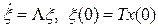
немесе басқаша айтқанда, 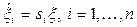, яғни (5.5) шешімдері

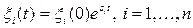
болатын тәуелсіз n теңдеуге ыдырайды.

Егер 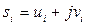және барлық 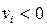болса, онда барлық s_i үшін 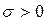және 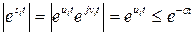болады, сондықтан .

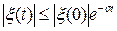Жалпы жағдайда А матрицасы ұқсастық түрлендірумен диогональдық емес, блоктық жордано тұлғасына келтіріледі

,

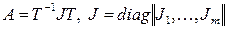және жүйе J_i блоктарына сәйкес төмендегі тәуелсіз m жүйеге жіктеледі. Бір J_i жордано блогы үшін келесі l × l өлшемдік матрицаны аламыз

.

.

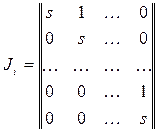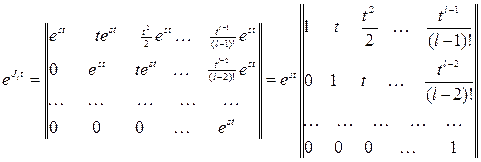Сондықтан, егер 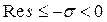болса, онда l – 1 дәрежелі сондай R(t) палиномы табылады, кез келге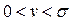н үшін 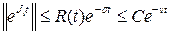теңсіздігі орындалатын; мұнда 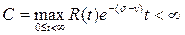. 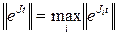шамасын 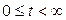болғанда ескере отырып, (5.7) бағалауына келуге болады.

Айта кету керек, (5.6) шарттарын қанағаттандыратын (5.5) жүйесі орнықты болатындығына қарапайым талдаудың да көмегімен көз жеткізуге болады.

Теңдеу (5.5) үшін сипаттамалық теңдеуді келесі түрде жазуымызға болады:

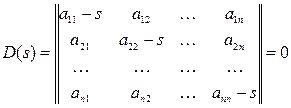. (5.9)

Сипаттамалық теңдеу (5.9) ізделінетін s мәнін табуға болады, яғни s₁, s₂, ... s_n – олар сипаттамалық теңдеудің түбірлері болады.

(5.5) теңдеуінің шешімдерін алуымызға болады

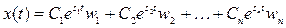. (5.10)

Басқаша айтқанда, шешімнің уақыттан тәуелділігі экспоненциалды функциямен сипатталады. Сипаттамалық теңдеулерінің түбірлері немесе А матрицасының меншікті мәндері уақытқа тәуелсіз w₁, w₂, …, w_т меншікті векторларды табуға мүмкіндік береді, ал олар өсу немесе кему жылдамдықтарын береді. С_i – алғашқы шарттары 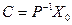арқылы анықталады. Атап өту қажет, жалпы жағдайда s₁, s₂, ... s_n шамалары комплексті мәнді қабылдайды, ал w₁, w₂, …, w_т векторлары x(t) айнымалысының векторлық сипаттамасын ескереді.

Сонымен, орнықтылық проблемасы шешіледі, егер s₁, s₂, ... s_n меншікті мәндері табылатын болса, ал w₁, w₂, …, w_т меншікті векторлардың бұл жағдайда қандай да қасиеттерінің болуына байланыссыз. Шынымен, x уақытқа тәуелді (5.10) қатынасымен анықталатын болғандықтан, жазамыз

.

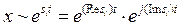Мұнда Res_i және Ims_i – сәйкесінше s_i комплексті шаманың нақты және жорамал бөлігі. Осыдан алымыз, Res_i < 0 болса, x мәні экспоненциалды уақыт бойынша кемиді. Бұл өшу тербелістерімен модуляцияланады, егер Ims_i нольге айналмаса. Осыдан аламыз, қоздырылмаған (стандартты) шешімді (күйді) аламыз, 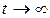болғанда x = 0 шегіне жететін. Бұл сызықтандырылған жүйенің асимптотика-лық орнықтылығын білдіреді. Екінші жағынан, егер Res_i > 0 болса, онда қоздырылған x қозғалысыэкспоненциалды өсетін болады, оған сәйкес x = 0 стандартты шешімі орнықсыз болады.