Бесконечно большая функция (б.б.ф.)
Функция y=f(x) называется бесконечно большой величиной при x→ x0 , если для любого числа M>0 существует число 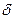 =
= 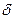 (M)>0, такое что для всех x, удовлетворяющих условию |x- x0|<
(M)>0, такое что для всех x, удовлетворяющих условию |x- x0|< 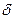 , будет верно неравенство |f(x)|>M. Записывается
, будет верно неравенство |f(x)|>M. Записывается 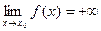 или
или 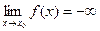 .
.
Свойства бесконечно больших функций:
- Произведение бесконечно большой величины на функцию, предел которой отличается от 0, есть величина бесконечно большая;
- Сумма б.б.в. и ограниченной функции есть величина бесконечно большая;
- Частное от деления (б.б.в.) на функцию имеющую предел есть (б.б.в.)
Бесконечно малые функции.
Функция y=f(x) называется бесконечно малой при x→ x0 , если 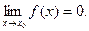
По определению предела функции это означает: для любого числа 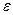 >0 найдется число
>0 найдется число 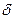 >0 такое, что для всех x удовлетворяющих |x-x0|<
>0 такое, что для всех x удовлетворяющих |x-x0|< 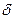 будет верно |f(x)| <
будет верно |f(x)| < 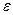 . Бесконечно малые функции часто называют бесконечно малыми величинами и обозначаются обычно греческими буквами α,β и т.д.
. Бесконечно малые функции часто называют бесконечно малыми величинами и обозначаются обычно греческими буквами α,β и т.д.
Примеры: y=x2 при x→0, y=x-2 при x→ 2
1. Свойства бесконечно малой функции:
1. Алгебраическая сумма б.м.функций есть тоже б.м.функция.
Доказательство:
Пусть α(x) и β(x) две б.м.ф. при x→x0. Это значит, что 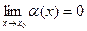 , т.е. для любого
, т.е. для любого 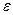 >0, а значит, и
>0, а значит, и 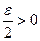 найдется число
найдется число 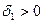 такое, что для всех x, удовлетворяющих
такое, что для всех x, удовлетворяющих
| x-x0|< 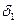 выполняется |
выполняется | 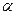 (x)| <
(x)| < 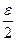 . Тоже будет и для
. Тоже будет и для 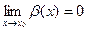 при | x-x0|<
при | x-x0|< 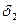 и
и 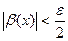 . Пусть
. Пусть 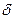 - наименьшее из чисел
- наименьшее из чисел 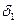 и
и 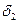 тогда для всех x, удовлетворяющих
тогда для всех x, удовлетворяющих
|x-x0|< 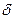 , выполняются оба неравенства и, складывая их, получим:
, выполняются оба неравенства и, складывая их, получим: 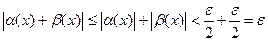 .
.
Это означает, что 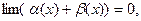 т.е.
т.е. 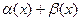 – б.м.в. при x →x0.
– б.м.в. при x →x0.
Остальные свойства б.м.ф. приведем без доказательств.
2. Произведение двух б.м.ф. друг на друга есть функция бесконечно малая.
Следствие: произведение б.м.ф. на число есть б.м.ф.
3. Частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
4. Если функция f(x) имеет предел равный A, то ее можно представить как сумму числа A и бесконечно малой функции α(x), т.е. если 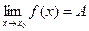 , то
, то 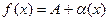 .
.
Доказательство: пусть 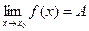 , следовательно, для любого
, следовательно, для любого 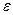 >0 найдется
>0 найдется 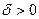 такое, что при
такое, что при 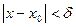 выполняется
выполняется 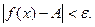 т.е.
т.е. 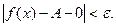 Это означает, что функция f(x)-A имеет предел равный нулю, т.е. является б.м.в., которую обозначим через
Это означает, что функция f(x)-A имеет предел равный нулю, т.е. является б.м.в., которую обозначим через 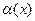 ,т.е.
,т.е. 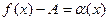 , отсюда
, отсюда 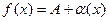 . Верна и обратная теорема, если
. Верна и обратная теорема, если 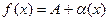 , то
, то 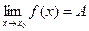 .
.
5) Основные теоремы о пределах.
1. Предел суммы(разность) двух функций равен сумме (разности) их пределов.
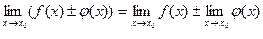
Доказательство: Пусть 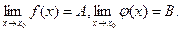 Тогда по теореме 4 можно записать
Тогда по теореме 4 можно записать
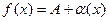 и
и 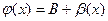 , т.е.
, т.е. 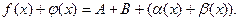 Здесь α(x)+β(x)- б.м.ф. как сумма б.м.ф. По обратной теореме 4 можно записать
Здесь α(x)+β(x)- б.м.ф. как сумма б.м.ф. По обратной теореме 4 можно записать
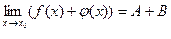 , т.е.
, т.е. 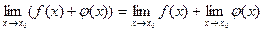
При разности доказательство аналогично.
Следствие 1. Функция может иметь только один предел при x→ x0 . Пусть 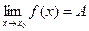 и
и  Вычитая, получим
Вычитая, получим 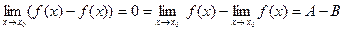 , отсюда A-B=0, т.е. A=B
, отсюда A-B=0, т.е. A=B
2. Предел произведения двух функций равен произведению их пределов.
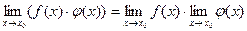
Доказательство: т.к. 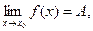 а
а 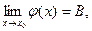 то
то 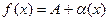 и
и 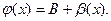 Следовательно:
Следовательно: 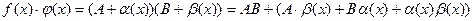 .
.
Выражение в скобках есть б.м.ф. Поэтому 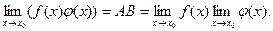
Теорема справедлива для любого конечного числа функций.
Следствие. Постоянный множитель можно выносить за знак предела 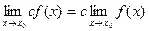 .
.
Доказательство: 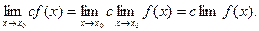
Следствие. Предел степени с натуральным показателем равен той же степени предела
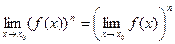
Доказательство: 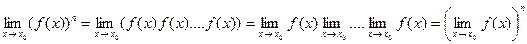
3.Предел дроби равен пределу числителя, деленному на предел знаменателя если предел знаменателя ≠0.
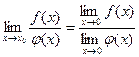
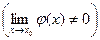
Доказательство: 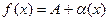 и
и 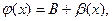 а
а 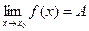 и
и 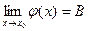
Тогда 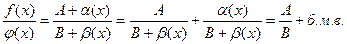
Тогда 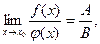 т.е.
т.е.