Расчёт приведённых моментов инерции.

Инертные свойства машин и механизмов характеризуют приведённой массой, либо приведённым моментом инерции, в зависимости от того, линейным или угловым является перемещение звена приведения.

Приведённый момент инерции механизма может быть приведён к главному валу машины, для чего его величину умножают на квадрат передаточной функции от звена приведения к указанному валу.

Приведённый к главному валу машины момент инерции её маховых масс вычисляют как сумму произведений масс и моментов инерции её звеньев, а также приведённых масс; либо приведённых моментов инерции её механизмов, на квадраты передаточных функций в движении приводимых звеньев и звеньев приведения относительно вала машины, принятого

за главный.

Главным приведённым моментом компрессора будет момент, приведённый к валу кривошипа ОА.

Приведённый момент ротора приведённого электродвигателя:

I_p.пр = I_p×U_пер² = = 0,27 кг×м²

Приведённый момент зубчатой передачи:

I_{пер. пр.} = (I_пл + I_Z5)×U_5-6+ I_Z6 ,

где I_пл – приведенный к валу водило момент инерции планетарного механизма, а величину I_пл вычисляем:

I_пл = I_н + I_Z1× U_пл² + k×(m_Z2+ m_Z3 (V₀₁/ω_H)²+ I_Z2+ I_Z3 ×(ω₂/ω_H)²); где k – число сателлитов

Передаточная функция :

V₀₁/ω_H = l_H = (d₁+d₂)/2 = (0,045+0,1125)/2 = 0,079 м

ω₂/ω_H = (Z₁+Z₂)/Z₂ = (d₁+d₂)/d₂

ω₂/ω_H = (0,045+0,1125)/0,1125= 1,4; а U_пл= 7

Остальные данные берем из таблицы 6.1.

Получаем:

I_пл = 0,016+ 1,4×10^-2×49+3[(0,387+2,23)×0,079²+(6,1·10^-4+0,02)×1,4²]= 8,6922 кг×м²

При этом:

I_{пер. пр} = (8,6922+3,8·10^-4) ·1,4 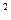+1,5·10^-3 = 17,04кг×м²

Приведенный момент инерции несущего механизма:

I_нес.пр. = I₀₁+ I₀₃(ω₃/ω₁)²+( m₄(Vs₄/ω₃)²+ I_s4(ω₄/ω₃)²+m₅(V_D/ω₃)²)*( ω₃/ω₁)²

где передаточная функция в движении ползуна 5 относительно кривошипа BC может быть вычислена как:

;где ;

; ; ;

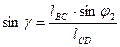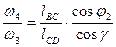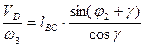
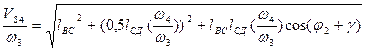
,где углы 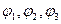-соответственно показаны на рис.6.1:

РИС. 6.1

Полученные результаты расчетов заносим в таблицу 6.2 и 6.3: таблица 6.2

положение	φ1	lba,м	φ3	φ2	ώ3/ώ1	ώ4/ώ3	γ	Vs4/ώ3	VD /ώ3
		0,0425			1,00387	-0,5		0,1125
		0,0572			0,77522	-0,3491		0,09904	0,03699
		0,062			0,7353	0,1091		0,07289	0,08155
		0,0546			0,80457	0,4051		0,0943	0,06799
		0,0425			1,00387	0,5		0,1125
		0,0331			1,32718	0,4051	-19	0,09431	-0,06799
		0,0305			1,47083	0,27815	-26	0,07924	-0,08324
		0,0296			1,53241	0,19368	-28	0,07438	-0,08412
		0,0296			1,53241	-0,19368	-28	0,08634	-0,05684

таблица 6.3

Положение кривошипа А0	Значение обобщенной координаты	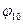Работа сил	Приращение критической энергии	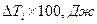Момент инерции, приведенный к валу кривошипа,
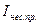					0,27	17,04	0,064391
				-3,62	0,27	17,04	0,041567
				-12,84	0,27	17,04	0,064632
				-19,88	0,27	17,04	0,07069
				-12	0,27	17,04	0,064391
				-8,96	0,27	17,04	0,19073
				-7,74	0,27	17,04	0,274428
				-7,12	0,27	17,04	0,293837
				-4,96	0,27	17,04	0,192244
					0,27	17,04	0,064391

φ⁰₁₀ – угол поворота кривошипа ОА от своего нулевого положения, соответствующего одному из крайних положений ползуна.

В таблице определено:

∆Т_i=А_дi-Ас_i

На листе 1 строим диаграмму энергомасс – зависимость ∆Т_i от ∆I_прi. С помощью этой диаграммы находим момент инерции постоянной составляющей маховых масс(I^*_пр), при которой частота вращения приводного электродвигателя за цикл установившегося движения изменяется соответственно допустимому коэффициенту δ изменения средней скорости хода. Такое ограничение необходимо для предохранения приводного электродвигателя от перегрева, для повышения общего к.п.д. работы компрессора за счет снижения получаемого тепла обмотками электродвигателя. Принимаем:

δ=0,01

Средняя угловая скорость вала кривошипа ОА:

ω_ср= π·n_кр/30 = π·145/30 = 15,18 с^-1

Углы наклона касательных к диаграмме энергомасс определяем по формулам:

tgψ_max=μ_I·(1+ δ)·ω_ср²/(2· μ_T);

tgψ_min=μ_I·(1-δ)· ω_ср²/(2· μ_T); где

μ_I=0,0033 кг×м²/мм;

μ_T=10 Дж/мм – масштабы приведенного момента инерции и энергии, выбранные для диаграммы энергомасс.

После подстановки чисел получаем:

tgψ_max=0,0033·(1+0,01)·15,18²/(2·10)=0,038401558;

tgψ_min=0,0033·(1-0,01)·15,18²/(2·10)=0,037641132;

Откуда:

ψ_max=2,2⁰ ψ_min=2,16⁰

Проведя касательные к диаграмме под указанными углами к оси ∆I_прi, находим отрезки О₁К и О₁L(в мм), которые используем для определения координат начала О системы Т- I_пр - зависимости полной кинетической энергии движущихся звеньев механизма от их приведенного момента инерции (О₁К = -0,7мм; О₁L=-199,6мм).

Уравнения касательных:

y=x tgψ_max+ О₁К;

y=x tgψ_min+ О₁L;

Решаем совместно вычитанием второго уравнения из первого:

мм

После чего подстановка в первое уравнение дает:

y=-284491·0,0384-0,7=-10929,7мм

Постоянная составляющая момента инерции насоса:

I_пр^*=x×μ_I=284491·0.0033=932,82 кг×м²

T₀=y× μ_T=10929,7*10=109297 Дж

Чтобы перейти от системы координат ∆Т-∆I к системе Т-I_пр, вычислим:

Т=Т₀+∆Т_max= 109297+1988=111285 =111,285 кВт·сек=111,285/3600=0,031 кВт·ч

Что соответствует подводимой из сети энергии

Т^*=Т/η_дв=0,031/0,98=0,032 кВт·ч.

Максимальный маховый момент определим по следующей формуле

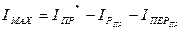
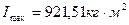
Задаваясь радиусом маховика r=0.5 м примем его массу m_мах=921,51/0,5²=3686,04 кг.

Переносим маховик на более быстроходный вал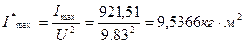

Пересчитываем массу маховика m_мах=9,5366/0,5²=38,15 кг

Определяем ориентировочную массу звеньев станка.

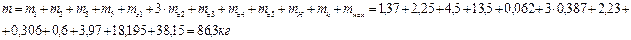
а с учетом массы электродвигателя, соединительных валов и деталей (принимаем м_соед=0,1·м), станины (принимаем м_стан=1,2·м), ориентировочная масса станка оказывается приблизительно равной

М=м+0,1·м+1,2·м=2,3·м=198,48 кг.

6. ИСЛЕДОВАНИЕ СХЕМЫ ПОРШНЕВОГО КОМПРЕССОРА.

При разработке технического предложения параллельно синтезу схемы ведут анализ, в процессе которого уточняют значения принимаемых величин, исследуют параметры используемых механизмов, проводят оценку эксплуатационных характеристик машины и т.д.