Гіпотеза про рівність двох ймовірностей біноміальних розподілів
Нехай в двох генеральних сукупностях проводяться незалежні випробування: в результаті кожного випробування подія А може появитися в першій сукупності з невідомою ймовірністю 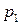 , а в другій – з невідомою ймовірністю
, а в другій – з невідомою ймовірністю 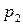 . За вибірками, взятими з першої та другої сукупності, знайдені відповідні частоти:
. За вибірками, взятими з першої та другої сукупності, знайдені відповідні частоти: 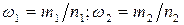 , де
, де 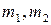 – числа появи події А, а
– числа появи події А, а 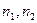 - кількості випробувань. За оцінки невідомих ймовірностей
- кількості випробувань. За оцінки невідомих ймовірностей 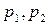 приймають відповідно частоти
приймають відповідно частоти 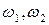 .
.
Потрібно для заданого рівня значущості 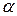 перевірити нульову гіпотезу
перевірити нульову гіпотезу 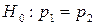 . Для її перевірки використовується статистика:
. Для її перевірки використовується статистика:
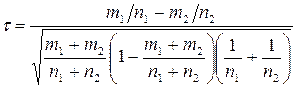 . (4.32)
. (4.32)
При альтернативних гіпотезах: 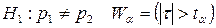 , , де
, , де 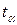 –розв’язок рівняння
–розв’язок рівняння 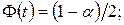 при
при 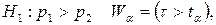
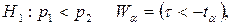 В останніх двох випадках
В останніх двох випадках 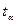 - розв’язок рівняння
- розв’язок рівняння  .
.
Приклад 4.19. При аналізі результатів семестрових екзаменів з деякого предмету на першому та другому курсах отримано, що зі 110 студентів першого курсу 16, а зі 106 студентів другого курсу 17 отримали негативну оцінку. Для рівня значущості 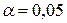 перевірити нульову гіпотезу
перевірити нульову гіпотезу 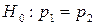 про те: що однаковий процент студентів першого та другого курсів отримали негативну оцінку при альтернативній гіпотезі
про те: що однаковий процент студентів першого та другого курсів отримали негативну оцінку при альтернативній гіпотезі 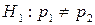 .
.
Розв’язок. За формулою (4.32) обчислюємо оцінку 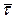
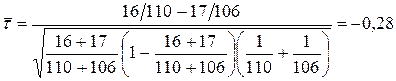 .
.
За таблицею 2 у додатку отримуємо, що 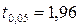 . Оскільки
. Оскільки 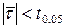 , то нема підстав відкинути нульову гіпотезу.
, то нема підстав відкинути нульову гіпотезу.
Контрольні запитання і задачі
1. Що називається статистичною гіпотезою?
2. Що таке альтернативна гіпотеза і як вона вибирається?
3. Які ви знаєте види гіпотез?
4. Яка гіпотеза називається простою, а яка складною?
5. Що називається критерієм узгодження?
6. Яка область називається критичною, а яка областю прийняття гіпотези?
7. Що таке критична точка?
8. Які ви знаєте види критичних областей ? Дайте їх визначення.
9. Який зміст помилок першого і другого родів?
10. Яку величину називають надійністю критерію, а яку – потужністю?
11. Яку статистику використовують у двовибірковому критерії узгодження М.В. Смірнова і який вона має розподіл?
12. Яку статистику вибирають у критерії 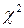 і який вона має розподіл?
і який вона має розподіл?
13. Наведіть загальну схему перевірки гіпотези про розподіл за допомогою критерію 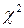 .
.
14. Для яких випадкових величин використовують критерій Колмогорова?
15. Наведіть приклади основних параметричних гіпотез і дайте їх коротку характеристику.
16. При експертній оцінці вагомості фактору “Економічна ситуація на підприємстві і в галузі”, який впливає на внутрішньогосподарський ризик, групою 20 експертів отримано наступні результати: 30, 10, 0, 20, 10, 13, 15, 2, 10, 15, 16, 2, 5, 10, 5, 10, 0, 5, 0, 8. Перевірити вибірку на однорідність для рівня значущості 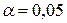 .
.
17. При експертній оцінці вагомості факторів, що впливають на внутрішньогосподарський ризик, двома експертами отримано наступні результати:
| І | |||||||||||||
| ІІ |
Для рівня значущості 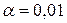 перевірити нульову гіпотезу
перевірити нульову гіпотезу 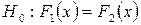 про однорідність оцінок обох експертів при альтернативній гіпотезі
про однорідність оцінок обох експертів при альтернативній гіпотезі 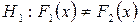 .
.
18. При експертній оцінці вагомості факторів «Комплексний і незвичний характер операцій та їх складність» та «Капітальні вкладення», які впливають на внутрішньогосподарський ризик, групою з 20 експертів отримано наступні результати:
 | ||||||||||||||||||||
 |
Для рівня значущості 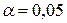 перевірити нульову гіпотезу
перевірити нульову гіпотезу 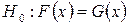 про співпадання розподілів оцінок обох факторів.
про співпадання розподілів оцінок обох факторів.
19. В результаті проведення двох вибірок об’ємами 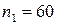 і
і 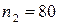 при дослідженні деякої ознаки в генеральній сукупності отримано такі середні значення
при дослідженні деякої ознаки в генеральній сукупності отримано такі середні значення 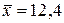 і
і 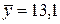 . Зробивши припущення про те, що дана ознака в генеральній сукупності нормально розподілена, необхідно перевірити гіпотезу
. Зробивши припущення про те, що дана ознака в генеральній сукупності нормально розподілена, необхідно перевірити гіпотезу 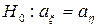 при альтернативній гіпотезі
при альтернативній гіпотезі 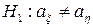 , якщо
, якщо 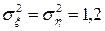 .
.
20. В умовах прикладу 17, допустивши, що оцінки експертів розподілені нормально, для рівня значущості 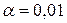 перевірити нульові гіпотези:
перевірити нульові гіпотези:
а) 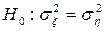 при
при 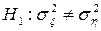 ; б)
; б) 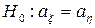 при
при 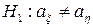 .
.
21. При експертній оцінці вагомості фактору “Використання кредитів банку”, що впливає на внутрішньогосподарський ризик, отримані наступні результати: 8,1,0,5,10,4,6,5,5,6,2,10,2,10,2,10,10,5,6,3. Допустивши, що дані оцінки розподілені нормально, для рівня значущості 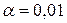 перевірити нульову гіпотезу
перевірити нульову гіпотезу 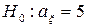 , при альтернативній гіпотезі
, при альтернативній гіпотезі  .
.
22. Роботу групи експертів при оцінюванні вагомості впливу факторів на різні види ризику, вважають узгодженою, якщо дисперсія результатів оцінювання не повинна перевищує 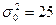 .З результатів оцінювання взяли вибірку 10,30,25,20,20,25,15,15,13,9,5,5,25,15,30,10,15,10,25,20. Допустивши, що результати оцінювання розподілені нормально, для рівня значущості
.З результатів оцінювання взяли вибірку 10,30,25,20,20,25,15,15,13,9,5,5,25,15,30,10,15,10,25,20. Допустивши, що результати оцінювання розподілені нормально, для рівня значущості 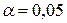 перевірити нульову гіпотезу
перевірити нульову гіпотезу 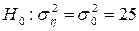 при альтернативній гіпотезі
при альтернативній гіпотезі 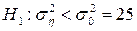 .
.
23. Трьома експертами за 100 бальною шкалою проведена оцінка вагомості всіх факторів, що впливають на внутрішньогосподарський ризик і отримані наступні результати.
| І | |||||||||||||
| ІІ | |||||||||||||
| ІІІ |
Чи можна для рівня значущості 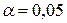 стверджувати про узгодженість оцінок експертів. (Припускається, що оцінки експертів розподілені нормально).
стверджувати про узгодженість оцінок експертів. (Припускається, що оцінки експертів розподілені нормально).
24. Для аналізу результатів вступних випробувань з мови ( хі) та математики (уі) взята вибірка об’ємом n = 45 і отриманий наступний емпіричний розподіл:
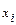 | |||||||||||||||||||
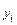 |
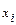 | ||||||||||||||||||
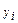 |
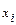 | ||||||||||||||||||||
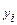 |
Для рівня значущості 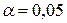 перевірити чи значимо відрізняються результати вступних випробувань з мови і математики між собою, за умови, що вони розподілені нормально.
перевірити чи значимо відрізняються результати вступних випробувань з мови і математики між собою, за умови, що вони розподілені нормально.
25. При аналізі результатів семестрового екзамену з деякого предмету отримано, що зі 106 студентів в першому семестрі 22 отримали негативну оцінку. Для рівня значущості 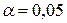 перевірити нульову гіпотезу
перевірити нульову гіпотезу 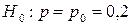 при альтернативній гіпотезі Н1:
при альтернативній гіпотезі Н1: 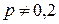 .
.
26. При аналізі результатів семестрових екзаменів з деякого предмету зі 106 студентів в першому семестрі 22 отримали негативну оцінку, а в другому 16. При рівні значущості 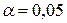 перевірити нульову гіпотезу
перевірити нульову гіпотезу 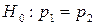 при альтернативній
при альтернативній 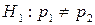 .
.
27. Дані про розподіл підприємств легкої промисловості в області за розподілом продуктивності праці (в % до попереднього року) представляються вибіркою.
Для рівня значущості 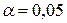 перевірити гіпотезу про нормальність розподілу генеральної сукупності.
перевірити гіпотезу про нормальність розподілу генеральної сукупності.
28. Реєструвався час прибуття студентів в читальний зал бібліотеки з 11 до 18 год. і отримали наступні результати:
 | [11-12) | [12-13) | [13-14) | [14-15) | [15-16) | [16-17) | [17-18] |
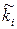 |
Для рівня значущості 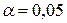 перевірити гіпотезу про те що час прибуття студентів в читальний зал розподілений рівномірно.
перевірити гіпотезу про те що час прибуття студентів в читальний зал розподілений рівномірно.
29. В результаті реєстрації часу прибуття 800 відвідувачів виставки, одержано наступний емпіричний розподіл:
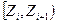 | 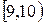 | 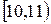 | 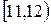 | 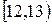 | 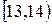 | 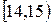 | 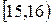 | 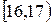 |
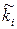 |
де 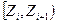 – інтервали часу, а kі – кількість відвідувачів, які прийшли на виставку протягом даного інтервалу часу. Для рівня значущості
– інтервали часу, а kі – кількість відвідувачів, які прийшли на виставку протягом даного інтервалу часу. Для рівня значущості 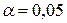 перевірити гіпотезу про те, що час прибуття відвідувачів на виставку розподілений за показниковим законом.
перевірити гіпотезу про те, що час прибуття відвідувачів на виставку розподілений за показниковим законом.
30. При перевірці 200 контейнерів зі скляними виробами встановлено, що число 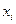 пошкоджених виробів має розподіл
пошкоджених виробів має розподіл
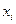 | ||||||
 |
Для рівня значущості 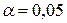 перевірити гіпотезу про те, що випадкова величина
перевірити гіпотезу про те, що випадкова величина 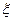 =(число пошкоджених виробів) має розподіл Пуассона.
=(число пошкоджених виробів) має розподіл Пуассона.
Застосування ППП
Розглянемо роботу відповідних процедур в ППП STATISTICA.
Для проведення аналізу необхідно виконати такі операції
Analysis
Other statistics
Customize list
Вибрати зі списку:
Basic statistics
Replace
Switch to …
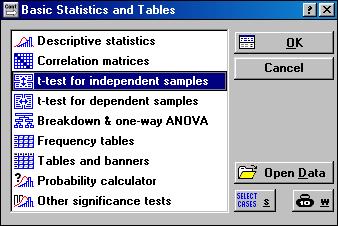
1. У підменю, що з’явилось, вибрати тип аналізу: t-test for independent samples (тест для незалежних вибірок).
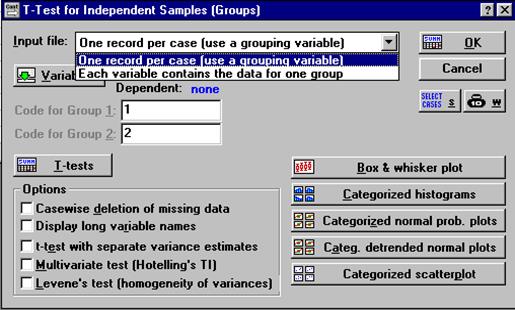
2. Послідовно заповнити у новому вікні такі поля:
Input file (вхідний файл), для чого стрілочкою у правій частині рядка розкрийте список і виберіть у ньому опцію:
Each variable contains the data for one group (кожна змінна містить дані для однієї з порівнюваних груп). У цьому разі дані про дві вибірки організовані у вигляді однієї змінної.
3. Вибрати T-test та натиснути на його клавішу. У вікні з’являться результати розрахунків.
Те саме можна виконати для залежних вибірок: у підменю, що з’явилось, вибрати тип аналізу:  .
.
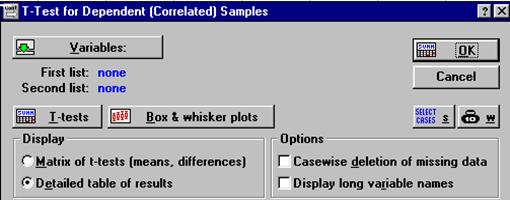
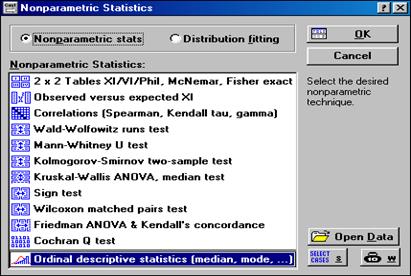
Модуль Непараметрична статистика містить набір таких непараметричних статистик:
· Pearson Chi-square – критерій узгодження Пірсона;
· Maximum-Likelihood Chi-square –критерій максимальної правдоподібності;
· Fisher exact test–точний тест Фішера;
· McNemar Chi-square (A/D, B/C).критерій Мак-Немара;
· Coefficient of contingency –коефіцієнт контингенції.
Для того, щоб обчислити коефіцієнти рангової кореляції у модулі непараметричної статистики вибираємо 
Після вибору модуля з’явиться меню розрахунку рангових кореляцій:
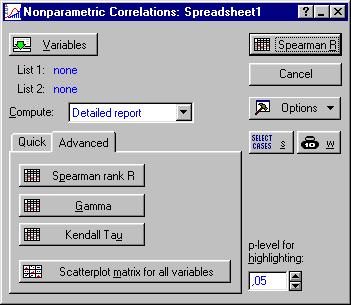
· Spearman R –коефіцієнт рангової кореляції Спірмена;
· Kendall tau –коефіцієнт рангової кореляції Кендалла;
· Gamma –гамма -коефіцієнт.
Для того, щоб здійснити перевірку гіпотез в Microsoft Excelпотрібно зайти в Сервис ØНастройки
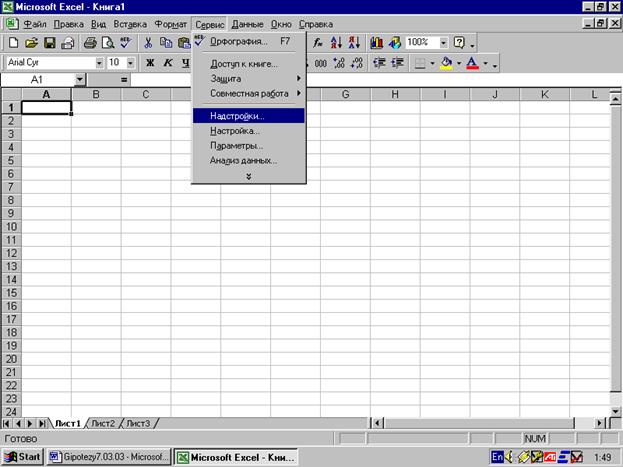
потім вибираємо Пакет анализа
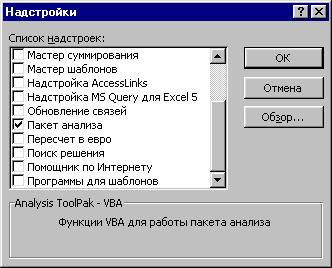
Натискаємо ОК.