Расчет сложной электрической цепи методом узловых потенциалов.

ИССЛЕДОВАНИЕ СЛОЖНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА

Цель работы - получение опытных и расчетных данных для построения потенциальной диаграммы и проверки основных законов электрических цепей.

УИР: исследование электрической цепи с более сложной схемой.

ОБЩИЕ СВЕДЕНИЯ

Перед выполнением работы прорабатывают теоретический мате­риал из учебника [l] или [2].

Потенциальная диаграмма показывает распределение потенциалов вдоль участка или контура электрической цепи в функции от величин сопротивлений. Построенная для замкнутого контура, потенциальная диаграмма является графическим изображением уравнения второго закона Кирхгофа. Знание величин потенциалов в электрических цепях в условиях эксплуатации представляет не только теоретический интерес, но и практическую необходимость. Например, при составлении схем реальных электроэнергетических и электротехнических устройств о точки зрения получения наименьших по отношению к сумме потенциалов и правильного выбора изоляции отдельных элементов схемы.

Для построения потенциальной диаграммы необходимо знать (кроме сопротивлений участков) потенциалы точек электрической цепи или токи в ветвях (их величины и направления), по которым можно вычислить потенциалы.

Перед определением потенциалов произвольно задают направление обхода рассматриваемого участка или контура и обозначают буквами или цифрами точки цепи, для которых будут определяться потенциалы. Выбирают базисную точку, относительно которой производится измерение или расчет потенциалов остальных точек. При этом надо помнить:

· ток в пассивном элементе протекает от точки с большим потенциалом к точке с меньшим;

· если на участке цепи между двумя точками имеются источники ЭДС с направлением действия, совпадающим с направлением тока, то потенциал в последующей по направлению обхода точке повышается, и наоборот.

Например, потенциалы точек в ветви сложной электрической цепи, приведенной на рис. 1, а, при известном направлении тока вычисляются следующим образом (принимая φ_А =0):

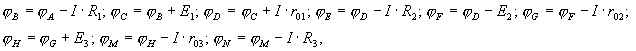
где r₀₁, r₀₂, r₀₃ - внутренние сопротивления источников ЭДС.

При построении потенциальной диаграммы точки на координатной плоскости, соответствующие величинам потенциалов, соединяют прямыми линиями, как показано на рис. 1, б, где приведена потенциальная диаграмма для ветви (рис. 1, а). Тангенс угла наклона прямых к оси абсцисс определяет в масштабе величину тока. Потенциальная диаграмма позволяет определить падения напряжения (разность потенциалов) на любом из участков. Кроме того, по потенциальной диаграмме можно судить о целесообразности выбора базисной точки о точки зрения величии потенциалов. Потенциал базисной точки обычно принимается равным нулю, что в условиях эксплуатация соответствует ее заземлению. Изменение базисной точки влечет за собой изменение величин потенциалов остальных точек цепи, не вызывая при этой изменения токов и напряжений в схеме.

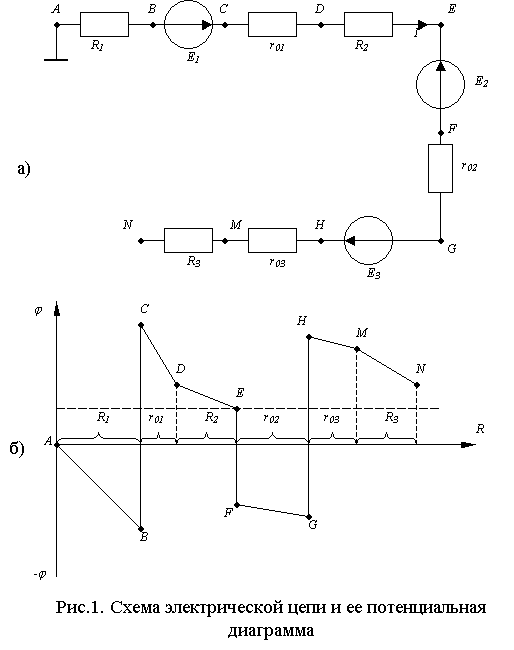
В условиях эксплуатации, если схема подлежит заземлению, точка заземления выбирается так, чтобы потенциалы остальных то­чек были наименьшими. На потенциальной диаграмме изменению базисной точки соответствует параллельный перенос горизонтальной оси так, чтобы ось проходила через эту точку. Например, если на схеме (рис. 1, а) принять в качестве базисной точку Е, то ось абсцисс будет расположена так, как показано на рис, 1, б, пунктиром. Имея потенциальную диаграмму легко определить, какую точку схемы рационально выбрать в качестве базисной и рекомендовать для заземления.

В данной работе потенциалы точек определяют эксперименталь­но и проверяют расчетом. Расчет токов (по которым затем вычисля­ют потенциалы точек) производят методом узловых потенциалов. Для расчета токов необходимо знать величины ЭДС, их внутренние сопротивления и сопротивления участков цепи, которые опреде­ляются по результатам измерений (см. приложение).

В работе также проверяют баланс мощностей.

В любой электрической цепи энергия, отдаваемая источниками, равна энергии, потребляемой приемниками. Сопротивления элементов электрических: цепей, т.е. приемников и внутренние сопротивления источников ЭДС, потребляют энергию W и преобразуют ее в тепло. Энергия, потребляемая приемником с сопротивлением R в течение времени Dt.

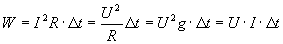
Скорость изменения энергии во времени представляет мощность

В цепях постоянного тока при U = const, I=const,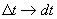

мощность 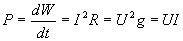, (Вт).

Аналогично мощность источников ЭДС , Вт.

Если направление действия ЭДС и тока совпадают, то P_E – положительна, и источник отдает энергию, если не совпадают, то P_E - отрицательна и источник работает в режиме потребителя.

Для сложной электрической цепи уравнение баланса мощностей записывается следующим образом;

(*)

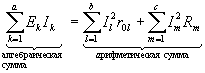Используя опытные данные, необходимо проверить баланс мощностей, составив уравнение согласно (*). Кроме того, убедиться в том, что выполняются первый и второй законы Кирхгофа:

· алгебраическая сумма токов в узле электрической цепи равна нулю;

· алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжений на участках контура.

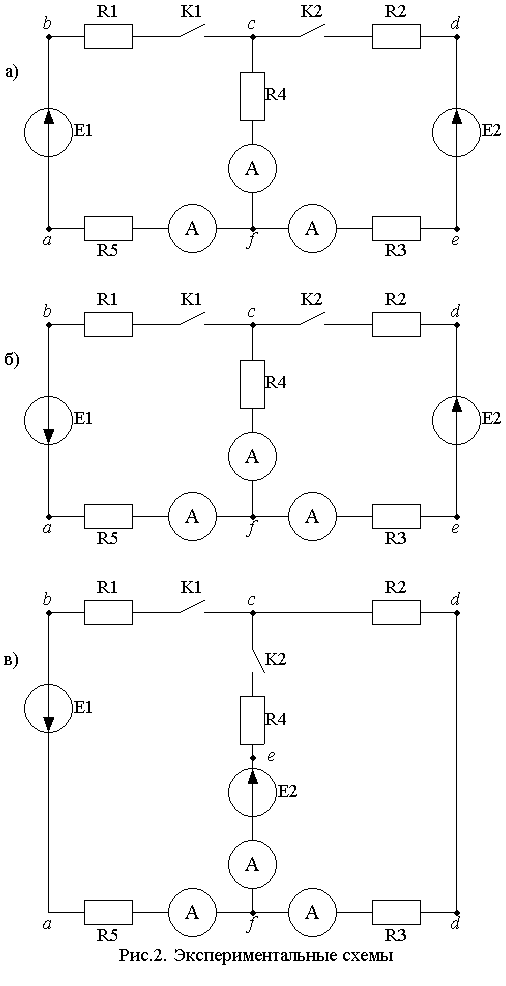
Схемы исследуемых в работе электрических цепей представлены на рис.2, а, б, в. Для УИР – схема рис.2, г.

2. ПРОГРАММА РАБОТЫ

1) Начертить схему исследуемой цепи, указанную преподавате­лем (рис.2, а ,б ,в) и открыть файл, в котором задана модель схемы.

2) Измерить ЭДС источников, токи, напряжения на участках и потенциалы всех точек исследуемой цепи (базисная точка указывается преподавателем).

3) По опытным данным, полученным в п. 2, определить внутрен­ние сопротивления источников ЭДС и сопротивления участков электрической цепи.

4) Составить уравнения I и II законов Кирхгофа и баланса мощностей. Проверить их, подставив численные значения из п.2.

5) Произвести расчет токов методом узловых потенциалов, а также расчет потенциалов точек исследуемой цепи и сопоставить результаты расчета с опытными данными.

6) Построить потенциальную диаграмму для контура, указан­ного преподавателем. Из диаграммы определить точки, имеющие наибольший φ_max потенциал.

7) Ответить на вопрос: какую точку схемы следует брать в качестве базисной, чтобы получить, наименьшие величины потенциалов остальных точек данного контура?

УИР: для схемы (рис.2, г) выполнить п.1-3, 6 программы и исследовать: как влияет выбор базисной точки (заземления схемы) на величины потенциалов, формы таблиц наблюдений составить самим.

ВЫПОЛНЕНИЕ РАБОТЫ

П.1 программы. Собрать одну из схем, представленных на рис. 2.

п.2 программы. Не замыкая рубильников К1 и К2 измерить ЭДС источников, присоединяя вольтметр V к зажимам источников и следя за тем, чтобы зажим вольтметра, имеющий знак «+», был подсоединен к положительному зажиму источника.

Замкнуть рубильники K1 и K2.(Подобрать сопротивление резисторов так, чтобы амперметры показывали токи 0 – 2 А). Измерить токи и напряжения на отдельных участках цепи с помощью микродисплеев I1, I2, I3 . При записи токов в табл.1 знак тока можно не учитывать. Измерение напряжения между двумя точками цепи (например U_аb ) производится следующим образом: зажим «+» вольтметра подключается к точке, соответствующей первой букве индекса (т.е.- "а"), а "-" - ко второй точке (т.е. «b»). Показания вольтметра записываются с учетом знака. Результаты измерений занести в табл. 1. Для схемы рис.2, в индексы напряжений несколько изменятся.

Измерить потенциалы точек тем же вольтметром. Для этого отрицательный зажим вольтметра присоединяют к базисной точке, указанной преподавателем (потенциал её принимают равным нулю), а положительный зажим – к точке, потен­циал которой измеряют. Показания вольтметра записываются с учетом знака. Результаты измерений занести в табл. 2. После каждого переключения вольтметра схему нужно запускать на моделирование

Таблица 1

Наблюдаются

Вычисляются

E1, В

Е2, В

I1, А

I2, А

I3, А

Uab, В

Ubc, В

Ucd, В

Ude, В

Uef, В

Ufa, В

Ufc, В

I1, А

I2, А

I3, А

.

Таблица 2

Наблюдается	Вычисляется
φа, В	jb, В	φc, В	φd, В	φe, В	φf, В	φа, В	φb, В	φc, В	φd, В	φe, В	φf, В

п. 3 программы - Внутренние сопротивления источников опреде­ляются по формуле

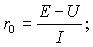
ЭДС источников и напряжения (U) на зажимах источника при подключенной нагрузке берутся из п. 2 программы. Сопротивления резисторов вычисляются по закону Ома

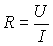
где U - падение напряжения на резисторе;

I - ток, протекающий по резистору.

Результаты измерений записывают в табл. 3.

Таблица 3

r01, Ом	r02, Ом	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом

п.4 и 5 программы выполняются в соответствием с указания­ми, приведенными в разделе "Общие сведения". Уравнение второго закона Кирхгофа составляют для внешнего контура.

п.6 программы. Потенциальная диаграмма отроится в прямо­угольной системе координат. Начало координат должно соответство­вать потенциалу базисной точки, т.е. нулю. По оси абсцисс в мас­штабе откладывают последовательно одну за другой в направлении обхода контура величины сопротивлений участков цепи, а по оси ординат – потенциалы точек цепи. Нанесенные на координатной плос­кости точки, соответствующие величинам потенциалов, соединяют прямыми линиями.

СОДЕРЖАНИЕ ОТЧЕТА

1) Программа работы.

2 Схема и модель исследуемой цепи.

3) Таблицы наблюдений, формулы и примеры вычислений.

4) Потенциальная диаграмма, уравнение баланса мощности и опытная проверка 1-го и 2-го законов Кирхгофа.

5) Краткие выводы.

5. ЛИТЕРАТУРА

1 )Нейман Л. Р., Демирчян К. С. Теоретичес­кие основы электротехники. Т. I. Л.: Энергоиздат, ,1981.

2) Б е с с о н о в Л. А. Теоретические основы электротех­ники. М.: Высшая школа, 1979.

ПРИЛОЖЕНИЕ

Расчет сложной электрической цепи методом узловых потенциалов.

В качестве примера рассмотрим схему рис.5.

1) Записываются основные характеристики конфигурации цепи - количество ветвей "р" и узлов "q".

р = 5; q = 3.

2) В денной схеме 5 неизвестных токов: I₁, I₂, I₃, I₄, I₅

Потенциал узла "f" примем равным нулю.

Согласно теории по методу узловых потенциалов записывается (q-1) уравнений, т.е. два.

Для узла "c" запишем:

и для узла "d":

3. Решая эту cиcтему 2-х уравнений относительно потенциалов φ_с и φ_d определяем их.

4. Произвольно задав направление токов в ветвях электричес­кой цели на рис.5 записываем выражения токов через потенциа­лы узлов на основании закона Ома для участка цепи, содержащей ЭДС.

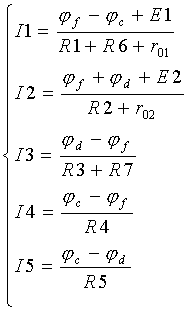(1)

Подставляя виденные ранее φ_с и φ_d в (1), определяем токи в ветвях рассматриваемой электрической цепи (их величину и направление).