Включення і рівність нечітких множин
Означення 2.23. Нехай задані нечіткі підмножини 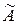 ,
, 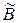 множини
множини 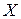 . Ступінь включення
. Ступінь включення  , нечіткої множини
, нечіткої множини 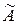 в нечітку множину
в нечітку множину 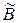 визначається по формулі
визначається по формулі  , де
, де 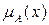 ,
,  ступені належності елемента
ступені належності елемента 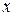 до множин
до множин 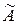 і
і 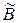 .
.
Якщо  , то
, то 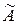 нечітко включається в множину
нечітко включається в множину 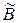 й позначається
й позначається  . Якщо
. Якщо 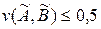 , то
, то 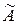 нечітко не включається в множину
нечітко не включається в множину 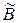 й позначається
й позначається 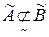 . Це поняття є узагальненням поняття включення для чітких множин. Дійсно, нехай
. Це поняття є узагальненням поняття включення для чітких множин. Дійсно, нехай  и
и  - чіткі множини й
- чіткі множини й 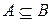 , звідси випливає
, звідси випливає 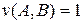 . Якщо ж
. Якщо ж 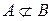 , то
, то 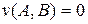 .
.
Приклад 2.20. Нехай задано множину 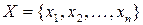 , і в неї дві нечіткі множини
, і в неї дві нечіткі множини 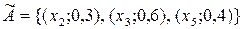 і
і 
 , тоді:
, тоді:
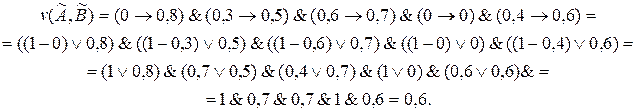
Аналогічно можна обчислити 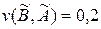 , звідки випливає
, звідки випливає 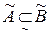 , але
, але 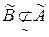 .
.
Означення 2.24. Ступінь рівності двох нечітких підмножин 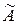 ,
, 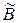 множини
множини 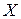 визначається як
визначається як 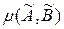 , де
, де 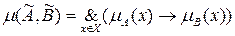 .
.
Якщо 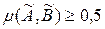 , то множини нечітко рівні
, то множини нечітко рівні 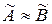 . Якщо
. Якщо 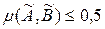 , то множини нечітко не рівні
, то множини нечітко не рівні 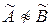 . Якщо
. Якщо 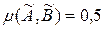 , то множини взаємно індиферентні
, то множини взаємно індиферентні 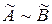 .
.
Поняття нечіткої рівності й нерівності, індиферентності є узагальненням понять рівності й нерівності для чітких множин. Дійсно, нехай  й
й  – чіткі множини, тоді у випадку
– чіткі множини, тоді у випадку 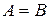 ,
, 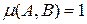 , якщо ж
, якщо ж 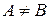 и
и 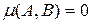 .
.
Приклад 2.21. Нехай задано множину  і в неї дві нечіткі множини
і в неї дві нечіткі множини  і
і 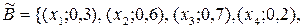
 знайдемо ступінь рівності множин
знайдемо ступінь рівності множин 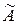 і
і 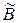 :
:
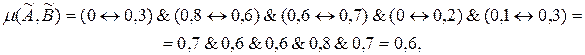
звідки випливає 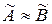 .
.
Означення 2.25. Нечітка множина 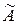 дорівнює нечіткій множині
дорівнює нечіткій множині 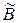 .
.
 , якщо
, якщо  .
.
Неважко помітити, якщо виконується рівність множин  , то ці множини є й нечітко рівними
, то ці множини є й нечітко рівними 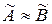 .
.
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що таке множина? Наведіть приклади різних множин.
2. Як можна визначити множину?
3. Скільки існує способів подання множин? Охарактеризуйте їх.
4. Що таке скінчена та нескінченна множини?
5. До якої з цих множин належить порожня множина?
6. Для чого використовується порожня множина?
7. Сформулюйте парадокс Рассела.
8. Дайте означення об’єднання множин.
9. Дайте означення перерізу множин.
10. Дайте означення різниці множин.
11. Дайте означення диз’юнктивної суми (алгебраїчної різниці) множин.
12. Що таке кола Ейлера?
13. Що таке універсум?
14. Дайте означення операції абсолютного доповнення
15. Що таке підмножина? Наведіть приклади.
16. Чи завжди будь-яка множина містить порожню множину? Аргументуйте відповідь.
17. Чим відрізняється за значенням строге включення Ì від включення Í. Аргументуйте відповідь.
18. Чим відрізняється поняття включення множин (Ì або Í) від поняття належності (Î).
19. Як розрізнюють елементи множини та її підмножини? Відповідь ілюструйте прикладами.
20. Що таке множина-степінь? Які використовуються при цьому позначення?
21. Чи може множина входити до складу своїх елементів?
22. Що таке розбиття із позиції теорії множин? Наведіть приклади різних класів.
23. Сформулюйте комутативні закони алгебри множин.
24. Сформулюйте асоціативні закони алгебри множин.
25. Сформулюйте дистрибутивні закони алгебри множин.
26. Сформулюйте закони самопоглинання алгебри множин.
27. Сформулюйте закони поглинання алгебри множин.
28. Сформулюйте теореми де Моргана алгебри множин.
29. Як узагальнюються операції над множинами.
30. Що таке простір і функція належності?
31. Що таке розпливчаста (нечітка) множина? Наведіть приклади таких множин.
32. Як визначається універсальна множина в теорій нечітких множин?
33. Що таке нечітка множина?
34. Що таке носій нечіткої множини?
35. Що таке висота нечіткої множини?
36. Що таке точка переходу нечіткої множини?
37. Що таке лінгвістична змінна?
38. Що таке базова терм-множина?
39. Що таке атомарний терм?
40. що таке підтерм? Наведіть приклади різних підтермів?
