Статистический анализ результатов эксперимента
Планирование эксперимента исходит из статистического характера зависимостей, поэтому полученные уравнения подвергаются тщательному статистическому анализу с целью извлечь из результатов эксперимента максимум информации и убедиться в достоверности полученной зависимости и ее точности. Как уже отмечалось ранее, каждый эксперимент несет в себе какую-то погрешность, для повышения надежности результатов производятся для каждой строки таблицы планирования повторения опытов m* раз.
Построчные (выборочные) дисперсии подсчитываются по формуле
(1.14)
где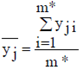 
– средний отклик по m* опытам в точке с номером j.
Дисперсия воспроизводимости отклика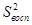 
есть среднеарифметическое дисперсий всех n различных вариантов опытов:
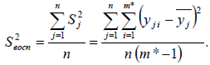(1.15)
Прежде чем производить объединение дисперсий, следует убедиться в их однородности. Проверка производится с помощью критерия Фишера или Кохрена. Для оценки значимости коэффициентов прежде всего находят дисперсию коэффициентов регрессии. Учитывая свойства 1-3 плана, представленного в табл. 1, при одинаковом дублировании опытов по точкам с числом повторных опытов m* получим
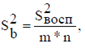(1.16)
а при отсутствии дублирования будем иметь
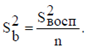(1.16а)
Следовательно, все коэффициенты уравнения регрессии ПФЭ имеют одинаковую точность (дисперсию). В этом заключается принципиальное отличие коэффициентов уравнения регрессии, полученных по плану табл.1, от коэффициентов уравнений, полученных пассивным экспериментом. Планы, по результатам которых коэффициенты уравнения регрессии определяются с одинаковой дисперсией, называются ротатабельными. В связи с этим план, представленный в табл.1, является не только ортогональным, но ротатабельным. В дальнейшем проверка значимости каждого коэффициента производится с использованием t-критерия Стьюдента. Статистически незначимые коэффициенты исключаются из уравнения, а остальные коэффициенты при этом не пересчитываются. После этого уравнение регрессии составляется в виде уравнения связи выходного параметра y и переменных Xi, включающего только значимые коэффициенты.
После вычисления коэффициентов уравнения следует прежде всего проверить его пригодность или адекватность. Для этого достаточно оценить отклонение выходной величины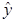 
, предсказанной уравнением регрессии, от результатов эксперимента y в различных точках.
Рассеяние результатов эксперимента относительно уравнения регрессии, аппроксимирующего искомую зависимость, можно, как уже было показано ранее, охарактеризовать с помощью дисперсии адекватности, оценка которой, справедливая при одинаковом числе дублирующих опытов, находится по формуле
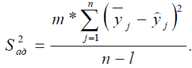(1.17)
Здесь n – число опытов (вариантов); l=k+1, где k – число членов в уравнении регрессии.
Проверка адекватности состоит в выяснении соотношения между дисперсией адекватности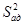 
и дисперсией воспроизводимости 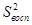и проводится с помощью F-критерия Фишера, который в данном случае рассчитывается как
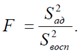(1.18)
Если вычисленное значение критерия меньше теоретического 
для соответствующих степеней свободы m1=n-l, m2=n(m*-1), при заданном уровне значимости α, то описание свойств объекта уравнением регрессии признается адекватным объекту. Адекватность модели может быть достигнута уменьшением интервала варьирования факторов, а если это не дает результата, то переходом к плану второго порядка.