Многошаговые методы. интерполяционные формулы адамса

Рассмотренные методы численного интегрирования дифференциальных уравнений относятся к типу явных методов. То есть для построения последующего шага таблицы, -го шага, использовалась информация о поведении решения и правой части дифференциального уравнения только на предыдущих шагах. Информация о «возможном» поведении решения дифференциального уравнения, при построении методов, не использовалась. Это несколько снижает точность получаемых результатов. Более высокой точностью обладают неявные методы.

Рассмотрим схему построения неявных методов на примере неявного метода Эйлера.

Рис. 8.1. Структурная схема алгоритма решения дифференциального уравнения по схеме Адамса (формула (8.17)).

Интеграл в правой части выражения (8.2) вычислялся по формуле прямоугольников с использованием значения подынтегральной функции в точке 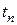. Однако, его можно вычислить, используя значение подынтегрального выражения в точке . Выполняя данную операцию, получаем следующую формулу

. (8.22)

Искомое решение входит в левую, и в правую части выражения (8.22). Для его нахождения выражение (8.22) необходимо рассматривать как нелинейное уравнение относительно переменной 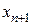вида

, (8.23)

где

.

Найти решение уравнения (8.23) можно, используя любой метод решения нелинейных уравнений, например, метод Ньютона, или метод простых итераций. Отметим, что если дифференциальное уравнение (8.1) является линейным, то уравнение (8.23) также является линейным и значение 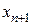находится точно. Отметим также, что в случае решения линейных дифференциальных уравнений высокого порядка, о чем речь пойдет ниже, уравнение (8.23) будет представлять собой систему линейных алгебраических уравнений.

Достоинство данного подхода – предсказание решения на следующем шаге интегрирования.

Рассмотрим интерполяционный метод Адамса. Исходной формулой для получения соответствующих вычислительных схем является формула (8.16). В отличие от экстраполяционного метода, при интерполяционном шагу интегрирования кроме отрицательных значений придают и положительные значения.

Рассмотрим построение вычислительных схем на примерах.

Пусть необходимо получить точность (погрешность), пропорциональную . В этом случае необходимо знать три слагаемые формулы (14), т.е. вычислить два коэффициента: и . Имеем следующую систему уравнений:

,

или

Откуда следует, что

, .

Подставляем найденные значения в формулу (8.14), получаем

,

или

. (8.24)

Найти 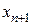из последнего выражения можно, используя любой метод решения нелинейных уравнений.

Выполняя действия по тому же алгоритму, можно получить вычислительные схемы заданной точности.

Для точности , имеем

.

Для погрешности, пропорциональной , имеем

.

Более общая формула, выраженная через конечные разности, имеет вид (интерполяционная формула Адамса):

Также как и экстраполяционную, данную формулу можно также обрывать на любом члене, получая вычислительные схемы различной точности.

Как и в случае экстраполяционной формулы Адамса, для ее использования необходимо заготовить начало таблицы вычислений.

На каждом шаге необходимо находить последующее значение дифференциального уравнения путем решения нелинейного уравнения. Метод решения может быть выбран любым.