Оценка коэффициентов модели Самуэльсона-Хикса

Модель С-Х включает в себя только рынок благ, и поэтому уровень цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен.

Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде

C_t = C_a,t + C_yy_t-1, где C_a - автономное потребление.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде

I_t = I_a,t + 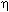(y_t-1 - y_t-2).

На рынке благ установится динамическое равновесие, если

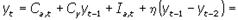
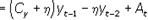
где A_t = С_a,t + I_a,t.

Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

При фиксированной величине автономных расходов (A_t = A = const) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне , т.е. y_t = y_t-1 = y_t-2 = ... = y_t-n = , где n - число периодов с неизменной величиной автономных расходов.

Из уравнения (9.1) следует, что = A/(1 - C_y).

Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.

Освободимся от неоднородности в уравнении (9.1). Значения y_t и удовлетворяют равенству (9.1), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:

,

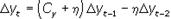(9.2)

где 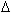y_t y_t - .

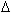Так как y_t = + y_t, то направление изменения y_t определяется направлением изменения y_t.

Из теории решения дифференциальных и конечно-разностных уравнений⁴ следует, что характер изменения 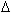y_t зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (C_y + 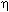)² - 4 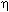, то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.

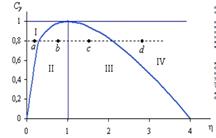
Рис. 9.3. Четыре области сочетаний Cy, η

Если (Cy+η)2-4η>0, то изменение yt происходит монотонно; при (Cy+η)2-4η<0 оно будет колебательным. Следовательно, график функции , изображенный на рис. 9.3, отделяет множество сочетаний Cy, η, обеспечивающих монотонное изменение yt, от множества комбинаций из значений Cy, η, приводящих к колебаниям yt.

Устремляется ли значение yt к некоторой конечной величине или уходит в бесконечность, зависит от значения последнего слагаемого характеристического уравнения. Если η < 1, то равновесие установится на определенном уровне. При η > 1 нарушенное 1 раз равновесие больше не восстановится. Когда η = 1 , тогда значение yt будет колебаться с постоянной амплитудой.

В результате все множество сочетаний C_y и 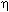оказалось разделенным на пять областей, как это показано на рис. 9.3. Если значения C_y и 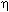указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение y_t монотонно устремится к новому равновесному уровню При значениях C_y и 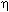, находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений C_y и 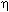, расположенные справа от перпендикуляра, опущенного из точки B на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений C_y, 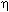указывают на область III, тогда динамика y_t приобретает характер взрывных колебаний. Комбинации значений C_y, 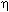в области IV приводят к тому, что после нарушения равновесия y_t монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания y_t.