Следует провести расчеты, разобранные в примере 2.1, с вашими условиями

Пример 2.1 Задана система линейных алгебраических уравнений

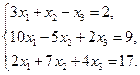
Требуется

1. Ввести в компьютер массивы исходных данных матрицу системы 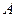и столбец свободных членов 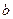, установить 1 в качестве начала отсчета индексов массивов. Вычислив определитель, проверить невырожденность матрицы .
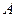2. Составить расширенную матрицу 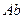, сравнив её ранг с рангом матрицы 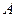и с числом неизвестных, сделать вывод о совместности и определенности системы .
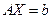3. Перед каждым шагом прямого хода производить сортировку уравнений так, чтобы коэффициенты при исключаемых неизвестных располагались сверху вниз по порядку убывания модулей. Это позволит избежать появления нулевых коэффициентов на главной диагонали
4. С помощью элементарных преобразований над строками расширенной матрицы 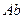провести последовательное исключение неизвестных по шагам прямого хода метода Гаусса.
5. Вычислить определитель системы по диагональным элементам расширенной матрицы в конце прямого хода.
6. Осуществив преобразования обратного хода, получить решение системы.
7. Сравнить полученные результаты с результатами применения встроенных функций.

Решение.Привычное для нас начало счета индексов элементов массивов с единицы устанавливается командой «ORIGIN:=1», по умолчанию индекс первого элемента массива равен нулю. Ранг матрицы M вычисляется функцией 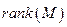. Программа решения системы приведена на рис. 2.1 - 2.3.

Рис. 2.1

Нажатием кнопки 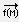на панели Матрицы или клавиш “Ctrl”+”-“ можно обеспечить поэлементное проведение операции над матрицами. В знак этого сверху над функцией появится стрелка как над вектором. Вместо модуля вектора-столбца появится вектор-столбец, составленный из модулей компонент исходного вектора. Функция 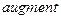присоединяет полученный вектор к расширенной матрице в качестве последнего столбца. Затем функция 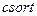сортирует строки полученной матрицы 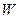по возрастанию элементов последнего столбца и, наконец, функция 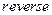меняет порядок элементов последнего столбца на противоположный – по убыванию. В результате таких комбинаций мы получим в качестве разрешающего элемента на главной диагонали элемент, самый большой по модулю в столбце. Удалив последний столбец с помощью функции 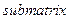, мы получим расширенную матрицу, подготовленную к очередному шагу прямого хода Гаусса.

В начале каждого шага процесса Гаусса мы транспонируем расширенную матрицу и обозначаем её как 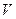. Вместо преобразования строк расширенной матрицы мы работаем с векторами-столбцами 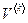. Номера преобразуемых столбцов задаются ранжированной переменной: 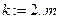- на первом шаге, 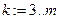- на втором шаге и т.д. Формулы преобразований соответствуют формулам (2.4). В конце каждого шага 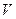транспонируется, чтобы можно было удостовериться, что очередной столбец ниже главной диагонали заполнился нулями. При окончании прямого хода мы можем очень экономичным образом вычислить определитель матрицы 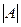. Он равен произведению элементов, стоящих на главной диагонали в преобразованной расширенной матрице, если, разумеется, не было перестановок уравнений. Для вычисления определителя можно использовать кнопку 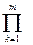в панели Calculus(Анализ). Затем, используя ранжированную переменную 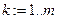, делим каждую строку на её диагональный элемент. Прямой ход закончен, переходим к обратному ходу, осуществляемому аналогичным образом. Здесь нулями заполняется треугольник над главной диагональю, на каждом шаге обратного хода используются убывающие ранжированные переменные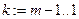 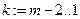и т.д. Данное решение следует сравнить с решениями, полученными с использованием функци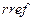й и .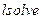

Эти функции построены профессионалами на основе метода Гаусса. Наша программа, приведенная на рис. 2.1 - 2.2, носит учебный характер. В заключение порекомендуем для облегчения набора использовать операцию копирования на каждом шаге с внесением необходимых изменений.

Рис. 2.2

Рис. 2.3

Перейдем к итерационным методам решения систем линейных алгебраических уравнений, ограничимся проблемой нахождения единственного решения определенной системы

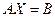(2.9)

Здесь 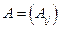- квадратная матрица 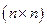коэффициентов системы; 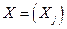- матрица 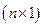неизвестных; 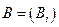- матрица 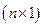свободных членов. Ранг системы равен числу неизвестных .

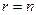Различные варианты метода простых итераций предполагают переход от системы (2.9) к эквивалентной системе

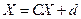(2.10)

Задачу о поиске точного решения 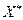систем (2.9) или (2.10) трактовать как задачу о неподвижной точке линейного отображения 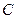в 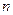- мерном пространстве. Итерационный процесс, определяющий последовательность приближений 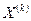к неподвижной точке 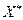, определяется очевидным рекуррентным соотношением

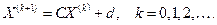. (2.11)

Начальное приближение 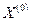считается известным. Итерационный процесс (2.11) принято называть методом простых итераций.

Необходимым и достаточным условием сходимости процесса простых итераций к точному решению 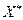при любом начальном приближении 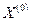является требование, чтобы все собственные значения матрицы по модулю были меньше 1. [вержбицкий]

Более простым достаточным условием сходимости служит требование

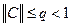. (2.12)

Из (2.17) следуют полезные оценки погрешности приближений: апостериорная оценка

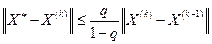, (2.13)

которую используют для остановки процесса при достижении заданной точности, и более грубая априорная оценка:

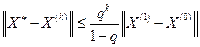, (2.14)

по которой до проведения расчетов можно найти число итераций, необходимое для достижения заданной точности. Отметим, что в данных оценках предполагается использование согласованных матричных и векторных норм.

Различные варианты метода простой итерации различаются способом перехода между системами (2.9) и (2.10). Рассмотрим метод, предложенный немецким математиком Карлом Якоби (1804-1851). Представим матрицу 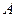исходной системы (2.9) в виде суммы матриц: диагональной матрицы 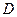и двух строго треугольных с нулевой диагональю 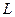и 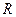(левой и правой). Тогда система (2.9) запишется в виде

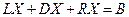(2.15)

и если на главной диагонали исходной матрицы не было нулей, то у 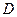существует обратная матрица 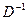- диагональная матрица с диагональными элементами 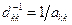. Тогда мы можем преобразовать (2.9) в систему (2.10), где

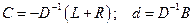. (2.16)

Метод итераций Якоби в матричном виде определяется рекуррентной формулой (2.11) с матрицами (2.16). Отметим, что в матрице на главной диагонали стоят нули. Выпишем рекуррентную формулу Якоби в развернутом виде:

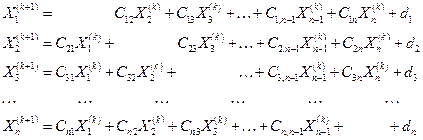(2.17)

Доказано простое достаточное условие сходимости последовательности итераций Якоби, которое называют диагональным преобладанием:

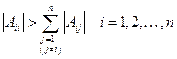(2.18)

Другой немецкий ученый – астроном и математик Людвиг Зейдель (1821-1896) предложил, как усовершенствовать метод Якоби и ускорить сходимость. Для этого на каждом шаге итераций нужно уже найденную из первого соотношения (2.17) компоненту 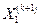следующего приближения подставить в правую часть второго соотношения. Затем уже найденные компоненты 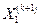и 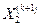следующего приближения подставить в правую часть третьего соотношения и т.д. В итоге получаем рекуррентные формулы известные как формулы Зейделя:

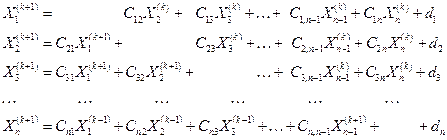(2.19)

Сравним оба метода - метод Якоби:

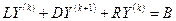(2.20)

и Зейделя:

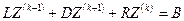. (2.21)

в неявной матричной форме. Сопоставление (2.20) и (2.21) показывает, что оба метода сводятся к методу простой итерации (2.11), только матричные коэффициенты вычисляются по разным формулам. Для того, чтобы не было путаницы выпишем рекуррентную формулу Якоби еще раз:

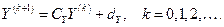. (2.22)

Здесь коэффициенты определяются формулой (2.15), следующей из (2.20)

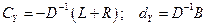. (2.23)

И, наконец, запишем рекуррентную формулу Зейделя:

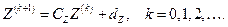. (2.24)

Здесь коэффициенты определяются формулой, следующей из (2.21):

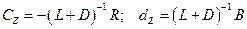. (2.25)

Доказано, что условие диагонального преобладания (2.18) является достаточным условием сходимости не только для метода Якоби, но и для метода Зейделя, причем для метода Зейделя оно обеспечивает более быструю сходимость [ Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. - М.: Высшая школа, 2000.].

Отметим еще один важный класс систем (2.9) с симметричной положительно определенной матрицей (так называемые нормальные системы), для которых метод Зейделя сходится. [ Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970.] Там же доказано, что если любая невырожденная матрица 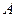при умножении слева на транспонированную матрицу 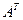становится симметричной положительно определенной, а значит система (2.9) переходит в нормальную систему

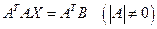. (2.26)

Такое преобразование системы называют симметризацией Гаусса [ Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. - М.: Высшая школа, 2000.]