Общие понятия о выборочном наблюдении, его преимущества
Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.
По понятным причинам выборочный метод может широко использоваться органами государственной статистики. Он позволяет при значительной экономии средств и затрат получать необходимую достоверную информацию. Гарантия репрезентативности обеспечивается применением научно обоснованных способов отбора единиц, которые подлежат обследованию.
Следует сразу же иметь в виду, что при сопоставлении показателей по результатам выборочного исследования с характеристиками для всей генеральной совокупности могут иметь место отклонения. Величина этих отклонений называется ошибкой наблюдения, которая может быть или ошибкой регистрации (несовершенство технических условий), или ошибкой репрезентативности (случайное или систематическое нарушение правил при отборе единиц).
В статистике приняты следующие условные обозначения:
N - объем генеральной совокупности;
п - объем выборочной совокупности;
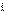 - средняя в генеральной совокупности;
- средняя в генеральной совокупности;
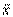 - средняя в выборочной совокупности;
- средняя в выборочной совокупности;
р - доля единиц в генеральной совокупности;
w - доля единиц в выборочной совокупности;
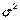 - генеральная дисперсия;
- генеральная дисперсия;
S2 - выборочная дисперсия;
 - среднее квадратическое отклонение признака в генеральной совокупности;
- среднее квадратическое отклонение признака в генеральной совокупности;
S - среднее квадратическое отклонение признака в выборочной совокупности
34. статистический график – это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. При построении графического изображения следует соблюдать ряд требований. Прежде всего график должен быть достаточно наглядным, так как весь смысл графического изображения как метода анализа в ом и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Для выполнения вышеперечисленных требований каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; эксплуатацию графика.
Рассмотрим подробнее каждый из указанных элементов. Графический образ (основа графика) – это геометрические знаки, т.е. совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. Важно правильно выбрать графический образ, который должен соответствовать цели графика и способствовать наибольшей выразительности изображаемых статистических данных. Графическими являются лишь те образы, в которых свойства геометрических знаков – фигура, размер линий, расположение частей – имеют существенное значение для выражения содержания изображаемых статистических величин, причем каждому изменению выражаемого содержания соответствует изменение графического образа.
Поле графика – это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от его назначения.
Пространств ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространенной является система прямоугольных координат. Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика – это мера перевода числовой величины в графическую.
Последний элемент графика – экспликация. Каждый график должен иметь словесное описание его содержания. Оно включает его содержание; подписи вдоль масштабных шкал и пояснения к отдельным частям графика.
Существует множество видов графических изображений .Их классификация основана на ряде признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели; в) задачи, решаемые с помощью графического изображения. г) задачи, решаемые с помощью графического изображения.
По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы- это графики количественных отношений. Существуют диаграммы : сравнения, динамики и структурные. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д. При этом сравнения исследуемых совокупностей производится по какому –либо существующему варьирующему признаку. Статистические карты – графики количественного распределения по поверхности. Виды стат карт- картограммы и картодиаграммы. По свей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т.е. показывают пространственное размещение или пространственную распространенность статистических данных. Геометрические знаки - это либо точки, либо линии или плоскости, либо геометрические тела. В соответствии с этим различают графики точечные, линейные, плоскостные и пространственные (объемные).
При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных – линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются на столбиковые, полосовые, круговые, квадратные и фигурные.
В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные диаграммы и диаграммы динамики.
Особым видом графиков являются диаграммы распределения величин, представленных вариационным рядом. Это гистограмма полигон, огива, кумулята.
1.Предмет статистики, ее взаимосвязь с другими зкономическими науками.
2. Сущность основ понятий стат науки: стат совокупность, единица совокупности, стат показатель, признак, интервал, вариация.
3.Зтапьі статистического исследования.
4. Формьі, видьі и способи проведення статистического наблюдения.
5. Понятия и основньїе злементн статистической сводки и группировки.
6. Стат группир и их види. Вторичн группировки.
7. Ряди распределения и их види.
8Графики рядов распределения.
9 Сущность, злементн и види статистических таблиц.
10 Абсолютнне величини и их види.
11 Относительнне величини и их види.
12 Сущность средних величин.
13. Особенности расчета средних величин. Метод моментов.
14. Распределительнне средние величини.
15Сущность и показатели вариации.
16Понятие и види рядов динамики.
17 Показатели характер рядов динамики: средн уровень ряда, абсол и средн абсол прирост, козффиц роста и козф прироста, абсол значение одного % прироста.
18 Сущность и назначение методов укрупнення интервалов и скользящей средней. Методи установлення тенденций.
19 Сущность и назначение метода аналитического вьіравнивания.
20 Способи приведення рядов динамики и сопоставимому виду.
21 Понятие индивидуальних и общих индексов, цепнне и базиснне индексщ, их взаимосвязь.
22Системи взаимосвязанннх агрегатних индексов.
23 Системи агрегатних индексов Пааше и Ласпейреса.
24 Средневзвешеннне агрегатнне индекси.
25 Сущность и назначение методов цепних постановок и абсолютних разниц.
26. Сущность и назначение индексов средних величин.
27.Функцион, стохастич и корреляцион взаимосвязи между явлен и процес.
28 Методи установл взаимосв между процессами и явленнями.
29 Непараметрич методи установлення взаимосвязей между процессами и явленнями.
30Стат гипотеза, ее проверка.
31. Общие понятия о внборочн наблюд, его преимущ.
32. Установление ошибки вьіборки.
33 Способи отбора, обеспечивающие репрезентативность вьіборки: случайннй, механический, типологический.
34 Сущность, назначение и основньїе злем стат графиков. Види стат графиков.
