Законы сохранения импульса и энергии

Программа по общему курсу физики

Раздел «Механика».

Кинематика

Предмет физики. Методы физического исследования. Связь между физикой и техникой. Связь физики с математикой и другими науками. Международная система единиц. Физические основы механики. Предмет механики. Разделы механики. Механическое движение и его относительность. Система координат и система отсчёта. Инерциальные системы отсчёта. Механический принцип относительности. Преобразование Галилея. Кинематика материальной точки. Понятие траектории. Уравнение движения. Вектор перемещения. Путь. Скорость. Относительность скорости. Классический закон сложения скоростей. Равномерное прямолинейное движение. Ускорение. Касательное и нормальное ускорения. Движение точки по окружности. Угловое смещение, угловая скорость. Равномерное движение точки по окружности. Число оборотов, частота и период вращения. Угловое ускорение. Равнопеременное движение точки по окружности. Связь между линейными и угловыми кинематическими величинами. Поступательное и вращательное движение твёрдого тела.

Динамика материальной точки

Первый закон Ньютона. Импульс частицы – векторная мера механического движения. Понятие силы. Второй закон Ньютона. Масса – мера инертности частицы. Интегральная форма основного закона механики. Действие силы во времени. Понятие момента силы. Принцип независимости действия силы. Понятие о равнодействующей. Действие силы в пространстве. Кинетическая энергия – скалярная мера механического движения. Понятие работы как формы передачи кинетической энергии. Теорема кинетической энергии. Формула работы. Понятие мощности. Понятие момента силы относительно точки. Момент импульса материальной точки. Теорема о моменте импульса.

Классификация взаимодействий

Фундаментальные и нефундаментальные законы взаимодействия. Консервативные и неконсервативные взаимодействия. Гравитационное взаимодействие. Закон всемирного тяготения. Масса – мера тяготения. Поле тяготения Земли. Понятие силы тяжести и веса тела. Эквивалентность «инертной» и «тяжёлой» массы частицы (тела). Работа силы тяжести. Потенциальная энергия тяготения. Силы трения. Внешнее и внутреннее трение. Трение покоя, скольжения и качения. Вязкое трение. Силы сопротивления. Силы упругих деформаций. Виды деформаций. Закон Гука для упругих деформаций. Потенциальная энергия упругих деформаций.

Динамика системы материальных точек (частиц)

Импульс системы материальных точек. Закон сохранения импульса системы материальных точек. Третий закон Ньютона. Кинематическое определение инертной массы. Центр инерции системы материальных точек. Закон аддитивности массы. Основной закон механики системы материальных точек. Механическая энергия системы частиц – скалярная мера механического движения и взаимодействия частиц. Кинетическая энергия системы частиц. Потенциальная энергия взаимодействия частиц. Закон сохранения механической энергии. Теорема о потенциальной энергии. Связь между силой и потенциальной энергией. Потенциальные кривые. Финитное и инфинитное движение.

Динамика вращательного движения твёрдого тела

Кинетическая энергия вращения твёрдого тела. Понятие момента инерции относительно оси вращения. Момент инерции различных тел (стержень, цилиндр, диск, шар) относительно оси вращения, проходящей через центр масс. Теорема Штейнера. Понятие момента силы относительно оси вращения. Работа момента силы. Понятие момента импульса тела относительно неподвижной оси вращения. Закон сохранения момента импульса тела и изотропность пространства.

Колебания

Гармонические колебания. Амплитуда, фаза, частота и период колебаний. Дифференциальное уравнение гармонических колебаний. Пружинный, математический и физический маятники. Энергия гармонических колебаний. Затухающие колебания. Дифференциальное уравнение затухающих колебаний. Декремент затухания. Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Явление резонанса.

Элементы специальной теории относительности (СТО). Постулаты теории относительности. Преобразования Лоренца. Относительность одновременности. Релятивистские эффекты замедления времени, сокращения длин. Релятивистский закон сложения скоростей. Релятивистская динамика. Основной закон релятивистской динамики материальной точки. Зависимость массы от скорости. Эквивалентность энергии и массы. Связь между импульсом и энергией в СТО. Граница применимости классической механики.

Кинематика

Положение материальной точки в пространстве задается радиус-

вектором :

,

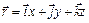где - единичные векторы, x,y,z- декартовы координаты точки.

Быстроту изменения положения точки в пространстве с течением времени характеризует скорость.

Средняя скорость

,

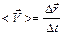где - перемещение точки за время Dt.

Мгновенная скорость

,

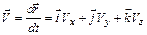где .

Модуль скорости

Быстроту изменения вектора скорости с течением времени характеризует ускорение.

Среднее ускорение

.

Мгновенное ускорение

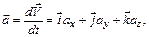
где .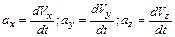

При движении точки вдоль оси OX

;

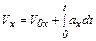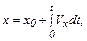
где V_0X и х₀ - скорость и координата в момент времени t=0.

При равнопеременном движении(a_X=const) вдоль оси ОХ

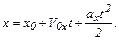
В случае криволинейного движения

,

где 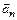- нормальное ускорение, характеризует изменение скорости по направлению и направлено к центру кривизны в данной точке траектории; - тангенциальное ускорение, характеризует изменение скорости по величине и направлено вдоль касательной в данной точке траектории.

Модуль полного ускорения

,

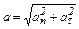где 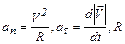- радиус кривизны траектории.

Положение твердого тела при вращении вокруг оси определяется углом поворота j.

Средняя угловая скорость

где Dj - изменение угла поворота за интервал времени Dt.

Мгновенная угловая скорость

Угловое ускорение

Кинематические уравнения при вращении твердого тела:

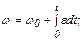
где w₀ и j₀ - начальные угловая скорость и угол поворота.

При равнопеременном вращении

.

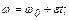
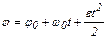Связь между линейными и угловыми величинами, характеризующими движение точки:

; .

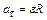примеры решения задач

Задача 1. Движение материальной точки задано уравнением 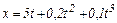(м). Определить скорость точки в моменты времени t₁=2 с и t₂=4 с, а также среднюю скорость в интервале времени от t₁ до t₂.

Точка прямолинейно движется вдоль оси OX. Модуль мгновенной скорости в этом случае

(м/с).

Найдем V₁ и V₂:

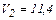, м/с;

, м/с.

Средняя скорость

где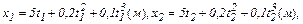

м/с.

Ответ: V₁=7 м/с, V₂=11,4 м/с, м/с.

Задача 2. С башни высотой Н = 25 м бросили камень со скоростью V₀ = 15 м/с под углом a = 30⁰ к горизонту. Через какое время t_п и на каком расстоянии S от основания башни камень упадет на землю?

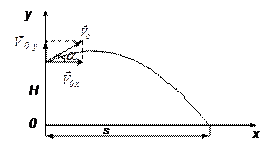Начало отсчета возьмем у основания башни.

Ось OY направим вертикально вверх, ось OX – горизонтально. Движение камня вдоль оси OX равномерное, вдоль оси OY – равнопеременное:

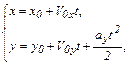
где 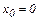, 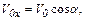y₀=H , ,

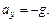
Общие уравнения движения камня в выбранной системе отсчета примут вид

В момент падения камня t=t_n, x=S, y=0.

(1)   (2)

Решая квадратное уравнение (2), найдем t_n=3,1c.

Подставим t_n в (1), получим S=41м.

Ответ: t_n=3,1с, S=41м.

Задача 3. Небольшое тело движется по окружности радиусом R со скоростью V=kt где k=const. Найти зависимость полного ускорения от времени.

На рисунке покажем полное ускорение тела и его составляющие.

, ;

.

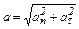Модуль тангенциального ускорения

.

Модуль нормального ускорения

.

Модуль полного ускорения

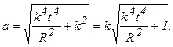
Ответ: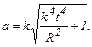

Задача 4. Найти величину углового ускорения лопатки турбины, расположенной на расстоянии R от оси вращения, через время t₁ после пуска турбины. Зависимость линейной скорости лопатки от времени выражена уравнением где a и b - постоянные коэффициенты. Найти число оборотов N₂ через время t₂ после пуска турбины. Принять j₀=0.

Угловое ускорение

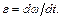
Используем связь угловой скорости с линейной:

.

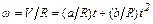Найдем зависимость углового ускорения от времени:

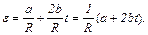
В момент времени

.

Угловая скорость

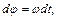
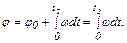
Выразив угол j через число оборотов (j=2pN₂) и зная w как функцию времени, получим

Число оборотов лопатки

Ответ: ; .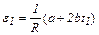

задачи для самостоятельного решения

1.1. Свободно падающее тело последние 196 м пути прошло за 4 с. Найти время падения.

1.2. Во сколько раз отличается время движения катера туда и обратно по реке и по озеру? Скорость течения реки 3 км/ч, скорость катера относительно воды в обоих случаях 9 км/ч. Расстояние считать одинаковым.

1.3. С какой высоты упало тело, если последний метр своего пути оно прошло за время t = 0,1 с?

1.4. Два тела свободно падают с разных высот и достигают земли одновременно. Первое тело падало в течение 2 с, второе - 1 с. На какой высоте было первое тело, когда второе начало падать?

1.5. С балкона бросили мяч вертикально вверх с начальной скоростью V₀ = 5 м/с. Через время τ = 2 c мяч упал на землю. Определить высоту балкона и модуль скорости мяча вмомент удара о землю.

1.6. Два тела брошены вертикально вверх из одной точки, одно за другим, через время τ = 2 с с начальной скоростью V₀₁ = V₀₂ =29,4 м/с. Через какое время после бросания первого тела они встретятся?

1.7. Свободно падающее тело в последнюю секунду проходит половину всего пути. Определить высоту, с которой падает тело, и продолжительность его падения.

1.8. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h = 8,75 м два раза с интервалом ∆t = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость тела.

1.9. Тело брошено вертикально вверх с начальной скоростью V₀ = 4 м/с. Когда оно достигло верхней точки полета, из того же начального пункта с той же начальной скоростью V₀ вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

1.10. Материальная точка движется прямолинейно с ускорением а=5 м/с². Определить, на сколько путь, пройденный в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять V₀ = 0.

1.11. Поезд метро проходит перегон 2 км за 2 мин 20 с. Максимальная скорость поезда 60 км/ч. В начале и конце перегона поезд движется с постоянными ускорениями, равными по абсолютной величине. Определить эти ускорения.

1.12. Два тела свободно падают одно за другим с одной и той же высоты с интервалом времени τ. Через какое время от начала падения первого тела расстояние между ними будет равно r?

1.13. Наблюдатель стоит в начале электропоезда. Первый вагон прошел мимо него за время τ =1 с. Какое время будет двигаться мимо него седьмой вагон? Движение поезда равноускоренное, его начальная скорость V₀ = 0.

1.14. Камень брошен вертикально вверх с начальной скоростью

V₀ = 20 м/с. Через сколько секунд камень будет находиться на высоте

h = 15 м? Какова будет скорость V камня на этой высоте? Сопротивлением воздуха пренебречь.

1.15. С вышки бросили камень в горизонтальном направлении. Через время τ = 2 c он упал на землю на расстоянии S = 40 м от основания вышки. Определить начальную V₀ и конечную V скорости камня.

1.16. Горизонтально брошенный мяч ударяется о стенку, находящуюся на расстоянии S = 5 м от нее. Высота места удара мяча о стенку на 1 м меньше высоты, с которой брошен мяч. Под каким углом α мяч подлетает к поверхности стенки? Сопротивление воздуха не учитывать.

1.17. Тело брошено под углом к горизонту. Наибольшая высота подъема и радиус кривизны траектории движения тела в верхней точке траектории равны 3 м. Найти начальную скорость тела и угол, под которым его бросили. Сопротивление воздуха не учитывать.

1.18. Дальность полета тела, брошенного горизонтально со скоростью V₀ = 9,8 м/с, равна высоте, с которой брошено тело. Чему равна эта высота?

1.19. Тело, брошенное под углом α = 30⁰ к горизонту, дважды было на одной и той же высоте h: спустя t₁ = 10 с и t₂ = 50 с. Определить начальную скорость тела и высоту его подъема.

1.20. Пуля пущена с начальной скоростью V₀ = 200 м/с под углом α = 60⁰ к горизонту. Определить максимальную высоту подъема h и радиус кривизны траектории R пули в ее наивысшей точке.

1.21. Тело брошено под некоторым углом α к горизонту. Найти величину этого угла, если горизонтальная дальность полета тела S в 4 раза больше максимальной высоты траектории h.

1.22. Камень брошен горизонтально. Через время t = 3 с вектор его скорости образует с горизонтом угол α = 60⁰ . Какова была начальная скорость V₀ камня?

1.23. Камень брошен под углом α = 60⁰ к горизонту cо скоростью V₀ =19,6 м/с. Вычислить нормальную составляющую ускорения камня через время τ = 0,5 с после начала движения.

1.24. Дальность полета тела, брошенного горизонтально со скоростью V₀ = 9,8 м/с, равна высоте, с которой брошено тело. Под каким углом к α горизонту тело упадет?

1.25. Мальчик бросает мяч со скоростью V₀ = 10 м/с под углом α = 45⁰ к горизонту. На какой высоте мяч ударится о стенку, если она находятся на расстояния S = 3 м от мальчика?

1.26. С башни высотой h = 20 м горизонтально бросают мяч со скоростью V₀ = 10 м/с. На каком расстоянии S от башни мяч упадет на землю?

1.27. Маховик начал вращаться равноускоренно и за время τ = 10 с его частота стала n = 300 об/мин. Найти угловое ускорение маховика и число оборотов, которое он сделал за это время.

1.28. Точка движется по окружности радиусом R = 10 м с постоянным тангенциальным ускорением а_τ, если известно, что к концу пятого оборота скорость точки V = 79,2 см/с. Найти а_τ.

1.29. Колесо автомашины вращается равноускоренно. После 50 полных оборотов частота вращения колеса возросла от n₁ = 4 об/с до n₂ = 6 об/с. Определить угловое ускорение колеса e.

1.30. Движение точки по окружности радиусом R = 200 см задано уравнением S = 2t³ (м). В какой момент времени нормальная составляющая ускорения a_n точки будет равна ее тангенциальной составляющей a_τ? Определить полное ускорение а в этот момент.

1.31. Движение точки в плоскости XY задано уравнениями X = 2t–0,5t³ (м), Y = 2t – t² (м). Определить скорость точки V к концу второй секунды.

1.32. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени нормальная составляющая ускорения a_n= 4,0 м/с², а векторы полного и нормального ускорений образуют угол α = 60⁰. Найти скорость и тангенциальную составляющую ускорения точки.

1.33. Движение точки по окружности радиусом R = 4 м задано уравнением S = 10 + t² - 2t. Найти тангенциальное a_τ, нормальное a_n и полное а ускорения точки в момент времени t = 2 с.

1.34. Движение материальной точки задано уравнением Х = 4t - - 0,05t². Определить момент времени, в который скорость точки равна нулю. Найти координату и ускорение точки в этот момент. Построить графики зависимости координаты, пути, скорости и ускорения этого движения от времени.

1.35. Путь, пройденный телом, задан уравнением S = 2t – t² + t³ (м). Найти среднюю скорость тела в интервале от 1 до 5 с.

1.36. Путь, пройденный телом, задан уравнением S = 2 + 12t - -6t² + 4t³ (см). Найти среднее ускорение тела в интервале от 1 до 4 с.

1.37. Путь, пройденный точкой поокружности радиусом R = 7 см, задан уравнением S = 4 + 2t + 0,5t² (см). Определить полное ускорение a точки к концу пятой секунды.

1.38. Частота маховика уменьшалась с n₀ = 10 об/с до n = 6 об/с. За время торможения он сделал N = 50 оборотов. Определить угловое ускорение маховика e и продолжительность торможения t.

1.39. Тело вращается вокруг неподвижной оси. Угол поворота задан уравнением φ = 6t -2t³. Найти угловое ускорение тела e в момент его остановки.

1.40. Точка движется по окружности радиусом 20 см с постоянным тангенциальным ускорением 5см/с². Через какое время после начала движения нормальное ускорение точки станет в 2 раза больше тангенциального?

1.41. Диск радиусом R = 0,2 м вращается вокруг фиксированной оси, проходящей через его геометрический центр. Зависимость угла поворота от времени задана уравнением φ = 3 + 0,1t³ - t. Определить для момента времени t = 5 с тангенциальное а_τ, нормальное a_n и полное а ускорения точек на краю диска.

1.42. Точка движется по окружности с угловым ускорением ε ~ t. При t = 0 угловая скорость ω = 0. Модуль нормального ускорения точки a_n ~ t^k. Найти значение показателя k.

1.43. Зависимость угла поворота тела вокруг неподвижной оси от времени задана уравнением φ = A + Bt + Ct² , где A = 10 рад, B = 20 рад/c, С = -2 рад/c². Найти для момента времени t = 4 c полное ускорение точки, находящейся на расстоянии R = 1 м от оси вращения.

1.44. На цилиндр радиусом R = 4 см, который может вращаться около неподвижной горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. За время t = 3 с грузик опустился на высоту h =1,5 м. Определить угловое ускорение цилиндра.

1.45. Точка движется по окружности радиусом R = 20 см с постоянным тангенциальным ускорением a_τ = 5 cм/с². Через какое время после началадвижения нормальная составляющая ускорения a_n = 2a_τ ?

1.46. Камень брошен с начальной скоростью V₀ = 19,6 м/с под углом α = 30⁰ к горизонту. Определить радиус кривизны траектории движения R в высшей ее точке.

1.47. Тело брошено со скоростью V₀ = 19,6 м/с под углом α = 30⁰ к горизонту. Определить нормальную составляющую ускорения тела а_п через время τ = 1,5 с после начала движения.

1.48. Камень брошен горизонтально со скоростью V₀ = 9,8 м/с. Чему равна нормальная составляющая ускорения камня а_п через две секунды после начала его движения?

1.49. Тело брошено под углом к горизонту. Радиус кривизны траектории движения тела и его скорость связаны соотношением R ~ V^k. Найти значение показателя степени k. Сопротивлением воздуха пренебречь.

1.50. Тело брошено под углом к горизонту. Нормальная составляющая ускорения и скорость тела связаны соотношением а_п ~ V^k. Найти значение показателя степени k. Сопротивлением воздуха пренебречь.

1.51. Лодка стоит на расстоянии S = 8 м от отвесного берега реки. Высота берега h = 6 м. С берега на лодку бросают груз. С какой скоростью V₀ надо бросить груз, чтобы его скорость при ударе о лодку была минимальной? Под каким углом a к горизонту необходимо бросить груз?

1.52. Мяч бросают в стенку, находящуюся на расстоянии S = 20 м c начальной скоростью V₀ = 20 м/с. Какой наибольшей высоты при ударе о стенку может достичь мяч? Под каким углом к горизонту его надо бросать в этом случае?

1.53. С башни высотой h = 10 м со скоростью V₀ = 10 м/с бросают мяч. На какое наибольшее расстояние от основания башни может улететь мяч? Под каким углом a к горизонту его надо в этом случае бросать?

1.54. Шарик падает без начальной скорости на поверхность наклонной плоскости, составляющей угол α = 30⁰ с горизонтом. Расстояние по вертикали от начального положения шарика до точки удара с плоскость h = 80,0 см. Считая удар шарика о плоскость абсолютно упругим и пренебрегая возможным вращением шарика, найти наибольшее его удаление от плоскости.

1.55. Фонарь висит на расстоянии d = 5 м от стены и отбрасывает на нее световой луч ("зайчик"). Фонарь совершает затухающие колебания, и его угол поворота зависит от времени t по закону φ = φ₀ e^-at sin ωt (φ₀ = π/3, a = 1 c^-1, ω = 1 с^-1). Найти наибольшее смещение "зайчика" от точки О, ближайшей к фонарю. Найти скорость "зайчика" в момент времени t=0.

2. основное уравнение динамики

Уравнение движения материальной точки (второй закон Ньютона) в векторной форме:

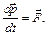
При 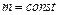уравнение примет вид

.

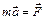В этих уравнениях 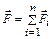- геометрическая сумма сил, действующих на точку, 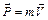- импульс, - масса, 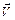- скорость и 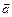- ускорение материальной точки.

примеры решения задач

Задача 1. Тело массой кг движется по вертикальной стене. Сила 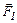действует под углом a = 30⁰ к вертикали. Коэффициент трения 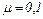. Найти величину силы 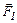, если ускорение тела направлено вверх и равно a = 2 м/с² .

На тело действуют четыре силы: сила 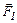, сила тяжести , сила реакции опоры и сила трения . Покажем эти силы на рисунке.

Запишем II закон Ньютона в виде

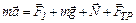. (1)

Ось OY направим вертикально вверх, ось OX – перпендикулярно стене. В проекциях на оси координат уравнение (1) примет вид

OХ: , (2)

OY: . (3)

Сила трения скольжения

. (4)

Используя (2) и (4), перепишем (3):

.

Отсюда

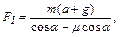
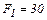Н.

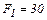Ответ: Н.

Задача 2. В лифте, движущемся вертикально вверх с ускорением 0,2 м/с ², вращается столик с угловой скоростью рад/с. На столике лежит брусок, коэффициент трения равен 0,1. Найти максимальное расстояние между бруском и осью вращения, при котором он удерживается на столике. Принять g = 9,8 м/c ²,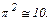

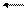
Брусок участвует в двух движениях одновременно: поступательно движется вверх с ускорением 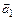и вращается вокруг неподвижной оси с центростремительным ускорением 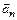. Запишем II закон Ньютона для бруска:

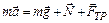, где .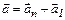

Выберем оси координат OX и OY. В координатной форме основное уравнение движения примет вид

(1)

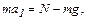(2)

где a_n = w² R, F_TP = μN .

Из (2) N = m (a₁ + g),

F_TP = mm (a₁ + g).

Перепишем (1):

mw²R =mm (a₁ + g).

Получим, что

.

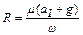После подстановки данных и вычислений R = 0,1 м.

Ответ: R = 0,1 м.

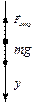Задача 3. С вертолёта, неподвижного висящего на некоторой высоте над поверхностью земли, сброшен груз массой m. Считая, что сила сопротивления воздуха изменяется пропорционально скорости (F_сопр = kV), определить, через какой промежуток времени ускорение груза a₁ = g/2. Коэффициент сопротивления k = const.

Учитывая, что a = dV / dt , F_сопр= kV , получим дифференциальное уравнение первого порядка с разделяющимися переменными:

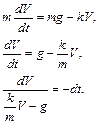
Проинтегрируем:

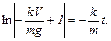
Получим:

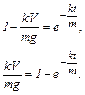
Отсюда

.

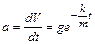В момент времени t = t₁ ускорение a₁ = g/2:

После логарифмирования:

.

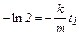Получим

.

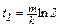Ответ: .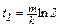

задачи для самостоятельного решения

2.1. Наклонная плоскость, образующая с горизонтом угол α = 30⁰, имеет длину l = 167 см. За какое время тело соскользнет с нее, если коэффициент трения тела о плоскость μ = 0,2?

2.2. Автомобиль массой m = 2,5 т поднимается в гору (α = 30⁰) ускоренно и за время t = 5 мин проходит путь S = 9 км. Начальная скорость автомобиля V₀ = 1 м/с, а коэффициент трения μ = 0,1. Какова сила тяги мотора автомобиля F?

2.3. Брусок соскальзывает с наклонной плоскости, образующей с горизонтом угол α = 30⁰. Каково ускорение бруска, если коэффициент трения его о поверхность плоскости μ = 0,4?

2.4. За какое время тяжелое тело спустится с вершины наклонной плоскости, высота которой h = 2 м, угол наклона α = 45⁰? Предельный угол, при котором тело находится в покое, для этой плоскости равен α_пр = 30⁰.

2.5. Наклонная плоскость образует с горизонтом угол α = 30⁰. Ее длина l = 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t = 2 с. Определить коэффициент трения тела о плоскость μ.

2.6. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. Ее длина l = 2 м, коэффициент трения тела о плоскость μ = 0,2. Какова скорость тела в конце наклонной плоскости, если его начальная скорость V₀ = 0?

2.7. Тело скользит вниз по наклонной плоскости, составляющей с горизонтом угол α = 30⁰. Зависимость пройденного телом расстояния S от времени t дается уравнением S = ct², где с = 1,5 м/с². Найти коэффициент трения тела о плоскость μ.

2.8. На наклонной плоскости длиной l = 13 м и высотой h = 5 м лежит груз массой m = 26 кг. Коэффициент трения груза о плоскость μ = 0,5. Какую силу F надо приложить к грузу: а) чтобы втащить груз; б) чтобы стащить груз?

2.9. Мальчик тянет по горизонтальной дороге санки с грузом. С каким ускорением a движутся санки, если сила тяги F = 200 Н, а веревка образует с горизонтом угол α = 45⁰? Масса санок m = 50 кг. Коэффициент трения полозьев санок μ = 0,1.

2.10. Два связанных груза массами m₁ = 3 кг и m₂ = 5 кг лежат на горизонтальном столе, шнур разрывается при натяжении Т = 24 Н. Какую максимальную силу F можно приложить к грузу массой m₁? Коэффициент трения принять равным μ = 0,2.

2.11. Ракета движется в поле силы тяжести Земли: а) вниз с возрастающей скоростью; б) вверх с торможением. В каждом случае сравнить вес тела, лежащего на полу ракеты, с силой тяжести.

2.12. Шарик массой m висит на нити, которая закреплена. С каким ускорением a и в каком направлении следует перемещать точку подвеса, чтобы натяжение нити было равно половине силы тяжести шарика?

2.13. Через блок перекинута нить, к концам которой привязаны два груза массами m₁ = 1 кг, m₂ = 2 кг. Центры масс грузов находятся на расстоянии h = 1 м друг от друга. За какое время t их центры масс будут на одной высоте?

2.14. Через блок перекинута нить, к концам которой привязаны два груза массой по m = 95 г каждый. На левый груз кладут перегрузок массой m₁ = 7,5 г, а на правый – m₂ = 2,5 г. Какой путь S пройдёт левый груз за t = 2 с? Трением пренебречь.

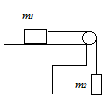2.15. Неподвижный блок укреплен на углу стола. Два груза массами m₁ = 0,5 кг и m₂ = 2 кг соединены нитью, которая, перекинута через блок. Коэффициент трения второго груза о поверхность стола μ = 0,05. Определить силу давления F на ось блока.

2.16. Грузы массами m₁ = 5 кг и m₂ = 2 кг соединены нитью, которая перекинута через блок. Определить коэффициент трения между столом и грузом массой m₂, если ускорение грузов a = 5,4 м/с².

2.17. Невесомый блок укреплен на конце стола. Грузы массами m₁ = 1 кг, m₂ = 2 кг соединены нитью, которая перекинута через блок. Найти коэффициент трения груза m о стол, если сила давления на ось блока F = 1 Н. Трение в блоке мало.

2.18. Невесомый блок укреплен на вершине наклонной плоскости, составляющей с горизонтом угол α = 30⁰. Грузы массами m₁ = 20 кг, m₂ = 12 кг соединены нитью, которая перекинута через блок. Грузы движутся c ускорением a = 4 м/с². Определить коэффициент трения груза массой m₂ о плоскость. Трением в блоке пренебречь.

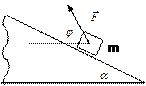
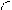2.19. Ящик массой m = 300 кг поднимают равномерно по наклонной плоскости с углом наклона α = 30⁰, прилагая силу, направленную под углом β = 60⁰ к горизонту. Определить эту силу, если коэффициент трения ящика о плоскость μ = 0,1.

2.20. По столу тянут груз при помощи нити, прикрепленной к динамометру. Динамометр показывает 30 Н. Затем тот же груз приводят в движение при помощи нити, перекинутой через невесомый блок, на конце которой висит груз 3 кг. С одинаковым ли ускорением будет двигаться груз?

2.21. Тело массой m движется вверх по вертикальный стене под действием силы F , направленной под углом α к вертикали. Определить, с каким ускорением движется тело, если коэффициент трения тела о стенку равен μ?

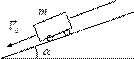2.22. По канатной дороге, идущей с уклоном α = 30⁰ к горизонту, спускается вагонетка массой m = 500 кг. Определить натяжение каната при торможении вагонетки в конце спуска, если скорость вагонетки перед торможением была V₀ = 2 м/с. Коэффициент трения принять равным μ = 0,01.

2.23. Маневровый тепловоз массой M = 100 т тянет два вагона массой по m = 100 т с ускорением a = 0,1 м/с². Найти силу тяги тепловоза F и силу натяжения сцепок T, если коэффициент трения равен m = 0,006.

2.24. Ящик массой m = 10 кг перемещают по полу, прикладывая к нему силу F под углом α = 30⁰ к горизонту. В течение времени τ = 1 с скорость ящика возросла с V₁ = 2 м/с до V₂ = 4 м/с. Коэффициент трения скольжения между ящиком и полом μ = 0,15. Определить силу F.

2.25. Два одинаковых бруска, связанные нитью, движутся по горизонтальной плоскости под действием горизонтальной силы F. Зависит ли сила натяжения нити: а) от массы брусков; б) от коэффициентов трения брусков о плоскость?

2.26. Два шарика а и b, подвешенные на нитях в общей точке, равномерно движутся по круговым траекториям, лежащим в одной горизонтальной плоскости. Сравнить их угловые скорости w.

2.27. На тросе длиной l подвешено тело массой m. На какой максимальный угол можно отклонить его, чтобы при движении груза трос не оборвался? Трос может выдерживать нагрузку, превосходящую силу тяжести тела в n раз.

2.28. Грузик, привязанный к шнуру длиной l = 1,5 м, вращается в горизонтальной плоскости с частотой n = 28 об/мин. Какой угол a с вертикалью образует шнур?

2.29. Велосипедист, движущийся по горизонтальной поверхности со скоростью V = 36 км/ч, описывает мертвую петлю. Определить максимальный радиус петли R.

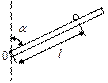
2.30. Шарик лежит на желобе, который может вращаться вокруг оси 0С. Желоб закреплен в т. 0. На каком расстоянии от точки 0 шарик будет в равновесии при вращении желоба с частотой n = 45 об/мин? При этом желоб образует угол α = 45⁰ с вертикалью. Коэффициент трения шарика о желоб μ = 0,2.

2.31. Нить математического маятника отклонили до горизонтального положения и отпустили. Какова минимальная прочность нити F, если масса маятника m?

2.32. Самолет описывает мёртвую петлю радиусом R = 200 м. Во сколько раз сила, с которой летчик давит на сидение в нижней точке петли, больше силы тяжести летчика? Скорость самолета V = 100 м/с.

2.33. Грузик, привязанный к нити длиной l = 1 м, вращается в горизонтальной плоскости. Определить период вращения грузика T если нить отклонилась на угол α = 60⁰от вертикали.

2.34. Сравнить модуль силы натяжения нити математического маятника в крайнем положении с модулем силы натяжения нити конического маятника; длины нитей, массы грузиков и углы отклонения маятников одинаковы.

2.35. Гиря массой m = 100 г вращается на нити в вертикальной плоскости с постоянной скоростью. На сколько отличается сила натяжения нити при прохождении гири через нижнюю и верхнюю точки ее траектории движения?

2.36. Груз массой m = 25 кг подвешен на цепи длиной l = 2,5 м с прочностью на разрыв F = 500 Н. На какой угол a можно отвести груз, чтобы цепь при качаниях груза не разорвалась?

2.37. Дорожка для велосипедных гонок имеет закругление радиусом R = 40 м. В этом месте дорожка сделана с наклоном в a = 30⁰. На какую скорость u рассчитан такой наклон?

2.38. Самолет, летящий со скоростью V = 900 км/ч, делает "мертвую петлю". Каков должен быть ее радиус R, чтобы наибольшая сила давления летчика на сидение была в пять раз больше силы тяжести?

2.39. Гирька, привязанная к нити длиной l = 25 см, вращается в горизонтальной плоскости. Скорость вращения гирьки соответствует n = 2 об/с, масса ее m = 60 г. Найти натяжение нити F.

2.40. Полусферическая чаша радиусом R вращается вокруг вертикальной оси с угловой скоростью ω. В чаше лежит шарик М, вращающийся вместе с нею. В каком месте чаши он находится? (Рассчитать угол α, который характеризует положение шарика).

41. С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом R = 90 м? На какой угол от вертикали a он должен при этом отклониться? Коэффициент трения скольжения μ = 0,4.

2.42. Небольшое тело скользит вниз с вершины сферы радиусом R. На какой высоте h от вершины сферы тело оторвется от её поверхности? Трением пренебречь.

2.43. Автомобиль массой m = 3 т движется с постоянной скоростью V = 36 км/ч по выпуклому мосту радиусом R = 20 м. С какой cилой F давит автомобиль на мост в тот момент, когда линия, соединяющая центр кривизны моста с автомобилем, составляет угол α = 30⁰ c вертикалью?

2.44. С какой минимальной угловой скоростью ω нужно вращать ведерко в вертикальной плоскости, чтобы из него не выливалась вода? Расстояние от поверхности воды до центра вращения равно l.

2.45. Автомобиль движется по выпуклому мосту радиусом R = 40 м. Какое максимальное горизонтальное ускорение может развить автомобиль в высшей точке моста? Скорость его в этой точке V = 50,4 км/ч, а коэффициент трения его колес о мост μ = 0,6.

2.46. Какую минимальную скорость V должен иметь математический маятник, проходя через положение устойчивого равновесия, для того чтобы он мог вращаться по кругу в вертикальной плоскости?

2.47. С какой скоростью V должен въехать велосипедист в нижнюю точку "мертвой петли" радиусом R = 6 м, чтобы не сорваться вниз?

2.48. Привязанную гирю отвели в сторону так, что шнур принял горизонтальное положение, и отпустили. Какой угол a с вертикалью составляет шнур в момент, когда сила натяжения равна силе тяжести гири?

2.49. При насадке маховика на ось центр тяжести оказался на расстоянии r = 0,1 мм от оси вращения. В каких пределах меняется сила давления оси на подшипники, если частота вращения маховика n = 10 об/с. Масса маховика m = 100 кг.

2.50. Сосуд с жидкостью вращается с частотой n = 2 об/c вокруг вертикальной оси. Поверхность жидкости имеет вид воронки. Чему равен угол наклона поверхности жидкости в точках, лежащих на расстоянии r = 5 см от оси?

2.51. Тело соскальзывает с вершины наклонной плоскости, основание которой d = 2,0 м. Коэффициент трения равен μ = 0,25. При какой высоте плоскости время, за которое тело соскользнет с плоскости, будет наименьшим?

2.52. Тело массой m = 50 кг находится на горизонтальной поверхности. Коэффициент трения μ = 0,4. Под каким углом к горизонту α надо приложить к телу силу F = 300 Н, чтобы тело двигалось с наибольшим ускорением? Каково наибольшее ускорение?

2.53. Ведерко с песком и груз в начальный момент времени имеют одинаковую массу m₀ = 0,5 кг и связаны нитью, перекинутой через невесомый блок. При t = 0 из ведерка через отверстие в дне начал высыпаться песок в количестве μ = 50,0 г/с. Пренебрегая трением в блоке, найти, какое расстояние пройдет груз за первые 5 cекунд движения (считать, что за это время песок высыпался не полностью).

2.54. Два связанных веревкой груза массами m₁ = 10,0 кг и m₂ = 20,0 кг тянут по горизонтальной поверхности, прикладывая cилу F = 100 Н к одному из них. Под каким углом a к горизонту надо приложить силу F, чтобы ускорение грузов было наибольшим? Рассчитать наибольшее ускорение, если коэффициент трения грузов о поверхность μ = 0,3.

2.55. На гладкой цилиндрической поверхности радиусом R = 1,0 м лежит гибкий шнур. Верхняя точка поверхности делит шнур на части, длина которых l₁ = π/6 м и l₂ = π/4 м. Шнур расположен перпендикулярно образующей цилиндра, и в момент времени t = 0 его скорость V₀ = 0. Пренебрегая трением, найти ускорение шнура, с которым он начнет соскальзывать с поверхности.

законы сохранения импульса и энергии

Закон сохранения импульса:

,

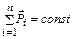где n – полное число тел, входящих в замкнутую систему.

Работа переменной силы

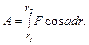
При F =const

A=FDrcosa,

где a- угол между направлениями силы 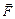и перемещения . Средняя мощность за время Dt

.

Мгновенная мощность

,

где - элементарная работа за промежуток времени dt.

Кинетическая энергия тела при поступательном движении

.

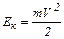Потенциальная энергия тела в поле силы тяжести

,

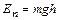где h – высота тела над начальным уровнем отсчёта.

Потенциальная энергия тела при упругой деформации

,

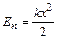где k – коэффициент упругости, x – абсолютная деформация.

В замкнутой системе, где действуют консервативные силы,

E_к+E_п=const.

При действии сил трения необходимо учитывать потери механической энергии.

примеры решения задач

Задача 1. Частица массой m₁, имеющая скорость V₂, налетела на покоящийся шар массой m₂ и отскочила от него со скоростью U₁ под прямым углом к направлению первоначального движения. Какова скорость U₂ шара после соударения? Считать удар центральным.

Используя закон сохранения импульса, получим

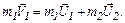
На рисунке покажем импульсы тел.

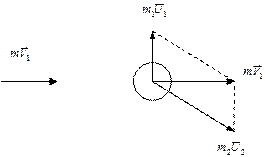Модуль импульса шара найдём, используя теорему Пифагора:

,

отсюда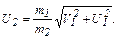

Ответ: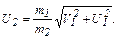

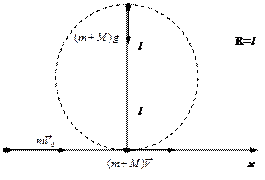Задача 2. Шар массой M висит на нити длиной l. В шар попадает горизонтально летящая пуля и застревает в нём. С какой скоростью V₀ должна лететь пуля, чтобы в результате попадания пули шар мог сделать на нити полный оборот в вертикальной плоскости? Размерами шара пренебречь. В верхней точке сила натяжения нити равна нулю. Масса пули m.

Обозначим: V - скорость шара с пулей сразу после неупругого соударения, U - скорость шара с пулей в верхней точке.

В проекциях на ось OX закон сохранения импульса имеет вид

mV₀ = (m + M) V.(1)

Выберем нулевой уровень отсчёта потенциальной энергии, совпадающий с осью OX .

В нижнем положении шар с пулей обладает только кинетической энергией 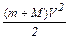; в верхней точке - кинетической и потенциальной (m+M)gh энергиями, где h = 2R =2l.

Закон сохранения механической энергии запишем в виде

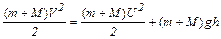. (2)

После преобразований

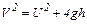. (2¢)

В верхней точке на шар с пулей действует сила тяжести, по условию задачи сила натяжения нити равна нулю. Используем II закон Ньютона:

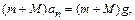(3)

где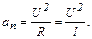

Из уравнения (1) выразим V₀:

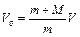_. (4)

Из уравнения (3)

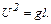(5)

Подставив (5) в (2¢), получим

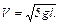
Найдем V₀ , вернувшись к (4)

Ответ: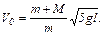

Задача 3. Какова работа силы трения за один оборот аэросаней, движущихся по вертикальной круговой дорожке? Скорость саней постоянна и равна V, масса саней m, коэффициент трения k.

На рисунке покажем все силы, действующие на сани в произвольной точке траектории, учитывая, что , т.к. V=const.

Полная работа силы трения

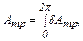где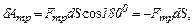

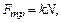
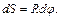
Силу реакции опоры N выразим из уравнения второго закона Ньютона, записанного в проекциях на радиальную ось:

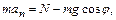
где , R - радиус окружности.

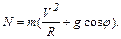
Элементарная работа силы трения

Работа силы трения

После интегрирования

Ответ:

задачи для самостоятельного решения

3.1 .Тело массой m = 2,0 кг падает с высоты h = 20 м из состояния покоя и в момент удара о землю имеет скорость V = 15 м/с. Определить работу силы сопротивления и силу сопротивления, считая её постоянной.

3.2. Какой путь s пройдут санки по горизонтальной поверхности после спуска с горы высотой h = 1,5 м и уклоном α = 45⁰? Коэффициент трения μ = 0,2.

3.3. Ящик тянут равномерно за верёвку. Сила F направлена под углом α = 30⁰. Определить работу, которую при этом совершают. Масса ящика m = 100 кг, коэффициент трения μ = 0,33, путь s = 50 м.

3.4. Поезд из состояния покоя за время τ = 5 мин развивает скорость V = 64,8 км/ч. Масса поезда m = 600 т, коэффициент трения μ = 0,04. Найти среднюю мощность, развиваемую локомотивом, если его движение равноускоренное.

3.5. Какую среднюю мощность развивает автомобиль при подъеме в гору? Начальная скорость автомобиля V₀= 36 км/ч, его конечная скорость V_к= 21 ,6 км/ч, коэффициент трения μ = 0,1, высота горы h = 12 м, длина склона горы l = 80 м, масса автомобиля m = 4×1О³ кг.

3.6. Какую нужно совершить работу A, чтобы пружину жесткостью k = 800 Н/м, сжатую на Dx₁ = 6 см, дополнительно сжать на ∆х₂ = 8 см?

3.7. Санки скатываются с горки высотой h = 8 м по склону длиной l = 100 м. Масса санок с седоком m = 60 кг. Какова сила сопротивления движению санок, если в конце спуска они имели скорость V = 11 м/с?

3.8. Вагонетку массой m = 100 кг поднимают по рельсам в гору с ускорением a = 0,2 м/с². Коэффициент трения колес вагонетки о рельсы μ = 0,1, длина склона горы l = 50 м, угол наклона α = 30⁰. Какова работа A силы тяги?

3.9. Самолет для взлета должен иметь скорость V = 80 км/ч. Длина разбега S = 150 м. Какова мощность моторов при взлете, если масса самолета m = 1000 кг, коэффициент трения колес шасси о землю μ = 0,02?

3.10. На горизонтальном участке пути длиной S = 2 км скорость поезда возросла с V₁ = 36 до V₂ = 72 км/ч. Определить работу и среднюю мощность тепловоза, если масса поезда m = 10³ т, а коэффициент трения m = 0,001.

3.11. Поезд массой m = 10⁶ кг поднимается равномерно со скоростью V = 36 км/ч по уклону в 10 м на 1 км. Коэффициент трения равен m = 0,002. Определить мощность, развиваемую паровозом.

3.12. Какой путь l пройдут до полной остановки санки, имеющие начальную скорость V₀, при подъеме на гору с углом наклона α, коэффициентом трения μ? Известно, что на горизонтальном участке пути с тем же коэффициентом трения μ санки, имеющие такую же начальную скорость V₀, проходят путь l₀.

3.13. Автомобиль массой m = 4 т подъезжает к горке высотой h = 10 м и длиной склона S = 80 м со скоростью V₀ = 36 км/ч. Какую среднюю мощность развивает автомобиль на подъеме, если его скорость на вершине горы при постоянной силе тяги оказалась V = 21,6 км/ч? Коэффициент трения принять равным m = 0,1.

3.14. На подъеме в гору автомобиль движется равномерно со скоростью V = 14,4 км/ч. Какова мощность автомобиля, если его масса m = 6 т, угол наклона горы α = 10⁰, коэффициент трения μ = 0,09?

3.15. Под действием постоянной силы вагонетка прошла путь S = 5 м и приобрела скорость V = 2 м/с. Определить работу силы, если масса вагонетки m = 400 кг и коэффициент трения μ = 0,01.

3.16. Движение тела массой m = 2 кг под действием некоторой силы задано уравнением х = А + Bt + Ct² + Дt³, где А = 10 м, В = -2 м/с, С = 1 м/с², Д = - 0,2 м/с³. Найти мощность, затрачиваемую на движение тела, в моменты времени t₁ = 2 с и t₂ = 5 с.

3.17. На тело массой m = 10 кг, движущееся по горизонтальной плоскости, действует сила F = 100 Н, направленная под углом α = 30⁰ к горизонту. Определить работы всех сил, действующих на тело, а также их суммарную работу при перемещении тела вдоль плоскости на расстояние S = 10 м. Считать, что коэффициент трения μ = 0,1.

3.18. Лифт массой m = 10³ кг поднимается на высоту h = 9 м за время t = 3 с. Сравнить работу по подъему лифта в двух случаях: 1) лифт поднимается равномерно; 2) лифт поднимается равноускоренно. Начальная скорость лифта в обоих случаях V₀ = 0.

3.19. Автомобиль массой m = 2000 кг движется вверх по горке с углом наклона a=10⁰ к горизонту, развивая на пути S = 100 м скорость V = 36 км/ч. Коэффициент трения μ = 0,05; начальная скорость V₀ = 0. Найти среднюю и максимальную мощности двигателя автомобиля при разгоне.

3.20. При вертикальном подъеме груза массой m = 2 кг на высоту h = 1 м постоянной силой была совершена работа А = 78,5 Дж. С каким ускорением a поднимали груз?

3.21. Вагон массой m = 20 т, движущийся равнозамедленно, под действием силы трения равной F = 6000 Н останавливается. Начальная скорость вагона равна V = 54 км/ч. Найти работу силы трения и расстояние, которое вагон пройдёт до остановки.

3.22. Пуля массой m = 10 г подлетает к доске толщиной d = 4 см со скоростью V₁ = 600 м/с и, пробив доску, вылетает со скоростью V₂ = 400 м/с. Найти среднюю силу сопротивления движению пули в доске.