Средняя квадратическая. Взаимосвязь степенных срених величин
Средняя квадратическая – простая и взвешенная.
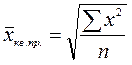 (4.13)
(4.13)
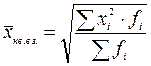 (4.14)
(4.14)
Пример: имеются 3 земельных участка в форме квадрата со сторонами:
X1= 100 м;
Х2= 200 м;
Х3= 300 м.
Определить среднюю величину стороны земельных участков. Если примем формулу средней арифметической, то получим, что общая площадь всех участков составляет 120 000 м2, что не соответствует действительности (реальная площадь 3-х участков равна 140 000 м2:
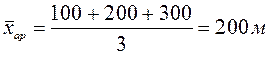
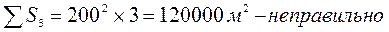 ,
,
т.к :
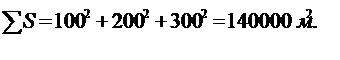
Для правильного расчета следует использовать формулу средней квадратической простой:
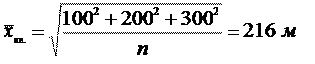
Все рассмотренные средние величины (кроме средней хронологической) являются степенными средними и выводятся из следующей общей формулы:
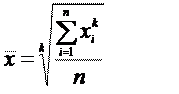 (4.15)
(4.15)
где при: k = –1 – получается средняя гармоническая;
k = 0 – средняя геометрическая;
k = 1 – средняя арифметическая;
k = 2 – средняя квадратическая;
k = 3 – средняя кубическая.
Все эти показатели рассчитываются для варьирующего признака для простых средних. Если все значения признака в ряде распределения одинаковы, то все значения средних равны. Между указанными средними величинами имеет место следующая зависимость (для одного ряда распределения):
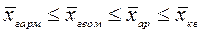 (4.16)
(4.16)
Мода и медиана
Мода – это наиболее часто встречающаяся варианта распределения или варианта, имеющая наибольшую частоту.
Для дискретных радов мода определяется визуально.
Пример: определить моду следующего ряда распределения.
Таблица 4.10 – Данные о проданных парах обуви, ед.
| Размер обуви (х) | Число проданных пар (f) | Накопленные частоты (cum f) |
| 12 (2 + 10) | ||
| 32 (12 + 20) | ||
| 37 | 88 | 120 (32 + 88) |
| 139 (120 + 19) | ||
| 148 (139 + 9) | ||
| 150 (148 + 2) | ||
| Итого | 150 | – |
Модой является размер 37, т.е. наибольшее число проданной обуви было 37-го размера.
Мода интервального ряда определяется по следующей формуле:
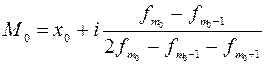 (4.17)
(4.17)
где: х0 – нижняя граница модального интервала;
i – величина модального интервала;
fm0– частота модального интервала;
fm0-1– частота интервала, предшествующего модальному;
fm0+1– частота интервала, следующего за модальным.
Модальный интервал – это интервал, имеющий наибольшую частоту.
Пример: определить моду следующего ряда распределения:
Таблица 4.12 Распределение работников предприятия по стажу в 2012 г.
| Стаж работы, лет (x) | Число работников (f) | Накопленные частоты (cum f) |
| до 2 2–4 4–6 6–8 8–10 свыше 10 | ||
| Итого | 100 | – |
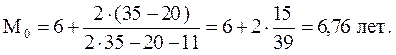
Ответ: наибольшее число работников имеет стаж работы 6,76 лет.
Медиана (Мe) – это варианта, которая приходится на середину ряда распределения, расположенного в порядке возрастания признаков. Она делит ряд распределения на 2 равные части.
Определение медианы для дискретного ряда распределения.
Медианой дискретного ряда является варианта, которая приходится на полусумму накопленных частот:
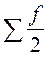 (4.18)
(4.18)
В нашем примере размер обуви 37 является также и медианой, т.е. половина проданной обуви меньше 37-го размера, другая половина – 37-го размера и больше.
Для интервального ряда Ме определяется по формуле:
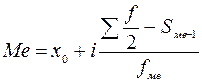 (4.19)
(4.19)
где х0– нижняя граница медианного интервала;
i – величина медианного интервала;
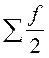 – полусумма накопленных частот;
– полусумма накопленных частот;
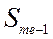 – сумма накопленных частот, интервалов, предшествующих медианному;
– сумма накопленных частот, интервалов, предшествующих медианному;
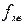 – частота медианного интервала.
– частота медианного интервала.
Медианный – это интервал, на который приходится полусумма накопленных частот. В нашем примере «6–8 лет» – медианный интервал.
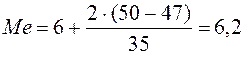
Это означает, что половина работников имеет стаж работы меньше 6,2 года, а другая половина больше.
Контрольные вопросы и задания
1. В чем заключается сущность статистической обработки методом средней величины?
2. Перечислите основные положения теории средних величин.
3. В каких случаях применяется средняя арифметическая простая? В чем ее отличие от средней арифметической взвешенной?
4. Какие свойства средних величин Вы знаете? Для чего они применяются?
5. Назовите виды средних степенных величин и напишите формулу степенной средней.
6. Какая зависимость существует между степенными средними величинами для одного ряда распределения?
7. Являются ли мода и медиана средними величинами и почему?
8. Как определить моду и медиану для дискретного ряда?
9. Что такое модальный и медианный интервалы? Могут ли они совпадать?
5. Изучение ВАРИАЦИи рядов распределения
Понятие вариации
Для каждой единицы изучаемой совокупности интересующий нас признак принимает различные значения, т.е. варьирует.
Вариация – это колебание признака в ряде распределения.
Рассмотрим 2 ряда чисел:
1) 75, 90, 78, 82, 93, 86 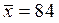
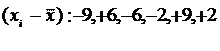
2) 65, 122, 84, 70, 105, 58 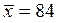
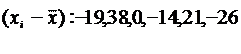
Разности следует освободить от знака для построения показателей вариации. Для этого нужно взять моду или четную степень. На этом принципе основано построение основных показателей вариации.
