Задания для выполнения расчетно-графической работы № 2
Методические указания и задания
К выполнению расчетно-графической работы № 2
Для всех направлений бакалавриата
Уфа 2012
00УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства протокол № ________ от ________________ 2010 г.
Составитель: доцент Дик Е.Н.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики доцент
Лукманов Р.Л.
Введение
Методические указания представили классическую форму самостоятельной деятельности в виде вариантов расчетно-графической работы, позволяющих осуществить индивидуальную проверку знаний студентов, а также способствующих приобретению ими устойчивых навыков в решении задач по указанной теме. Рассмотрены разделы векторной алгебры и аналитической геометрии на плоскости и в пространстве. В частности, выбраны задания по темам: скалярное, векторное и смешанное произведение векторов; определение уравнений линий первого и второго порядка; взаимное расположение прямой и плоскости; нахождение элементов пространственной фигуры. В настоящем сборнике представлены тридцать индивидуальных вариантов, каждый из которых содержит шесть заданий и примеры решения типовых задач. Варианты заданий выдаются преподавателем. Приводится библиографический список, рекомендуемый для дополнительного изучения, имеющийся в наличии в библиотеке БГАУ.
Представляем решение некоторых типовых заданий.
Задача 1. Найти косинус угла между векторами 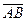 и
и 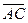 .
.
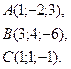
Решение.
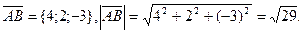


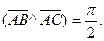
Задача 2.Показать, что x2 + y2 + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.
Решение.
Заданное уравнение преобразуем к виду (x - a)2 + (y - b)2 = r2. (1)
Выпишем члены, содержащие только x, и члены, содержащие только y. Выделим полные квадраты каждой переменной:
x2 + 4x = (x + 2)2 - 4,
y2 - 6y = (y - 3)2 - 9.
Левая часть уравнения запишется теперь так:
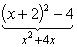
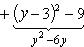
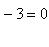
или отсюда
(x + 2)2 + (y - 3)2 = 16. (2)
Сравнивая уравнение (2) с (1), заключаем, что уравнение определяет окружность, центр которой имеет координаты О(-2, 3), r2 = 16, а r = 4.
Задача 3.Дана равносторонняя гипербола x2 - y2 = 8. Найти уравнение эллипса, фокусы которого находятся в фокусах гиперболы, если известно, что эллипс проходит через точку A(4, 6).
Решение.
Уравнение гиперболы преобразуем к каноническому виду и получим 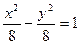 ,
, 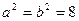 . Из соотношения
. Из соотношения 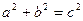 получаем, что c = 4. Значит, координаты фокусов гиперболы F2(-4, 0) и F1(4, 0). В этих точках находятся фокусы эллипса. Обозначим большую и малую полуоси эллипса через a1 и b1. Расстояние между фокусами эллипса такое же, как и расстояние между фокусами гиперболы. Поэтому половину этого расстояния по-прежнему обозначим через c. Но у эллипса
получаем, что c = 4. Значит, координаты фокусов гиперболы F2(-4, 0) и F1(4, 0). В этих точках находятся фокусы эллипса. Обозначим большую и малую полуоси эллипса через a1 и b1. Расстояние между фокусами эллипса такое же, как и расстояние между фокусами гиперболы. Поэтому половину этого расстояния по-прежнему обозначим через c. Но у эллипса
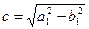
т. е. 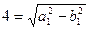 и
и 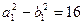 (1)
(1)
Для определения a1 и b1 нужно найти еще одно соотношение, связывающее их. Искомое уравнение эллипса запишется так:
 (2)
(2)
Поскольку точка A(4, 6) лежит на эллипсе, ее координаты должны удовлетворять уравнению эллипса. Подставляя в последнее уравнение x = 4, y = 6, получаем, что 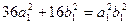 . Присоединяя уравнение (1) к этому уравнению, получаем для определения
. Присоединяя уравнение (1) к этому уравнению, получаем для определения 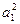 и
и 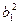 систему уравнений:
систему уравнений:
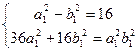
Откуда 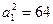 ;
; 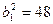 . Подставляя эти значения в (2), находим искомое уравнение
. Подставляя эти значения в (2), находим искомое уравнение 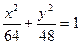 .
.
Задача 4. Вычислить площадь параллелограмма, построенного на векторах 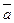 и
и  .
.
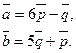

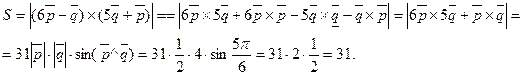
Задача 5. Вычислить объем тетраэдра с вершинами в точках  и его высоту, опущенную из вершины
и его высоту, опущенную из вершины  на грань
на грань 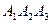 .
.
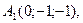


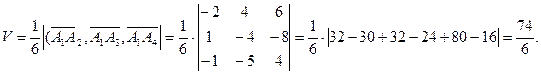

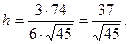
Задача 6.Найти расстояние от точки  до плоскости, проходящей через точки
до плоскости, проходящей через точки 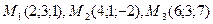 .
.
Уравнение плоскости, проходящей через 3 точки имеет вид:
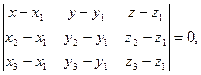
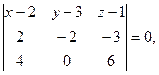


Задача 7.Найти точку 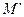 , симметричную точке
, симметричную точке 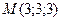 относительно прямой L, заданной уравнением
относительно прямой L, заданной уравнением 
Поместим прямую 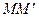 в некоторую плоскость α и составим ее уравнение
в некоторую плоскость α и составим ее уравнение 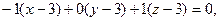 откуда
откуда 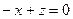 . Найдем точку пересечения прямой L и плоскости α.
. Найдем точку пересечения прямой L и плоскости α.
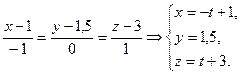
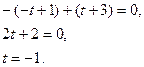
 - координаты точки пересечения.
- координаты точки пересечения.
Отсюда,

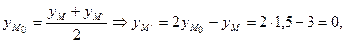

Следовательно,  - искомая точка.
- искомая точка.
Задания для выполнения расчетно-графической работы № 2
Задание № 1
1. Даны точки А(-2;3;-4), В(3;2;5), С(1;-1;2), D(3;2;-4). Вычислить 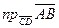 .
.
2. Даны точки М(-5;7;-6) и N(7;-9;9). Вычислить проекцию вектора 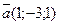 на ось вектора
на ось вектора 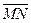 .
.
3. Сила, определяемая вектором 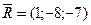 , разложена по трем направлениям, одно из которых задано вектором
, разложена по трем направлениям, одно из которых задано вектором 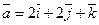 . Найти составляющую силы
. Найти составляющую силы 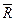 в направлении
в направлении  вектора
вектора 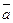 .
.
4. Даны векторы 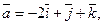
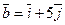 и
и 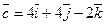 . Вычислить
. Вычислить 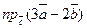 .
.
5. Даны векторы 
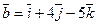 и
и  . Вычислить
. Вычислить 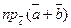 .
.
6. Вычислить проекцию вектора 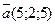 на ось вектора
на ось вектора 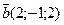 .
.
7. Даны точки A(3;-4;-2), B(2;5;-2). Найти проекцию вектора 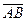 на ось, составляющую с координатными осями OX, OY углы
на ось, составляющую с координатными осями OX, OY углы  ,
,  , а с осью OZ – тупой угол
, а с осью OZ – тупой угол 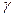 .
.
8. Найти проекцию вектора  на ось, составляющую с координатными осями OX, OZ углы
на ось, составляющую с координатными осями OX, OZ углы 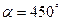 ,
, 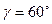 . А осью OY – острый угол
. А осью OY – острый угол 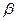 .
.
9. Найти проекцию вектора  на ось, составляющую с координатными осями равные острые углы.
на ось, составляющую с координатными осями равные острые углы.
10. Даны векторы 
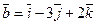 и
и 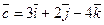 . Найти вектор
. Найти вектор  , удовлетворяющий условиям
, удовлетворяющий условиям 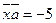 ,
, 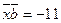 ,
,  .
.
11. Даны векторы 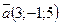 и
и  . Найти вектор
. Найти вектор  при условии, что он перпендикулярен к оси ОZ и удовлетворяет условиям
при условии, что он перпендикулярен к оси ОZ и удовлетворяет условиям 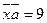 ,
, 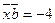 .
.
12. Найти вектор  , зная, что он перпендикулярен к векторам
, зная, что он перпендикулярен к векторам 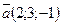 и
и 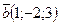 и удовлетворяет условию
и удовлетворяет условию  .
.
13. Вектор  , перпендикулярный к векторам
, перпендикулярный к векторам 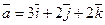 и
и 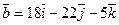 , образует с осью OY тупой угол. Найти его координаты, зная, что
, образует с осью OY тупой угол. Найти его координаты, зная, что 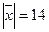 .
.
14. Найти вектор  , коллинеарный вектору
, коллинеарный вектору 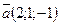 и удовлетворяющий условию
и удовлетворяющий условию 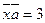 .
.
15. Вектор  , коллинеарный вектору
, коллинеарный вектору 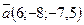 , образует острый угол с осью OZ. Зная, что
, образует острый угол с осью OZ. Зная, что 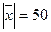 , найти его координаты.
, найти его координаты.
16. Вектор  перпендикулярен векторам
перпендикулярен векторам  и
и 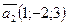 и удовлетворяет условию
и удовлетворяет условию  . Найти координаты
. Найти координаты  .
.
17. Даны векторы  и
и 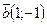 . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и 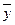 , удовлетворяющими системе уравнений
, удовлетворяющими системе уравнений 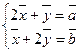 .
.
18. Векторы 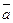 и
и 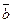 взаимно перпендикулярны; вектор
взаимно перпендикулярны; вектор 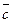 образует с ними углы, равные
образует с ними углы, равные 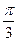 , зная, что
, зная, что 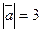 ,
, 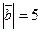 ,
,  , вычислить
, вычислить 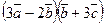 .
.
19. Вычислить длину диагоналей параллелограмма, построенного на векторах  и
и  если известно, что
если известно, что  ,
,  и
и 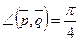 .
.
20. Проверить, являются ли точки A(-1;2;3), B(2;-1;1), C(1;-3;1) и D(-5;3;3) вершинами трапеции.
21. Определить при каком значении α векторы 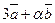 и
и 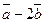 будут взаимно перпендикулярны, если
будут взаимно перпендикулярны, если  ,
,  ,
,  .
.
22. . Найти вектор  , образующий со всеми тремя базисными ортами острые углы, если
, образующий со всеми тремя базисными ортами острые углы, если 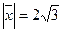 .
.
23. Найти угол, образованный единичными векторами 
 и
и 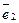 , если известно, что векторы
, если известно, что векторы 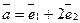 и
и  перпендикулярны.
перпендикулярны.
24. 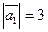 ,
, 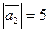 . Определить при каком значении
. Определить при каком значении 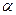 векторы
векторы 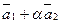 и
и 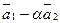 будут перпендикулярны.
будут перпендикулярны.
25. Доказать, что четырехугольник с вершинами А(-3;5;6), В(1;-5;7), С(8;-3;-1) и D(4;7;-2) – квадрат.
26. Найти длины сторон и величину угла треугольника с вершинами А(-1;-2;4), В(-4;-2;0), и С(3;-2; 1) при вершине С.
27. Вычислить работу силы 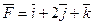 при перемещении материальной точки из положения А(-1;2;0) в положение В(2;1;3).
при перемещении материальной точки из положения А(-1;2;0) в положение В(2;1;3).
28. Зная, что 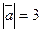 ,
,  ,
,  и
и 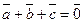 , вычислить
, вычислить 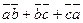 .
.
29. 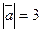 ,
,  ,
,  . Найти
. Найти 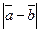 .
.
30. Найти cos  между диагоналями АС и BD параллелограмма, если заданы три его вершины А(2;1;3), В(5;2;-1), и С(-3;3; -3).
между диагоналями АС и BD параллелограмма, если заданы три его вершины А(2;1;3), В(5;2;-1), и С(-3;3; -3).
Задание № 2
По трем заданным точкам построить треугольник и средствами векторной алгебры найти: 1) длину стороны ВС; 2) уравнение линии ВС; 3) длину и уравнение высоты, проведенной из точки А; 4) площадь треугольника АВС; 5) угол между сторонами ВА и ВС; 6) уравнение биссектрисы, проведенной из вершины В; 7) составить уравнение медианы, проведенной из вершины С; 8) точку пересечения его медианы, проведенной из вершины С и высоты, проведенной из вершины А; 9) координаты точки М, делящей сторону АВ в отношении 2:3, считая от точки А; 10) уравнение прямой, проходящей через точку М параллельно стороне ВС. Координаты вершин треугольника даны в таблице.
| № варианта | А | В | С | № варианта | А | В | С |
| 5.1 | (-2; 5) | (4, 5) | (1, 1) | 5.16 | (6, 9) | (5, -4) | (4, 6) |
| 5.2 | (-3, 1) | (4, -5) | (7, 2) | 5.17 | (2, 3) | (4, 0) | (5, 3) |
| 5.3 | (4, -1) | (4, 4) | (6, 4) | 5.18 | (8, 7) | (3, 0) | (5, 6) |
| 5.4 | (-5, 3) | (4, 6) | (8, 4) | 5.19 | (8, 1) | (3, 0) | (3, 5) |
| 5.5 | (0, -6) | (3, 5) | (-2, 4) | 5.20 | (1, 3) | (7, 10) | (3, 2) |
| 5.6 | (-2, -3) | (10, 6) | (5, 2) | 5.21 | (4, 0) | (6, 9) | (-2, 1) |
| 5.7 | (-6, 2) | (1, 8) | (4, 5) | 5.22 | (-2, 1) | (-2, 5) | (4, 0) |
| 5.8 | (1, 5) | (6, 5) | (5, 7) | 5.23 | (-2, 1) | (-3, 1) | (4, 10) |
| 5.9 | (5, -2) | (7, 2) | (5, 5) | 5.24 | (1, -2) | (4, -1) | (6, 9) |
| 5.10 | (5, -2) | (8, 4) | (6, 5) | 5.25 | (3, 1) | (3, 2) | (1, 2) |
| 5.11 | (9, 6) | (2, 3) | (4, 0) | 5.26 | (1, -1) | (0, 4) | (1, -1) |
| 5.12 | (7, 5) | (4, 0) | (1, 2) | 5.27 | (1, -1) | (2, -3) | (4, 5) |
| 5.13 | (4, 7) | (3, 2) | (-7, 4) | 5.28 | (-2, 0) | (-1, 2) | (3, 4) |
| 5.14 | (7, 3) | (0, 6) | (6, 8) | 5.29 | (3, 2) | (1, 2) | (6, 6) |
| 5.15 | (4, 9) | (2, 4) | (5, 7) | 5.30 | (0, 4) | (-2, -4) | (6, 6) |
Задание № 3
1.Даны две смежные вершины А(-3;1) и В(2;2) параллелограмма АВСD и точка Q(3;0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.
2. Даны уравнения двух смежных сторон параллелограмма х-у-1=0, х-2у=0 и точка пересечения его диагоналей О(3;-1). Написать уравнения двух других сторон параллелограмма.
3. Какой угол образует с осью Ох прямая, проходящая через точку D(1;3) и точку пересечения медиан треугольника с вершинами А(-1;4),В(2;3), С(5;8)?
4. Известны вершины треугольника А(-4;-2),В(0;1), С(2;-1). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершины А, с высотой, проведенной из вершины В.
5. Известны уравнения прямых, на которых лежат две стороны ромба:
х+2у-4=0, х+2у-10=0 и уравнение одной из его диагоналей х-у+2=0. Найти координаты вершин ромба.
6. Дан треугольник с вершинами в точках А(1;-2),В(0;5), С(-6;5). Найти координаты центра описанной около треугольника окружности.
7. Составить уравнение прямой, симметричной прямой х+2у-6=0 относительно точки А(4;2).
8. Две смежные вершины квадрата имеют координаты (1;4) и (4;5). Найти координаты двух других вершин.
9. При каком значении 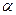 прямая х+у-
прямая х+у- 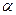 =0 касается окружности
=0 касается окружности 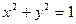 ?
?
10. Написать уравнение прямой, проходящей через точку А(2;5) на расстоянии 2 единиц от точки В(0;-1).
11. На прямой х-3у+8=0 найти координаты точки, равноудаленной от двух точек (5;4) и (-3;2).
12. Найти координаты основания перпендикуляра, опущенного из точки
А(-1;2) на прямую 3х-5у-21=0.
13. Дан треугольник с вершинами в точках А(2;5), В(5;-1), С(8;3). Составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х+у+4=0.
14. Через точку пересечения прямых 3х+2у-4=0 и х-5у+8=0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.
15. Дан четырехугольник ABCD с вершинами А(3;5),В(6;6), С(5;3), D(1;1). Найти: а) координаты точки пересечения диагоналей; б) угол между диагоналями.
16. Найти геометрическое место точек, отношение расстояний которых от двух данных точек А и В постоянно и равно 2.
17. Составить уравнение прямой, которая проходит через начало координат и вместе с прямыми х-у+12=0, 2х+у+9=0 образует треугольник с площадью, равной 1,5.
18. Составить уравнение прямой, проходящей через точку С(-5;4), зная , что длина ее отрезка, заключенного между прямыми х+2у+1=0 и х+2у-1=0, равна 5.
19. Составить уравнение прямой, которая проходит через точку С(1;1) и отсекает от координатного угла треугольник с площадью, равной 2.
20. Через точку М(4;3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Определить точки пересечения этой прямой с осями координат.
21. Составить уравнение прямой, проходящей через точку пересечения прямых 2х+7у-8=0, 3х+2у+5=0 под углом 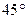 к прямой 2х+3у-7=0.
к прямой 2х+3у-7=0.
22. Составить уравнение прямой, которая проходит через точку пересечения прямых 11х+3у-7=0, 12х+у-19=0 на одинаковых расстояниях от точек А(3;-2) и В(-1;6).
23. Найти проекцию точки Р(-8;12) на прямую, проходящую через точки А(2;-3) и В(-5;1).
24. Найти точку М, симметричную точке Р(8;-9) относительно прямой, проходящей через точки А(3;-4) и В(-1;-2).
25. Точка А(-4;5) является вершиной квадрата, диагональ которого лежит на прямой 7х-у+8=0. Составить уравнения сторон и второй диагонали этого квадрата.
26. Даны две противоположные вершины квадрата А(-1;3) и С(6;2). Составить уравнения его сторон.
27. Луч света направлен по прямой х-2у+5=0. Дойдя до прямой 3х-2у+7=0, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
28. Даны две вершины треугольника А(-10;2) и В(6;4); его высоты пересекаются в точке Р(5;2). Определить координаты третьей вершины.
29. Составить уравнение прямой, проходящей через начало координат, зная , что длина ее отрезка, заключенного между прямыми 2х-у+5=0 и 2х-у+10=0, равна  .
.
30. Составить уравнение геометрического места точек, равноудаленных от двух прямых 3х-у+7=0 и 3х-у-3=0.
Задание № 4
1. Найти точки пересечения асимптот гиперболы x2-3у2=12 с окружностью, имеющей центр в правом фокусе гиперболы, и, проходящей через начало координат.
2. Написать уравнение прямой, проходящей через центры окружностей
х2+у2-6х-8у+16=0 и х2+у2+10х+4у+13=0.
3. Найти уравнение общей хорды окружностей (х-1)2+(у-3)2=4 и х2+у2-6х-10у+30=0.
4. Найти центр и радиус окружности, описанной около треугольника с вершинами А(0;2), В(1;1), С(2;-2).
5. Найти угол между радиусами окружности (х-4)2+(у+3)2=25, проведенными в точках ее пересечения с осью Ох.
6. Найти координаты точек эллипса 16х2+25у2-400=0, для которых расстояние от левого фокуса в три раза больше расстояния от правого фокуса.
7. Найти длину хорды эллипса 44х2+100у2=4400, направленной по диагонали прямоугольника, построенного на осях эллипса.
8. В эллипс 4х2+у2=4 вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной эллипса. Найти координаты двух других вершин треугольника.
9. Вывести уравнение геометрического места точек, для которых расстояние до данной точки А(3;0) равно расстоянию до данной прямой х+3=0.
10 Найти уравнения касательных к эллипсу х2+2у2=3, параллельных прямой х-2у+1=0
11. Найти уравнения касательных к гиперболе 4х2-5у2=20, параллельных прямой х+у-4=0.
12. Вершины квадрата лежат на гиперболе 9х2-4у2=125. Найти его площадь.
13. Найти расстояние между точками пересечения асимптот гиперболы
9х2-16у2=144 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.
14. На гиперболе х2-у2=1 найти точку, фокальные радиусы которой перпендикулярны.
15. Через левый фокус гиперболы х2-у2=8 проведен перпендикуляр к ее оси, содержащей вершины. Найти расстояния от фокусов до точек пересечения этого перпендикуляра с гиперболой.
16. При каких значениях 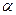 прямая у=2х+
прямая у=2х+ 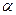 пересекает гиперболу
пересекает гиперболу
18х2-7у2=126? Касается ее?
17. Фокусы гиперболы совпадают с фокусами эллипса 9х2+25у2=225. Найти уравнение гиперболы, если ее эксцентриситет равен 2.
18. Найти уравнение гиперболы, симметричной относительно осей координат и касающейся прямой х-у-2=0 в точке М(4;2).
19. В параболу у2=12х вписан равносторонний треугольник, одна из вершин которого совпадает с вершиной параболы. Найти длину стороны треугольника.
20. Парабола у2=х отсекает от прямой, проходящей через начало координат, хорду, длина которой равна  . Составить уравнение этой прямой.
. Составить уравнение этой прямой.
21. Составить уравнение параболы с вершиной в начале координат, фокус которой находится в точке пересечения прямой 5х-3у+12=0 с осью ординат; осью абсцисс.
22. Составить уравнение параболы, симметричной относительно оси Оу и проходящей через точку пересечения прямой у-х=0 и окружности х2+у2-4у=0.
23. Дан эллипс 6х2+15у2=90. Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы в вершинах данного эллипса.
24. Найти длину диаметра эллипса (хорды, проходящей через центр эллипса)
9х2+27у2=225, перпендикулярно к асимптоте гиперболы х2-у2=4, проходящей через первую и третью четверти.
25. Чему равна площадь треугольника, образованного асимптотами гиперболы х2-у2=1 и прямой х=2.
26. Чему равна длина хорды, проходящей через фокус параболы х2=8у и перпендикулярной к ее оси симметрии.
27. Вычислить полуоси гиперболы, зная, что директрисы даны уравнениями
х = 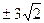 и угол между асимптотами прямой.
и угол между асимптотами прямой.
28. Составить уравнение прямой, которая касается параболы х2=16у и перпендикулярна к прямой 2х+4у+7=0
29. Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса 64х2+100у2=6400, а директрисы проходят через фокусы этого эллипса.
30. Фокусы гиперболы совпадают с фокусами эллипса 9х2+25у2=225. Составить уравнение гиперболы, если ее эксцентриситет 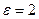
Задание № 5
Даны координаты четырех точек A,B,C,D.
1) написать уравнение плоскости 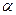 , проходящей через точку А перпендикулярно прямой ВС;
, проходящей через точку А перпендикулярно прямой ВС;
2) написать уравнение плоскости 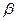 , проходящей через точки А, В, С;
, проходящей через точки А, В, С;
3) найти угол между плоскостями 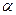 и
и 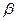 ;
;
4) найти уравнение и длину высоты, опущенной на грань АВС;
5) найти координаты точки, симметричной точке D относительно плоскости 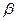 ;
;
6) найти площадь грани АВС;
7) найти объем пирамиды АВСD;
8) найти угол между ребрами АВ и АС.
1. А(7;2;4), В(7;-1;-2), С(3;3;1), D(-4;2;1).
2. А(1;3;6), В(2;2;1), С(-1;0;1), D(-4;6;-3).
3. А(-2;0;-4), В(-1;7;1), С(4;-8;-4), D(1;-4;6).
4. А(1;2;0), В(3;0;-3), С(5;2;6), D(8;4;-9).
5. А(1;3;6), В(2;2;1), С(-1;0;1), D(-4;6;-3).
6. А(-4;2; 6), В( 2;-3;0), С(-10;5;8), D( -5;2;-4).
7. А(7;2;4), В(7;-1;-2), С(3;3;1), D(-4;2;1).
8. А(2;1; 4), В(-1;5;-2), С(-7;-3;2), D(-6;-3;6).
9. А(-1;-5;2), В(-6;0;-3), С(3;6;-3), D(-10;6;7).
10. А(4;2;5), В(0;7;2), С(0;2;7), D(1;5;0).
11. А(4;4;10), В(4;10;2), С(2;8;4), D(9;6;9).
12. А(4;6;5), В(6;9;4), С(2;10;10), D(7;5;9).
13. А(3;5;4), В(8;7;4), С(5;10;4), D(4;7;8).
14. А(10;6;6), В(-2;8;2), С(6;8;9), D(7;10;3).
15. А (1;8;2), В(5;2;6), С(5;7;4), D(4;10;9).
16. А(6;6;5), В(4;9;5), С(4;6;11), D(6;9;3).
17. А(7;2;2), В(5;7;7), С(5;3;1), D(2;3;7).
18. А(8;6;4), В(10;5;5), С(5;6;8), D(8;10;7).
19. А(7;7;3), В(6;5;8), С(3;5;8), D(8;4;1).
20. А(-1;2;7), В(-1;5;1), С(1;2;1), D(1;5;9).
21. А(4;2;5), В(0;7;2), С(0;2;7), D(1;5;0).
22. А(7;2;4), В(7;-1;-2), С(3;3;1), D(-4;2;1).
23. А(-1;2;7), В(-1;5;1), С(1;2;1), D(1;5;9).
24. А(7;2;2), В(5;7;7), С(5;3;1), D(2;3;7).
25. А(1;1;1), В(4;4;4), С(3;5;5), D(2;4;7).
26. А(8;7;4), В(3;5;4), С(5;10;4), D(4;7;8).
27. А(1;2;7), В(-2;3;5), С(2;3;6), D(8;4;1).
28. А(5;3;4), В(-1;4;2), С(0;3;6), D(4;5;9).
29. А(2;2;5), В(2;-3;5), С(0;1;2), D(2;3;4).
30. А(2;1;4), В(7;-1;-2), С(-7;-3;2), D(-4;2;1).
Задание № 6
1. При каком значении m прямая 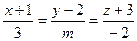 параллельна плоскости
параллельна плоскости 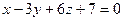 ?
?
2. Составить уравнение плоскости, проходящей через т. 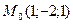 перпендикулярно к прямой
перпендикулярно к прямой  .
.
3. При каком значении С прямая 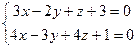 параллельна плоскости
параллельна плоскости 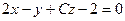 ?
?
4. При каких значениях A и D прямая 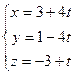 лежит в плоскости
лежит в плоскости  ?
?
5. При каких значениях A и B плоскость  перпендикулярна к прямой
перпендикулярна к прямой 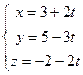 ?
?
6. Убедившись, что прямые 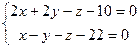 ;
; 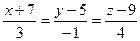 параллельны, вычислить расстояние d между ними.
параллельны, вычислить расстояние d между ними.
7. Вычислить расстояние d от точки P(2;3;-1) до прямой 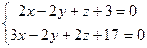 .
.
8. Составить уравнение плоскости, проходящей через две параллельные прямые  ;
; 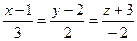 .
.
9. Доказать, что прямые  ;
;  лежат в одной плоскости, и составить уравнение этой плоскости.
лежат в одной плоскости, и составить уравнение этой плоскости.
10. Вычислить кратчайшее расстояние между двумя прямыми: 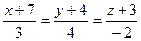 ;
; 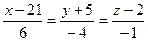 .
.
11. Вычислить кратчайшее расстояние между двумя прямыми:  ;
;  .
.
12. Вычислить кратчайшее расстояние между двумя прямыми: 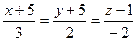 ;
;  .
.
13. Найти точку Q симметричную т. P (1,3,-4) относительно плоскости 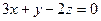 .
.
14. Составить уравнение плоскости, проходящей через т. N (1,1,1) перпендикулярно к прямой 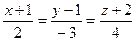 . Найти их точку пересечения.
. Найти их точку пересечения.
15. Найти проекцию точки A (4,-3,1) на плоскость 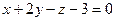 .
.
16. Найти проекцию точки P (2,-1,3) на прямую 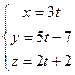 .
.
17. Найти уравнение плоскости, проходящей через параллельные прямые 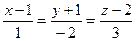 ;
;  .
.
18. Даны прямые 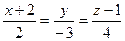 и
и  . При каком
. При каком  они пересекаются?
они пересекаются?
19. Написать уравнение прямой, проходящей через т. (1,-1,0) и перпендикулярной к плоскости  .
.
20. Найти расстояние между параллельными плоскостями  и
и 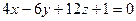 .
.
21. Найти проекцию прямой  на плоскость OXY.
на плоскость OXY.
22. Через точки 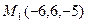 и
и 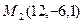 проведена прямая. Определить точку переcечения этой прямой с координатной плоскостью YOZ.
проведена прямая. Определить точку переcечения этой прямой с координатной плоскостью YOZ.
23. Составить уравнение прямой, проходящей через т. A(3,-3,0) и через точку пересечения прямой  :
:  с плоскостью α, заданной уравнением
с плоскостью α, заданной уравнением 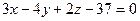 .
.
24. Составить уравнение прямой, проходящей через т. A(2,-1,3) и через точку пересечения прямой  :
:  с плоскостью α, заданной уравнением
с плоскостью α, заданной уравнением  .
.
25. Написать общее уравнение плоскости, проходящей через пересекающиеся прямые  :
: 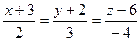 и
и 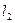 :
:  .
.
26. Написать общее уравнение плоскости, проходящей через точку М (1;2;1) параллельно прямым  :
:  и
и 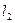 :
: 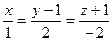 .
.
27. Написать общее уравнение плоскости, проходящей через прямую  :
: 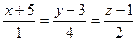 параллельно прямой
параллельно прямой 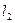 :
: 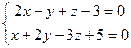 .
.
28. Составить каноническое уравнение прямой, заданной как линия пересечения двух плоскостей:  и
и 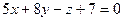 .
.
29. Составить уравнения прямой, проходящей через точки пересечения плоскости:  с прямыми:
с прямыми: 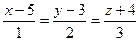 и
и  .
.
30. Найти точку, симметричную точке А (4;-3:2) относительно прямой  :
: 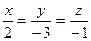 .
.
Библиографический список
1. Шипачев В. С. Высшая математика: учебник для студ. вузов/ В. С. Шипачев. - Изд. 8-е, стер. - М.: Высшая школа, 2007. - 479с.
2. Сборник задач по высшей математике: с контрольными работами. 1 курс: учеб. пособие для студ. вузов, обуч. по направлениям и спец. в области техники и технологии/ К. Н. Лунгу и др. - 6-е изд.. - М.: Айрис Пресс, 2007. - 575с.
3. Данко П. Е.Высшая математика в упражнениях и задачах: учеб. пособие: в 2 ч./ П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. Ч. 1- 6-е изд. - М.: ОНИКС: Мир и Образование. - 2006. – 304с.
4. Кузнецов Л. А. Сборник заданий по высшей математике. Типовые расчеты: учеб. пособие/ Л. А. Кузнецов. - Изд. 10-е, стер. - СПб.; М.; Краснодар: Лань, 2008. - 239с.
