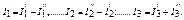Метод преобразования схемы

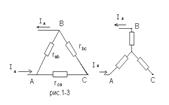
Условия эквивалентности звезды и треугольника проще всего определяются посредством сопоставления межузловых сопротивлений и проводимостей двух этих схем. Возьмем некоторый источник напряжения и присоединим к нему сначала узлы А и В треугольника (рис.1-3), затем – одноименные узлы звезды. В случае эквивалентности треугольника и звезды в обоих случаях сила тока I_a, которой будет нагружен источник, должна быть одинакова, что будет иметь место, если одинаковы проводимости, а следовательно, и сопротивления между узлами А и В треугольника и звезды. Это равенство сопротивлений должно иметь место также при включении к источнику энергии узлов В и С, а затем и узлов С и А.

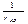Проводимость между узлами А и В треугольника складывается из проводимости стороны А – В, равной , и проводимости, образуемой соединенными последовательно по отношению к узлам А, В сторон ВС и СА. Эта проводимость будет 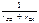. Следовательно, общая проводимость между узлами А и В треугольника равна:

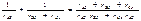
Сопротивление между узлами А, В треугольника – величина, обратная проводимости между этими узлами, т.е. оно равно:

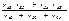
При соединении звездой сопротивление между теми же узлами А, В будет равно сумме сопротивлений двух соответствующих лучей звезды, т.е. оно будет равно .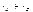

Согласно условию эквивалентности должно иметь место равенство

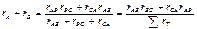(3-1)

здесь 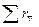-- сумма сопротивлений всех трех сторон треугольника.

Структура схем звезды и треугольника по отношению к узлам симметрична, поэтому уравнения равенства сопротивлений для узлов В, С, а затем и для узлов С, А можно получить из (3-1) путем простой циклической перестановки индексов:

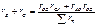(3-2)

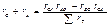(3-3)

Чтобы определить 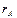, сложим (3-1) и (3-3) и вычтем из этой суммы (3-2); разделив последнюю на 2, найдем:

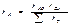(3-4)

Два остальных уравнения получим путем простой циклической перестановки индексов в правой части:

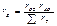(3-5)

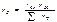(3-6)

При некоторых расчетах целесообразно осуществить обратное преобразование звезды в эквивалентный треугольник. Чтобы составить уравнения для такого преобразования, перемножим попарно выражения (3-4), (3-5), (3-6) и, сложив полученные произведения, получим:

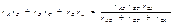
затем последнее выражение разделим на (3-6) и таким путем определим:

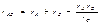(3-7)

после чего посредством циклической перестановки индексов найдем выражения сопротивлений остальных двух сторон эквивалентного треугольника:

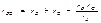(3-8)

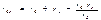(3-9)

МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Метод основан на применении первого закона Кирхгофа и заключается в следующем:

1) один узел схемы цепи принимаем базисным с нулевым потенциалом. Такое допущение не изменяет значения токов в ветвях, так как ток в каждой ветви зависит только от разностей потенциалов узлов, а не от действительных значений потенциалов;

2) для остальных узлов составляем уравнения по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов;

3) решением составленной системы уравнений определяем потенциалы узлов относительно базисного, а затем токи ветвей по обобщенному закону Ома.

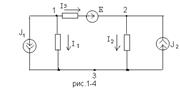
Узел 3 принимаем базисным, т.е. 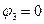. Для узлов 1 и 2 уравнения по первому закону Кирхгофа:

узел 1 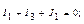узел 2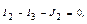

где 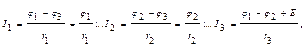после подстановки

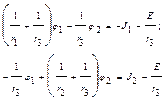(4-1)

Решение системы уравнений (4-1) методом подстановок определяет потенциалы узлов, а следовательно, и токи ветвей.

В частном случае схемы замещения без источников тока с двумя узлами потенциал узла 1 при базисном узле 2, т.е. при 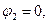равен напряжению между узлами

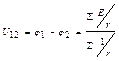(4-2)

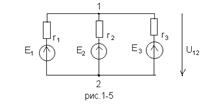
Выражение (4-2) называется формулой межузлового напряжения. Например, для цепи на схеме рис.1-5 напряжение между узлами по (4-2)

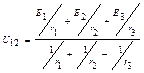
МЕТОД КОНТУРНЫХ ТОКОВ

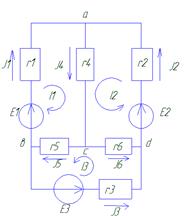
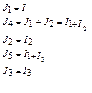
Для расчета по методу контурных токов схема сложной цепи по кратчайшим путям разбивается на отдельные контуры-ячейки. Затем в каждом из контуров произвольно выбирается направление контурного тока, т.е. тока, замыкающего только в данном контуре. Токи в ветвях, являющимися общими для двух или более контуров, определяются на основании первого закона Кирхгофа как алгебраическая сумма соответствующих контурных токов. Благодаря такой подстановке соответственно уменьшается число рассчитываемых токов, а уравнения схемы составляются на основании только второго закона Кирхгофа, причем направление обхода контуров берется совпадающим с направлением контурных токов.

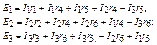
ПРИНЦИП И МЕТОД НАЛОЖЕНИЯ

На принципе наложения основан расчет цепей по методу наложения. Согласно этому методу при расчете схемы, содержащей несколько источников э.д.с., поочередно полагаются равными нулю все э.д.с., кроме одной. Производится расчет токов в схеме, создаваемых действием одной этой э.д.с. Расчет производится отдельно для каждой из э.д.с., содержащейся в схеме. Действительные значения токов в отдельных ветвях схемы определяются посредством алгебраического сложения токов, создаваемых независимым действием отдельных э.д.с.

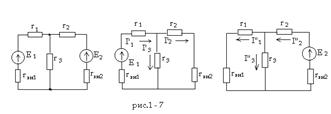
Сначала исключается э.д.с. E₂, но на месте ее источника в схеме сохраняется внутреннее сопротивление r_вн2 (если его нужно учитывать). После исключения E₂ схема представляет собой простое смешанное соединение, поэтому ток в ее неразветвленной части будет:

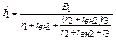а токи в двух ветвях схемы будут:

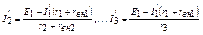
Затем в схеме исключается E₁ и, при наличии только э.д.с. E₂, рассчитываются токи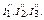

Токи в схеме, при наличии всех источников э.д.с., будут: