Перерезывающие силы и изгибающие моменты при изгибе балок
Согласно гипотезе плоских сечений (см. п. 1.5) плоские поперечные сечения балки до деформации остаются плоскими и после деформации. При изгибе эти плоские сечения взаимно поворачиваются одно относительно другого. Очевидно, такой поворот происходит вследствие растяжения одних волокон материала и сжатия других. В нашем примере на рис. 8.1, б верхние волокна (на вогнутой стороне балки) сжимаются, а нижние – растягиваются. Отсюда можно сделать заключение, что у балки имеется такой слой волокон, который не испытывает ни растяжения. ни сжатия. Этот слой называется нейтральным слоем. Линия пересечения нейтрального слоя с плоскостью какого-либо поперечного сечения называется нейтральной осью (совпадает с упругой линией балки, пунктир на рис. 8.1,б). Таким образом, верхняя и нижняя стороны сечения при изгибе искривятся по-разному: нижняя часть сечения удлинится, а верхняя – укоротится (см. рис. 8.1, б).
Эти весьма ценные и, казалось бы, простые выводы не сразу были сделаны учеными. Потребовалось около столетия со времени начала изучения изгиба, чтобы прийти к правильному пониманию этого явления. Галилей, положивший начало создания научной теории изгиба, еще в начале XVIII века сделал неправильное предположение, что при изгибе все волокна материала одинаково удлиняются. И только в конце XVIII столетия опытным путем было установлено, что при изгибе одни волокна (на выпуклой стороне) растягиваются, а другие (на вогнутой стороне) сжимаются.
Вследствие удлинения одних волокон и укорочения других в балке возникает один из внутренних силовых факторов – изгибающий момент. Кроме этого, как было установлено, при изгибе балки одни сечения балки сдвигаются по отношению к другим (русский ученый, инженер Д.И. Журавский), что приводит к другому внутреннему силовому фактору – перерезывающей (поперечной) силе.
Изгибающий момент – это главный момент всех нормальных к сечению балки элементарных внутренних сил относительно нейтральной оси, которая совпадает с главной центральной осью поперечного сечения:
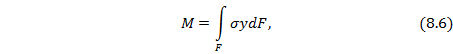
где σ – нормальные напряжения, перпендикулярные к плоскости поперечного сечения.
Изгибающий момент численно равен алгебраической сумме моментов всех сил (включая реакции), расположенных по одну сторону от сечения, относительно центра тяжести этого сечения.
Изгибающий момент положителен, если верхние волокна балки сжимаются (правило знаков, принятое в сопротивлении материалов) рис. 8.13, а.
Перерезывающая сила – это главный вектор всех внешних сил в сечении по направлению совпадающий с вертикальной главной осью поперечного сечения:
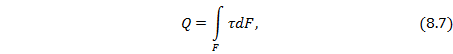
где 𝜏 – касательные напряжения, лежащие в плоскости поперечного сечения.
Перерезывающая сила численно равна алгебраической сумме проекций всех внешних сил (включая реакции), на вертикальную ось у, перпендикулярную оси балки.
Перерезывающая сила положительна, если она стремится вращать сечение левой отсеченной части балки по часовой стрелке, а в противоположном направлении для правой отсеченной части балки – отрицательна (рис. 8.13, б).
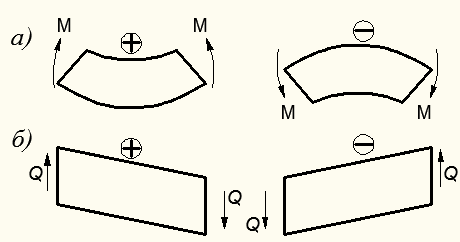
Рисунок 8.13 – Правило знаков для М и 
Графики изменения величин М и  по длине балки называются эпюрами. Эпюры строятся с учетом правил знаков М и
по длине балки называются эпюрами. Эпюры строятся с учетом правил знаков М и  по участкам балки. Здесь под участками эпюры подразумевается расстояние между концом балки и опорой, между опорой и внешними силовыми факторами и между самими силовыми факторами. Положительные ординаты эпюр М и
по участкам балки. Здесь под участками эпюры подразумевается расстояние между концом балки и опорой, между опорой и внешними силовыми факторами и между самими силовыми факторами. Положительные ординаты эпюр М и  откладываются вверх от оси балки (см. п. 8.2).
откладываются вверх от оси балки (см. п. 8.2).
Если на балку действует равномерно распределенная нагрузка интенсивностью q (см. рис. 8.6), то порядок построения эпюр М и  следующий:
следующий:
1. Определяем величины реакций RА и RВ из условий статики (см. п. 8.2): 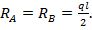
2. Строим эпюру  , пользуясь методом сечений по участку между опорами: в сечении х мысленно отбрасываем часть балки, например, левую. Действие отброшенной части балки на оставшуюся заменяем внутренней силой упругости – перерезывающей силой
, пользуясь методом сечений по участку между опорами: в сечении х мысленно отбрасываем часть балки, например, левую. Действие отброшенной части балки на оставшуюся заменяем внутренней силой упругости – перерезывающей силой  (х):
(х): 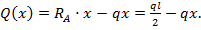
Рисунок 8.14 – Эпюры М и  для балки для балки |
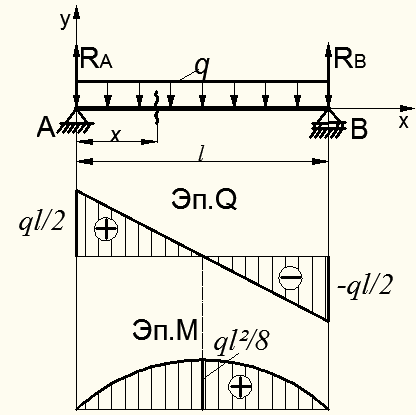 Из полученного выражения видим, что переменная х в первой степени, значит закон изменения усилия
Из полученного выражения видим, что переменная х в первой степени, значит закон изменения усилия 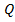 по участку соответствует прямой линии для крайних координат: при х=0
по участку соответствует прямой линии для крайних координат: при х=0 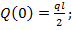 при
при 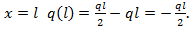 Соединяем крайние координаты эпюры прямой линией с указанием знаков
Соединяем крайние координаты эпюры прямой линией с указанием знаков  (см. эп.
(см. эп.  на рис. 8.14).
на рис. 8.14). 3. Строим эпюру М с использованием метода сечений. При рассмотрении мысленно отбрасываемой левой части балки имеем (с учетом принятых знаков для М) закон изменения М(х) по участку:
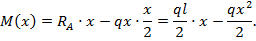
Полученное выражение содержит переменную х во второй степени. А это означает, что закон изменения М по участку балки соответствует квадратичной параболе: при 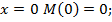 при
при 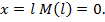
Максимум эпюры М на участке определим по условию существования экстремума:
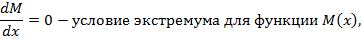
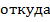
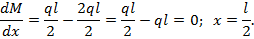
Т.е. максимум эпюры М будет при координате 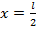 и соответствует значению
и соответствует значению 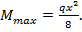 Максимальное значение
Максимальное значение  по абсолютной величине будет на опорах
по абсолютной величине будет на опорах 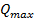 =
= 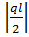 .
.
Отметим при этом, что максимум эпюры М имеет место в точке, где на эпюре  значение
значение  =0.
=0.
Таким образом, при согласовании эпюр  и М необходимо помнить, что на эпюрах, где
и М необходимо помнить, что на эпюрах, где 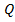 =0, имеет место Мmax.
=0, имеет место Мmax.
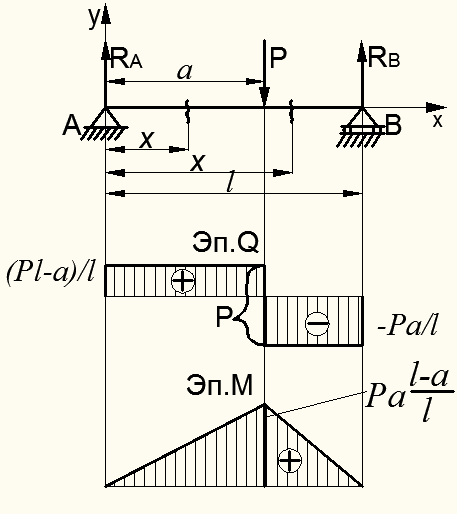
В другом типичном случае нагрузки балки сосредоточенной силой Р (см. рис. 8.7) построение эпюр  и М соответствует такой последовательности действий.
и М соответствует такой последовательности действий.
1. Определяем величину реакций RА и RВ из условий статики (см. п. 8.2): 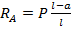 ;
; 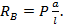
Рисунок 8.15 – Эпюры М и  для балки для балки |
 соответствует двум участкам балки:1-й участок при
соответствует двум участкам балки:1-й участок при 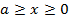 ; 2-й участок при
; 2-й участок при 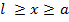 .
. Имеем на первом участке: 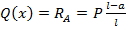 (ординаты соответствуют прямой линии): при
(ординаты соответствуют прямой линии): при 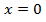 и
и 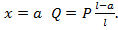
На участке закон изменения  соответствует прямой с ординатой
соответствует прямой с ординатой 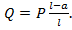
На втором участке закон изменения  соответствует зависимости:
соответствует зависимости:
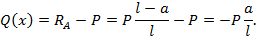
А это – прямая линия с ординатой 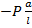 на этом участке (см.эп.
на этом участке (см.эп. 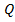 на рис. 8.15).
на рис. 8.15).
Обращаем внимание, что в месте действия сосредоточенной силы Р на балку имеет место имеет скачок на величину этой силы по эп. 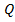 (см. рис. 8.15).
(см. рис. 8.15).
3. Переходим к построению эпюр М по участкам балки.
На 1-м участке: 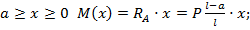 при
при  при
при 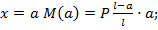 закон изменения изгибающего момента на участке – прямая линия (см. эп. М на рис. 8.15).
закон изменения изгибающего момента на участке – прямая линия (см. эп. М на рис. 8.15).
На 2-и участке: 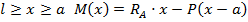 ; при
; при 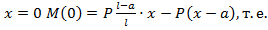 закон изменения эп. М на участке – прямая линия: при
закон изменения эп. М на участке – прямая линия: при 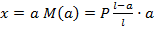 ,
, 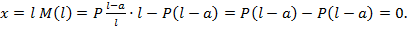 Показываем эп. М на рис. 8.15.
Показываем эп. М на рис. 8.15.
В итоге для балки: 
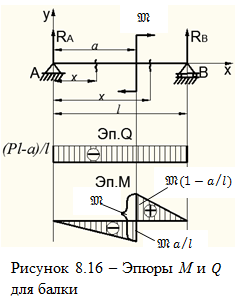
Еще один типичный случай нагрузки балки – это действие в пролете сосредоточенного внешнего момента 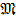 (рис.8.16). Покажем последовательность построения эпюр
(рис.8.16). Покажем последовательность построения эпюр  и М.
и М.
1. Определяем величины реакций на опорах балки: 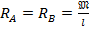 (см.п.8.2).
(см.п.8.2).
 |
 . На 1-м участке
. На 1-м участке 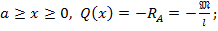 при
при 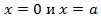 _
_ 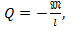 что соответствует прямой линии на участке.
что соответствует прямой линии на участке.
 На втором участке
На втором участке 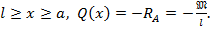
А это продолжение прямой линии 2-го участка (см. рис. 8.16).
3. Эпюра М на участках балки такая:
На 1-м участке
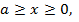
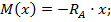
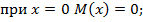
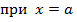
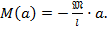
Эпюра М на этом участке соответствует прямой линии.
На 2-м участке при
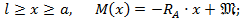
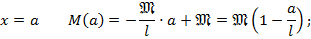
при 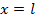 _
_ 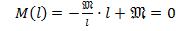 (см. рис. 8.16)
(см. рис. 8.16)
Обращаем внимание, что в месте приложения внешнего сосредоточенного момента 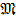 на эпюре М будет иметь место скачок на величину этого момента (см. рис. 8.16).
на эпюре М будет иметь место скачок на величину этого момента (см. рис. 8.16).
При построении эпюр  и М кроме рассмотренного аналитического способа существуют и другие подходы: построение эпюр по характерным точкам; способ сложения действия сил [1, 4, 12].
и М кроме рассмотренного аналитического способа существуют и другие подходы: построение эпюр по характерным точкам; способ сложения действия сил [1, 4, 12].
