Непрерывность функции в точке и на интервале

Непрерывность функции. Точки разрыва. Как исследовать функцию на непрерывность?

На данном уроке мы разберём понятие непрерывности функции, классификацию точек разрыва и распространённую практическую задачу исследования функции на непрерывность. Из самого названия темы многие интуитивно догадываются, о чём пойдёт речь, и думают, что материал довольно простой. Это правда. Но именно несложные задачи чаще всего наказывают за пренебрежение и поверхностный подход к их решению. Поэтому рекомендую очень внимательно изучить статью и уловить все тонкости и технические приёмы.

Что нужно знать и уметь?Не очень-то и много. Для качественного усвоения урока необходимо понимать, что такое предел функции. Читателям с низким уровнем подготовки достаточно осмыслить статью Пределы функций. Примеры решений и посмотреть геометрический смысл предела в методичке Графики и свойства элементарных функций. Также желательно ознакомиться с геометрическими преобразованиями графиков, поскольку практика в большинстве случаев предполагает построение чертежа. Перспективы оптимистичны для всех, и даже полный чайник сумеет самостоятельно справиться с задачей в ближайший час-другой!

Непрерывность функции. Точки разрыва и их классификация

Понятие непрерывности функции

Рассмотрим некоторую функцию 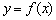, непрерывную на всей числовой прямой:

Или, говоря лаконичнее, наша функция непрерывна на 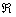(множестве действительных чисел).

Каков «обывательский» критерий непрерывности? Очевидно, что график непрерывной функции можно начертить, не отрывая карандаша от бумаги.

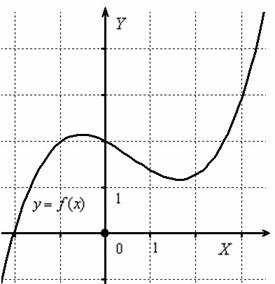
При этом следует чётко отличать два простых понятия: область определения функции и непрерывность функции. В общем случае это не одно и то же. Например:

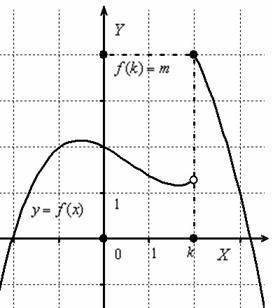
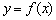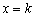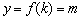Данная функция определена на всей числовой прямой, то есть для каждого значения «икс» существует своё значение «игрека» . В частности, если , то . Заметьте, что другая точка выколота, ведь по определению функции, значению аргумента должно соответствовать единственное значение функции. Таким образом, область определения нашей функции: .

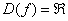Однако эта функция не является непрерывной на 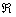! Совершенно очевидно, что в точке 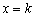она терпит разрыв. Термин тоже вполне вразумителен и нагляден, действительно, карандаш здесь по любому придётся оторвать от бумаги. Немного позже мы рассмотрим классификацию точек разрыва.

Непрерывность функции в точке и на интервале

В той или иной математической задаче речь может идти о непрерывности функции в точке, непрерывности функции на интервале, полуинтервале или непрерывности функции на отрезке. То есть, не существует «просто непрерывности» – функция может быть непрерывной ГДЕ-ТО. И основополагающим «кирпичиком» всего остального является непрерывность функции в точке.

Теория математического анализа даёт определение непрерывности функции в точке с помощью «дельта» и «эпсилон» окрестностей, но на практике в ходу другое определение, которому мы и уделим самое пристальное внимание.

Сначала вспомним односторонние пределы, ворвавшиеся в нашу жизнь на первом урокео графиках функций. Рассмотрим будничную ситуацию:

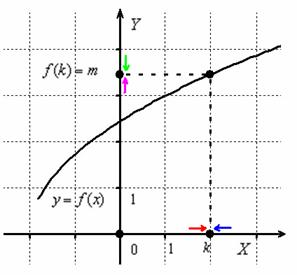
Если приближаться по оси 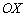к точке 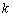слева (красная стрелка), то соответствующие значения «игреков» будут идти по оси 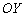к точке 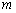(малиновая стрелка). Математически данный факт фиксируется с помощью левостороннего предела:

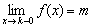
Обратите внимание на запись 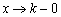(читается «икс стремится к ка слева»). «Добавка» «минус ноль» символизирует бесконечно малое отрицательное число, по сути это и обозначает, что мы подходим к числу 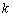с левой стороны.

Аналогично, если приближаться к точке «ка» справа (синяя стрелка), то «игреки» придут к тому же значению 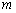, но уже по зелёной стрелке, и правосторонний предел оформится следующим образом:

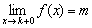
«Добавка» 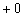символизирует бесконечно малое положительное число, и запись 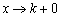читается так: «икс стремится к ка справа».

Если односторонние пределы конечны и равны (как в нашем случае): 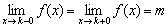, то будем говорить, что существует ОБЩИЙ предел 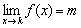. Всё просто, общий предел – это наш «обычный» предел функции, равный конечному числу.

Заметьте, что если функция не определена при 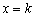(выколите чёрную точку на ветке графика), то перечисленные выкладки остаются справедливыми. Как уже неоднократно отмечалось, в частности, в статье о бесконечно малых функциях, выражения 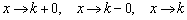означают, что «икс» бесконечно близко приближается к точке 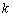, при этом НЕ ИМЕЕТ ЗНАЧЕНИЯ, определена ли сама функция в данной точке или нет. Хороший пример встретится в следующем параграфе, когда анализу подвергнется функция .

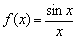Определение: функция непрерывна в точке , если предел функции в данной точке равен значению функции в этой точке: .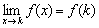

Определение детализируется в следующих условиях:

1) Функция должна быть определена в точке , то есть должно существовать значение .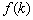

2) Должен существовать общий предел функции 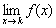. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: .

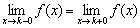3) Предел функции в данной точке должен быть равен значению функции в этой точке: 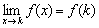.