Метод искусственного базиса

Метод искусственного базиса применяется для решения задач ЛП в случае, когда задача не имеет начального опорного решения с базисом из единичных векторов.

Пусть задана задача ЛП в канонической форме, то есть имеет вид (1.6), и в ней отсутствует единичный базис. К этой задаче строим вспомогательную задачу (ВЗ):

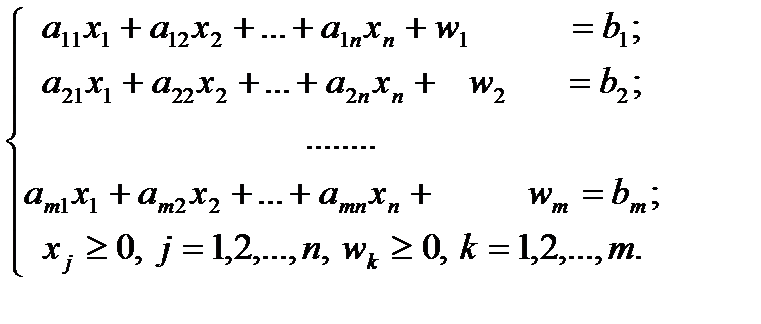
Здесь w₁, w₂,…, w_m – искусственные переменные. Запишем ограничения в векторном виде: A₁x₁+A₂x₂+…+A_nx_n+A_n+1w₁+…+A_n+mw_m =B, где 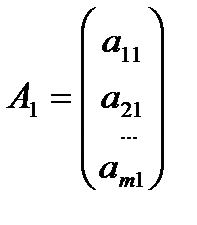, , 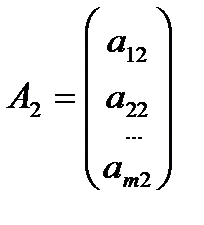…, , , , 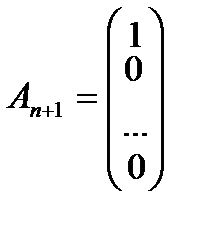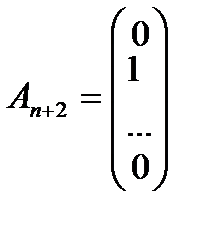…, , 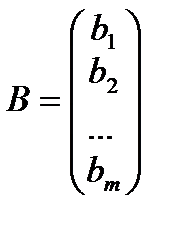. Таким образом, вектора 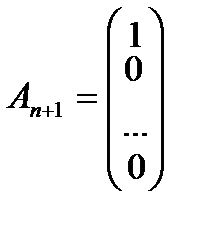, , 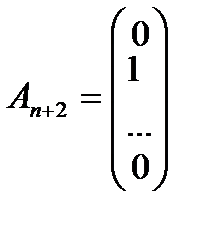…, образуют единичный базис в R^m, и все искусственные переменные соответствующие этим векторам будут базисными. Далее строится обычная симплекс-таблица. Если ВЗ не имеет решения в силу неограниченности целевой функции, то исходная задача также не имеет решения по той же причине. Пусть в результате знакомых по симплекс-методу необходимых преобразований получили оптимальную симплекс-таблицу к ВЗ. Очевидно, что максимальное значение целевой функции ВЗ равно 0, то есть max F=0. Если же maxF<0, то исходная задача ЛП не имеет решения в силу несовместности системы ограничений. Предположим, что max F=0. Тогда возможны такие ситуации:

1) все искусственные переменные стали свободными и были исключены из таблицы. В этом случае вычеркиваем столбцы, соответствующие искусственным переменным и последнюю строку. Вместо неё приписываем новую строку оценок, но с использованием исходной целевой функции Z(X). Тем самым получена начальная симплекс-таблица для исходной задачи ЛП, к которой применяем симплекс-метод;

2) в оптимальном решении ВЗ хотя бы одна искусственная переменная осталась базисной. Тогда:

а) либо все числа в строках, соответствующих оставшимся базисным искусственным переменным, равны 0;

б) либо есть хоть одно отличное от 0.

В первом случае, поступаем также как и пункте 1). Во втором, выбираем любой ненулевой элемент в качестве ведущего и делаем шаг жордановых исключений. Через конечное число шагов мы придем или к пункту 1), или к пункту 2)а).

Заметим, что если среди векторов A_j , j=1,2,…,n, были вектора, которые могли бы войти в базис, то искусственные переменные вводят только в те уравнения системы ограничений, в которых отсутствует базисная переменная.

Пример 1.3. Максимизировать функцию Z=x₁+2x₂-2x₃ при ограничениях

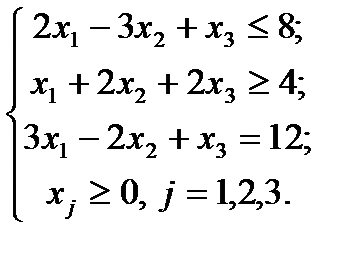
Решение. Преобразуем исходную задачу линейного программирования к канонической. Для этого введём в ограничения дополнительные неотрицательные переменные. А именно, в первое неравенство – переменную x₄ со знаком «+», во второе – x₅ со знаком «-» . Система ограничений примет вид:

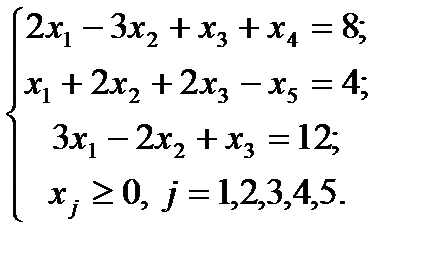
Эту систему запишем в векторной форме: A₁x₁+A₂x₂+A₃x₃+A₄x₄+A₅x₅=B, где

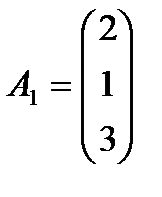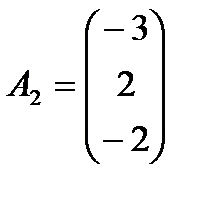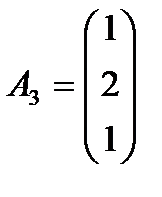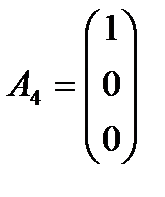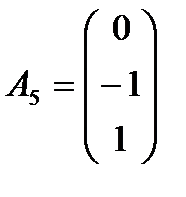, , , , , . Очевидно, что в данной системе ограничений отсутствует единичный базис. Это означает, что среди векторов A_j нет трёх необходимых единичных векторов, которые должны образовывать базис в R³. Однако заметим, что вектор A₄ является частью базиса. Ему соответствует базисная переменная x₄. Необходимо найти ещё два единичных вектора. Для этого применим метод искусственного базиса. Введём искусственные переменные в те уравнения ограничений, в которых не присутствует базисная переменная x₄ и построим следующую вспомогательную задачу (ВЗ):

F=-w₁-w₂®max

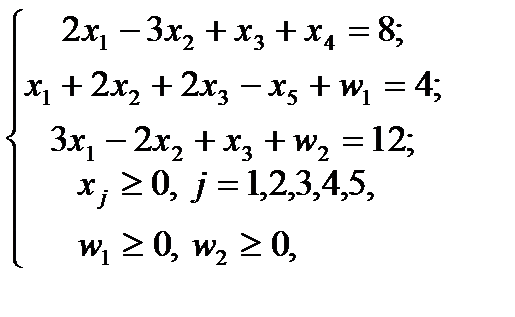
где w₁, w₂ – искусственные переменные. Система ограничений ВЗ в векторном виде имеет вид: A₁x₁+A₂x₂+A₃x₃+A₄x₄+A₅x₅+A₆w₁+A₇w₂=B, где вектора A_j , j=1,2,3,4,5 определяются также, как и выше, а 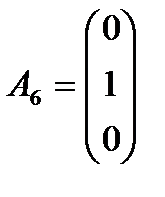и 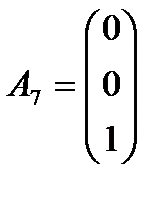. Таким образом, вектора A₄, A₆, A₇ образуют базис в R³ и им соответствуют базисные переменные (БП) – x₄, w₁, w₂. Все остальные переменные, а именно x₁, x₂, x₃, x₅ объявляются свободными (СП). Далее к ВЗ применяем обычный симплекс-метод. Как и раньше, см. §5.1, начальный опорный план получается, если присвоить свободным переменным значения, равные нулю. При этом базисные переменные принимают значения, равные числам в соответствующей строке столбца свободных коэффициентов В, то есть x₁=x₂=x₃=x₅=0¸ а x₄=8, w₁=4, w₂=12. Строим симплекс-таблицу, соответствующую начальному опорному плану:

СП БП .	x1	x2	x3	x5	B
x4		-3
w1				-1
w2		-2
F	-4		-3		-16

С этой таблицей проводим необходимые преобразования симплекс-метода, пока не получим оптимальную симплекс-таблицу или неразрешимость. В нашем случае, мы уже на втором шаге будем иметь такую симплекс-таблицу:

СП БП .	w1	x2	x3	w2	B
x4	-0,5	-3	-0,5	-0,5
x1	0,25		0,75	0,25
x5	-0,75	-2
F

Эта таблица будет оптимальной для ВЗ. При этом все искусственные переменные стали свободными и max F=0. Вычеркивая столбцы, соответствующие искусственным переменным и последнюю строку, и приписывая новую строку оценок с использованием исходной целевой функции Z(X), получим начальную симплекс-таблицу для исходной задачи ЛП:

СП БП .	x2	x3	B
x4	-3	-0,5
x1		0,75
x5	-2
Z	-2	2,75

Проанализировав последнюю таблицу, делаем вывод, что исходная задача ЛП не имеет решения в силу неограниченности целевой функции.