Образец индивидуального задания
ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
(линейные образы)
Задача 1
а) Найти параметрические уравнения прямой  , проходящей через точку
, проходящей через точку 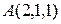 параллельно вектору
параллельно вектору 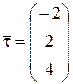 .
.
б) При каком значении параметра t точка 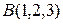 принадлежит этой прямой?
принадлежит этой прямой?
в) Принадлежит ли точка 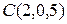 этой прямой?
этой прямой?
г) Построить данную прямую.
Задача 2
а) Составить параметрические уравнения прямой  , проходящей через точки
, проходящей через точки 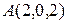 и
и 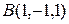 .
.
б) Используя параметр, найти координаты точек C и D, делящих отрезок 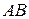 на три равные части.
на три равные части.
Задача 3
Построить плоскости и указать особенности их расположения:
а) 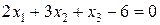 ;
;
б) 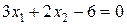 ;
;
в) 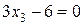 ;
;
г) 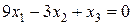 ;
;
д) 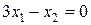 .
.
Задача 4
а) Составить уравнение плоскости  , которая проходит через точку
, которая проходит через точку 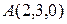 и имеет нормальный вектор
и имеет нормальный вектор 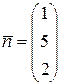 .
.
б) Принадлежит ли этой плоскости точка 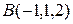 ?
?
Задача 5
Cоставить уравнение плоскости  , проходящей через три точки
, проходящей через три точки 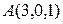 ,
, 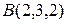 и
и 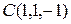 .
.
Задача 6
Составить уравнение плоскости  , проходящей через точку
, проходящей через точку 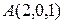 и прямую
и прямую 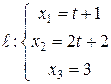 .
.
Задача 7
Составить уравнение плоскости  , проходящей через две параллельные прямые
, проходящей через две параллельные прямые 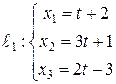 и
и 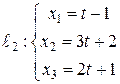 .
.
Задача 8
Составить уравнение плоскости  , проходящей через точки
, проходящей через точки 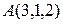 и
и 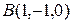 параллельно вектору
параллельно вектору 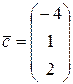 .
.
Задача 9
Составить уравнение плоскости  , проходящей через две точки
, проходящей через две точки 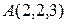 и
и 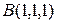 перпендикулярно плоскости
перпендикулярно плоскости 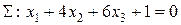 .
.
Задача 10
Составить уравнение плоскости  , проходящей через точку
, проходящей через точку 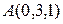 параллельно плоскости
параллельно плоскости 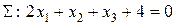 .
.
Задача 11
При каком значении параметра a плоскости 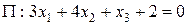 и
и 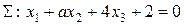 будут перпендикулярны?
будут перпендикулярны?
Задача 12
При каких значениях параметров a и b плоскости 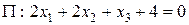 и
и 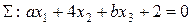 будут параллельны?
будут параллельны?
Задача 13
Найти точку пересечения прямой 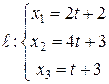 и плоскости
и плоскости 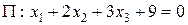 .
.
Задача 14
Найти угол между прямой 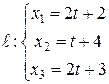 и плоскостью
и плоскостью 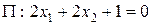 .
.
Задача 15
Найти проекцию точки 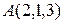 на плоскость
на плоскость 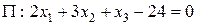 .
.
Задача 16
Найти проекцию точки 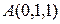 на прямую
на прямую 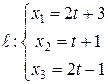 .
.
Задача 17
Дана прямая 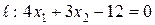 . Найти угловой коэффициент этой прямой и отрезок, отсекаемый ею на оси ординат. Построить эту прямую.
. Найти угловой коэффициент этой прямой и отрезок, отсекаемый ею на оси ординат. Построить эту прямую.
Задача 18
Дана прямая 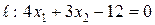 и точка
и точка 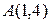 . Составить уравнение:
. Составить уравнение:
а) прямой 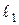 ,проходящей через точку A параллельно прямой
,проходящей через точку A параллельно прямой  ;
;
б) прямой 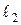 , проходящей через точку A перпендикулярно прямой
, проходящей через точку A перпендикулярно прямой  .
.
Задача 19
Даны вершины 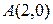 ,
, 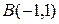 и
и 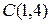 треугольника ABC. Составить:
треугольника ABC. Составить:
а) уравнение стороны BC;
б) уравнение высоты AH;
в) уравнение медианы AD.
Задача 20
Найти точку, симметричную точке 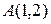 относительно прямой
относительно прямой 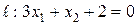 .
.
РЕШЕНИЕ ЗАДАЧ
Решение задачи 1
а) В данной задаче известны направляющий вектор 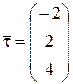 прямой
прямой  и точка
и точка 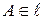 . Используя материал раздела «Параметрические уравнения прямой в
. Используя материал раздела «Параметрические уравнения прямой в 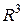 » (см., в частности, формулу (42) из лекции 10), получаем:
» (см., в частности, формулу (42) из лекции 10), получаем:
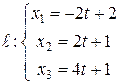 .
.
б) Подставляя в полученные параметрические уравнения прямой  вместо
вместо 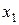 ,
, 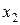 и
и 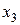 соответствующие координаты точки B, имеем:
соответствующие координаты точки B, имеем:
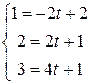
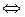
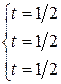 .
.
Таким образом, на прямой  точке B отвечает параметр
точке B отвечает параметр 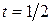 .
.
в) Подставим теперь в уравнения прямой  вместо
вместо 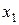 ,
, 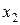 и
и 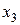 координаты точки C:
координаты точки C:
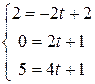
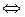
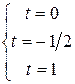 .
.
Таким образом, не существует единого числа t, при котором координаты точки C удовлетворяли бы всем уравнениям прямой  . Следовательно, точка C не принадлежит прямой
. Следовательно, точка C не принадлежит прямой  .
.
|
 , достаточно построить какие-нибудь две точки, принадлежащие этой прямой (в нашем случае, например, точки
, достаточно построить какие-нибудь две точки, принадлежащие этой прямой (в нашем случае, например, точки 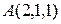 и
и 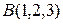 ) и затем соединить эти две точки при помощи линейки отрезком прямой:
) и затем соединить эти две точки при помощи линейки отрезком прямой: 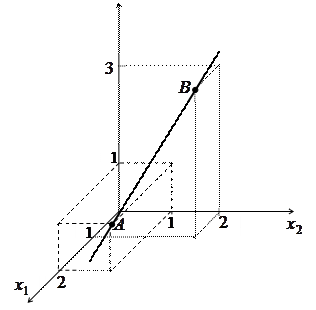 |
Решение задачи 2
а)Решение этой задачи повторяет решение примера 21 из лекции 10.
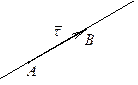 |
Направляющий вектор прямой  можно вычислить следующим образом:
можно вычислить следующим образом: 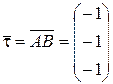
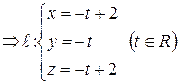 .
.
б)Сначало проведем одно общее рассуждение. Пусть 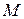 — точка на прямой
— точка на прямой  (заданной уравнениями (42) из лекции 10), соответствующая значению
(заданной уравнениями (42) из лекции 10), соответствующая значению 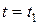 параметра, а
параметра, а 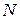 соответствует значению
соответствует значению 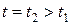 . Вычислим расстояние между этими точками. Имеем:
. Вычислим расстояние между этими точками. Имеем:
 |
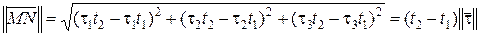 .
.
Таким образом, расстояние между двумя точками на  пропорционально разности соответствующих значений параметра.
пропорционально разности соответствующих значений параметра.
Вернемся теперь к нашей конкретной прямой. Ясно, что точке 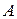 соответствует значение параметра
соответствует значение параметра 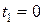 , а точке
, а точке 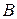 —
— 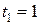 , причем
, причем 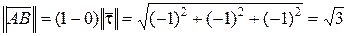 . Поэтому для точки
. Поэтому для точки 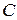 :
:
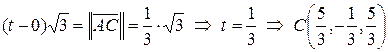 ,
,
а для точки 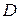 :
:
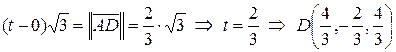 .
.
Решение задачи 3
а) Построим плоскость 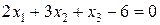 в отрезках на осях (это всегда можно сделать, если уравнение плоскости полное, то есть в нем присутствуют все три переменные и свободный член). Построение проводится так же, как и построение плоскости
в отрезках на осях (это всегда можно сделать, если уравнение плоскости полное, то есть в нем присутствуют все три переменные и свободный член). Построение проводится так же, как и построение плоскости 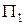 в примере 31 из лекции 12. Найдем точки пересечения
в примере 31 из лекции 12. Найдем точки пересечения 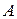 ,
, 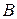 и
и 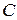 данной плоскости с координатными осями
данной плоскости с координатными осями 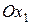 ,
, 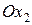 и
и 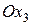 :
:
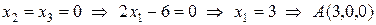 ,
,
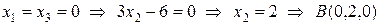 ,
,
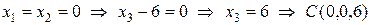 .
.
|
 , принадлежащий искомой плоскости:
, принадлежащий искомой плоскости: 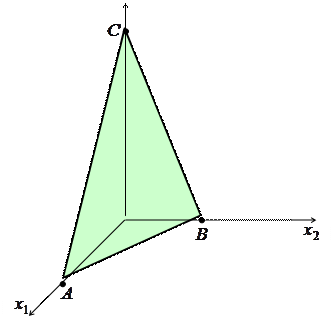 |
б) Построим плоскость 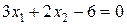 (см. также построение плоскости
(см. также построение плоскости  в примере 31 из лекции 12):
в примере 31 из лекции 12):
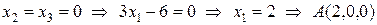 ,
,
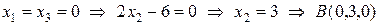 ,
,
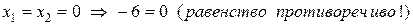 .
.
|
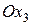 , то есть параллельна ей. Проведя из точек
, то есть параллельна ей. Проведя из точек 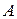 и
и 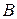 вверх равные отрезки
вверх равные отрезки 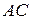 и
и 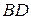 , параллельные оси
, параллельные оси 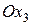 , а затем соединяя точки
, а затем соединяя точки 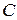 и
и 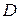 , получаем прямоугольник
, получаем прямоугольник 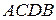 , принадлежащий искомой плоскости:
, принадлежащий искомой плоскости: 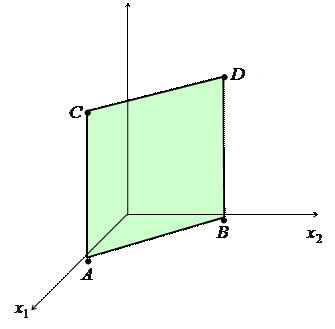 |
в) Построим плоскость 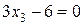 (см. также построение плоскости
(см. также построение плоскости  в примере 31 из лекции 12):
в примере 31 из лекции 12):
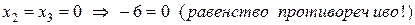 ,
,
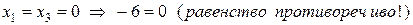 ,
,
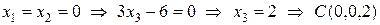 .
.
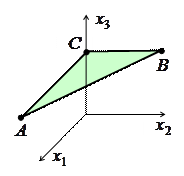
Полученные в первых двух случаях противоречия говорят о том, что наша плоскость не пересекается с осями 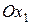 и
и 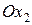 , то есть параллельна им. Проведя из точки
, то есть параллельна им. Проведя из точки 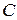 отрезки
отрезки 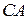 и
и 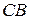 , параллельные осям
, параллельные осям 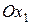 и
и 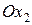 , а затем, соединяя точки
, а затем, соединяя точки 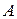 и
и 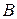 , получаем треугольник
, получаем треугольник 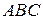 , принадлежащий искомой плоскости:
, принадлежащий искомой плоскости:
г) Построим плоскость 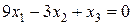 . Ясно, что эта плоскость проходит через начало координат
. Ясно, что эта плоскость проходит через начало координат 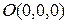 и не имеет других точек пересечения с осями координат. Найдем еще две точки, лежащие на данной плоскости:
и не имеет других точек пересечения с осями координат. Найдем еще две точки, лежащие на данной плоскости:
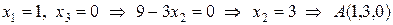 ,
,
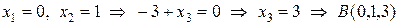 .
.
Соединяя точки 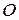 ,
, 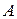 и
и 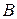 отрезками прямой, получаем треугольник
отрезками прямой, получаем треугольник 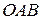 , принадлежащий искомой плоскости:
, принадлежащий искомой плоскости:
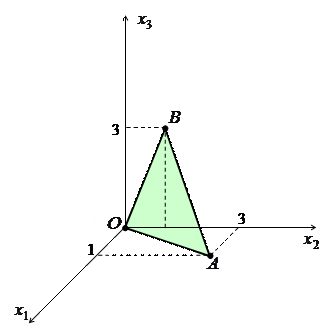
д) Построим плоскость 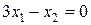 . Ясно, что эта плоскость проходит через начало координат
. Ясно, что эта плоскость проходит через начало координат 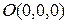 . Найдем еще две точки, лежащие на данной плоскости:
. Найдем еще две точки, лежащие на данной плоскости:
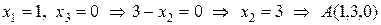 ,
,
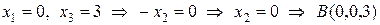 .
.
Соединяя точки 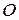 ,
, 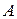 и
и 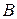 отрезками прямой, получаем треугольник
отрезками прямой, получаем треугольник 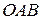 , принадлежащий искомой плоскости:
, принадлежащий искомой плоскости:
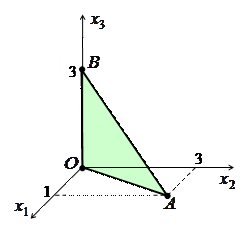
Ясно, что построенная плоскость содержит ось 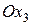 .
.
Решение задачи 4
а)
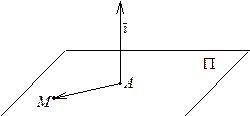 |
Решение данной задачи изложено в разделе «Построение плоскости по точке и нормальному вектору» в лекции 10. Применяя формулу (44) из той же лекции, получаем:
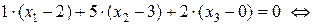
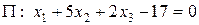 .
.
б)Для того, чтобы выяснить, принадлежит ли точка 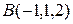 плоскости
плоскости  , нужно координаты этой точки подставить в полученное в предыдущем пункте уравнение этой плоскости:
, нужно координаты этой точки подставить в полученное в предыдущем пункте уравнение этой плоскости:
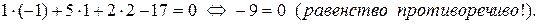
Следовательно, точка B не принадлежит плоскости  .
.
|
Введем текущую точку 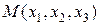 плоскости
плоскости  и вычислим векторы
и вычислим векторы 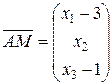 ,
, 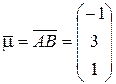 и
и 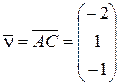 , принадлежащие данной плоскости:
, принадлежащие данной плоскости:
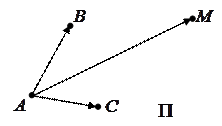 |

Ясно, что эти векторы линейно зависимы, следовательно 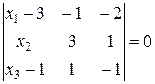 .
.
Раскрывая определитель и упрощая, получаем общее уравнение плоскости  :
:
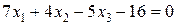 .
.
Заметим, что данную задачу можно решить, используя формулу (45) раздела «Уравнение плоскости по точке и двум векторам» (см. лекцию 10). Проделайте это самостоятельно!
Решение задачи 6
Анализируя параметрические уравнения заданной прямой  , приходим к выводу, что эта прямая проходит через точку с координатами
, приходим к выводу, что эта прямая проходит через точку с координатами 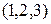 , которую мы обозначим через
, которую мы обозначим через 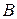 , и имеет направляющий вектор
, и имеет направляющий вектор 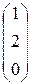 , который мы обозначим через
, который мы обозначим через 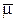 . Поместим начало этого вектора в точку
. Поместим начало этого вектора в точку 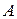 . Рассмотрим также вектор
. Рассмотрим также вектор 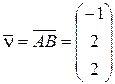 :
:
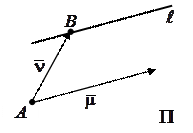 |

Запишем уравнение плоскости  по точке
по точке 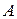 и двум векторам
и двум векторам 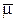 и
и 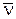 (см. формулу (45) из лекции 10):
(см. формулу (45) из лекции 10):
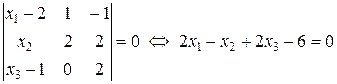 .
.
Решение задачи 7
Эта задача решается также, как пункт 3) примера 23 из лекции 10.
Из параметрических уравнений параллельных прямых 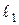 и
и 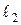 получаем:
получаем:
1) точку 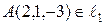 ;
;
2) точку 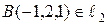 ;
;
3) общий направляющий вектор 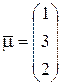 этих прямых.
этих прямых.
|
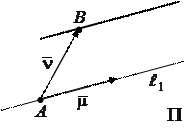
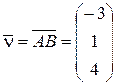 :
: 

Запишем уравнение плоскости  по точке
по точке 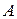 и двум векторам
и двум векторам 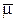 и
и 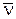 (см. формулу (45) из лекции 10):
(см. формулу (45) из лекции 10):
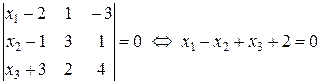 .
.
Решение задачи 8
Рассмотрим точку 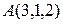 , а также векторы
, а также векторы 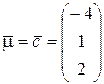 и
и 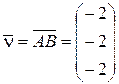 . Так же, как и в предыдущей задаче, записываем уравнение плоскости
. Так же, как и в предыдущей задаче, записываем уравнение плоскости  по точке
по точке 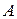 и двум векторам
и двум векторам 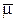 и
и 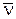 (см. формулу (45) из лекции 10):
(см. формулу (45) из лекции 10):
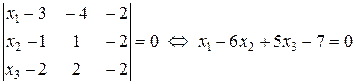 .
.
Решение задачи 9
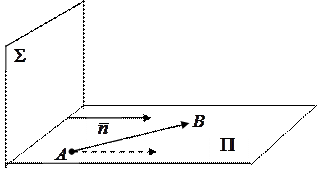
Из теоремы 19 (см. лекцию 11) вытекает, что 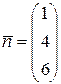 — нормальный вектор плоскости
— нормальный вектор плоскости 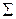 :
:
 |
|
Ясно, что вектор 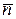 принадлежит плоскости
принадлежит плоскости  . Рассмотрев точку
. Рассмотрев точку 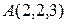 , а также векторы
, а также векторы 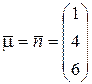 и
и 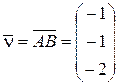 , получим, как и в предыдущих задачах, искомое уравнение плоскости
, получим, как и в предыдущих задачах, искомое уравнение плоскости  :
:
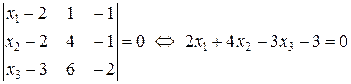 .
.
Решение задачи 10
Ясно, что нормальный вектор плоскости 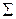 является одновременно нормальным вектором
является одновременно нормальным вектором 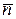 искомой плоскости
искомой плоскости  , то есть по теореме 19 (см. лекцию 11)
, то есть по теореме 19 (см. лекцию 11) 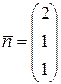 . Используя уравнение плоскости по точке
. Используя уравнение плоскости по точке 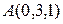 и нормальному вектору
и нормальному вектору 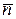 (см. формулу (44) из лекции 10), имеем:
(см. формулу (44) из лекции 10), имеем:
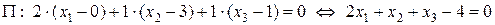 .
.
Чертеж к решению данной задачи рекомендуется построить самостоятельно.
Решение задачи 11
Из теоремы 19 лекции 11 вытекает, что 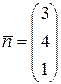 — нормальный вектор плоскости
— нормальный вектор плоскости  , а
, а 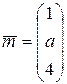 — нормальный вектор плоскости
— нормальный вектор плоскости 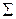 . Ясно, что две плоскости перпендикулярны тогда и только тогда, когда перпендикулярны их нормальные векторы. Итак:
. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда перпендикулярны их нормальные векторы. Итак:
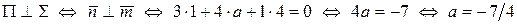 .
.
Решение задачи 12
Из теоремы 19 лекции 11 вытекает, что 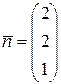 — нормальный вектор плоскости
— нормальный вектор плоскости  , а
, а 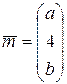 — нормальный вектор плоскости
— нормальный вектор плоскости 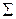 . Ясно, что две плоскости параллельны тогда и только тогда, когда коллинеарны их нормальные векторы. Итак:
. Ясно, что две плоскости параллельны тогда и только тогда, когда коллинеарны их нормальные векторы. Итак:
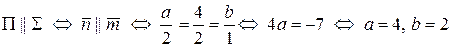 .
.
Решение задачи 13
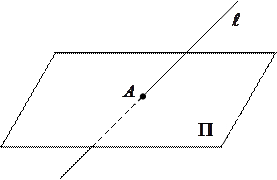
Перед решением этой задачи рекомендуется изучить теорему 20 и ее доказательство (см. лекцию 11).
Для нахождения общей точки прямой  и плоскости
и плоскости  нужно решить систему уравнений, составленную из параметрических уравнений прямой
нужно решить систему уравнений, составленную из параметрических уравнений прямой  и уравнения плоскости
и уравнения плоскости  :
:
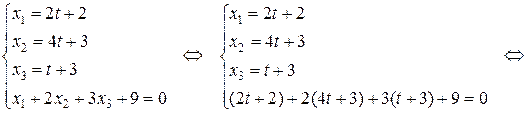
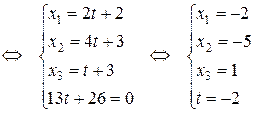 .
.
Таким образом, точка 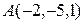 есть искомая точка пересечения прямой и плоскости.
есть искомая точка пересечения прямой и плоскости.
Решение задачи 14
Рассмотрим векторы 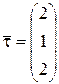 (направляющий вектор прямой
(направляющий вектор прямой  ) и
) и 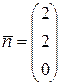 (нормальный вектор плоскости
(нормальный вектор плоскости  ):
):
 |
Ясно, что 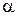 — угол между
— угол между  и
и  . Так как
. Так как 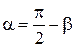 , где
, где 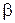 — угол между векторами
— угол между векторами 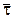 и
и 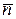 , то
, то
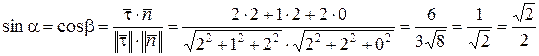 .
.
Следовательно, 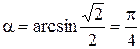 .
.
Решение задачи 15
Найдем точку 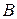 , являющуюся проекцией точки
, являющуюся проекцией точки 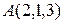 на плоскость
на плоскость 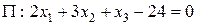 .
.
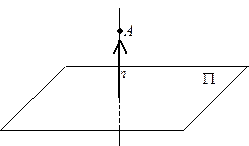 |
1) Запишем уравнение прямой 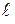 , проходящей через точку A перпендикулярно плоскости
, проходящей через точку A перпендикулярно плоскости  . Так как в качестве направляющего вектора
. Так как в качестве направляющего вектора 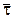 прямой
прямой 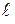 можно взять нормальный вектор плоскости
можно взять нормальный вектор плоскости  , который в силу теоремы 19 из лекции 11 равен
, который в силу теоремы 19 из лекции 11 равен
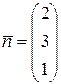 , то параметрические уравнения
, то параметрические уравнения 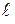 имеют вид:
имеют вид: 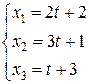 .
.
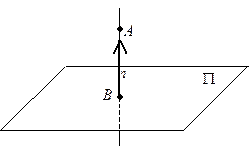 |
2) Найдем точку пересечения 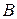 прямой
прямой 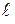 и плоскости
и плоскости  . Так же, как и в доказательстве теоремы 20 из лекции 11, решим систему уравнений:
. Так же, как и в доказательстве теоремы 20 из лекции 11, решим систему уравнений:
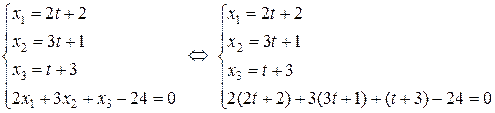 .
.
Таким образом, 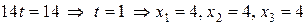 То есть,
То есть, 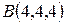 — проекция точки
— проекция точки 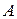 на плоскость
на плоскость  .
.
Решение задачи 16
Найдем проекцию 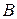 точки
точки 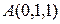 на прямую
на прямую 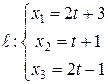 .
.
 |
1) Запишем уравнение плоскости  , проходящей через точку A перпендикулярно прямой
, проходящей через точку A перпендикулярно прямой 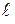 . Так как в качестве нормального вектора плоскости
. Так как в качестве нормального вектора плоскости  можно взять направляющий вектор прямой
можно взять направляющий вектор прямой 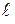 , который равен
, который равен 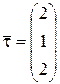 , то
, то 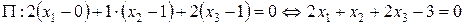 (см. формулу (44) из лекции 10).
(см. формулу (44) из лекции 10).
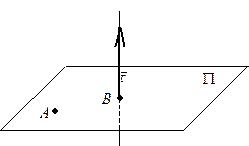 |
2) Найдем точку пересечения 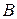 прямой
прямой 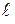 и плоскости
и плоскости  . Решим систему уравнений:
. Решим систему уравнений:
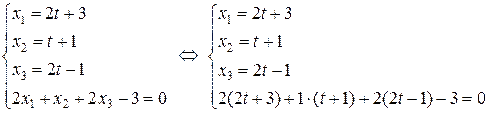 .
.
Получаем: 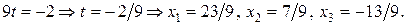 То есть точка
То есть точка 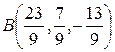 — проекция точки
— проекция точки 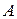 на прямую
на прямую  .
.
Решение задачи 17
До решения этой задачи рекомендуется изучить раздел «Уравнения прямой в 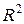 » из лекции 12.
» из лекции 12.
Угловой коэффициент прямой в 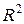 находится разрешением уравнения этой прямой относительно зависимой переменной
находится разрешением уравнения этой прямой относительно зависимой переменной 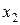 :
:
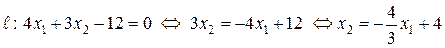 .
.
Угловой коэффициент 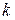 — это полученный коэффициент при
— это полученный коэффициент при 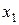 , то есть
, то есть 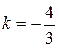 . Отрезок, отсекаемый прямой на оси
. Отрезок, отсекаемый прямой на оси 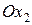 , получаем, подставив в наше уравнение
, получаем, подставив в наше уравнение 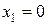 . Получаем
. Получаем 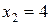 , то есть
, то есть 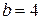 .
.
Построим прямую  по двум принадлежащим ей точкам. Одну точку мы уже нашли — это точка
по двум принадлежащим ей точкам. Одну точку мы уже нашли — это точка 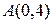 . Вторую точку лучше всего находить, подставив в уравнение
. Вторую точку лучше всего находить, подставив в уравнение 
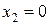 . Получаем
. Получаем 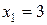 и точку
и точку 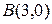 . Точки
. Точки 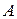 и
и 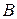 находятся на координатных осях, поэтому данное построение называется построением прямой в отрезках на осях:
находятся на координатных осях, поэтому данное построение называется построением прямой в отрезках на осях:
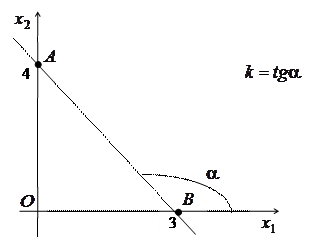 |
Решение задачи 18
Начнем с нахождения углового коэффициента прямой  . Он уже найден в предыдущей задаче:
. Он уже найден в предыдущей задаче: 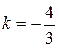 .
.
а)Так как 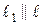 , а угловой коэффициент равен тангенсу угла наклона прямой к оси
, а угловой коэффициент равен тангенсу угла наклона прямой к оси 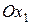 , то угловые коэффициенты этих прямых совпадают. Следовательно, угловой коэффициент искомой прямой
, то угловые коэффициенты этих прямых совпадают. Следовательно, угловой коэффициент искомой прямой 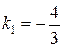 . Воспользуемся формулой (47) из лекции 12, то есть уравнением прямой в
. Воспользуемся формулой (47) из лекции 12, то есть уравнением прямой в 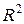 , проходящей через точку
, проходящей через точку 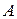 с угловым коэффициентом
с угловым коэффициентом 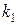 :
:
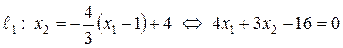 .
.
б)Пусть 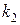 — угловой коэффициент прямой
— угловой коэффициент прямой 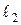 . Воспользуемся условием перпендикулярности двух прямых в
. Воспользуемся условием перпендикулярности двух прямых в 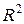 (см. формулу (52) из лекции 12):
(см. формулу (52) из лекции 12):
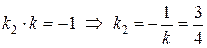 .
.
Опять применяем формулу (47):
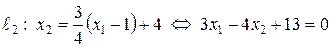 .
.
Решение задачи 19
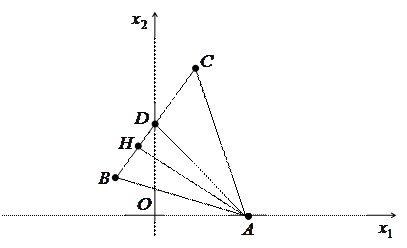
а) Для нахождения уравнения стороны BC применим формулу (50) из лекции 12 (уравнение прямой в 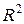 , проходящей через две точки):
, проходящей через две точки):
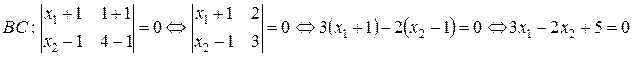 .
.
Из полученного уравнения находим угловой коэффициент прямой BC: 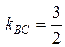 . б) Пользуясь условием ортогональности (52) из лекции 12, найдем угловой коэффициент
. б) Пользуясь условием ортогональности (52) из лекции 12, найдем угловой коэффициент 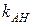 высоты
высоты 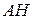 :
: 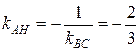 . Используя формулу (47) из лекции 12, запишем уравнение высоты
. Используя формулу (47) из лекции 12, запишем уравнение высоты 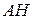 , проходящей через известную точку
, проходящей через известную точку 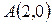 и имеющей известный угловой коэффициент
и имеющей известный угловой коэффициент 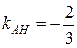 :
:
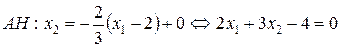 .
.
в)Так как 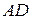 — медиана треугольника
— медиана треугольника 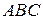 , то точка
, то точка 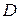 делит сторону
делит сторону 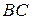 пополам, следовательно, координаты точки
пополам, следовательно, координаты точки 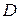 равны полусумме соответствующих координат точек
равны полусумме соответствующих координат точек 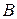 и
и 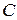 , то есть
, то есть 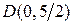 . В очередной раз воспользуемся формулой (50):
. В очередной раз воспользуемся формулой (50):
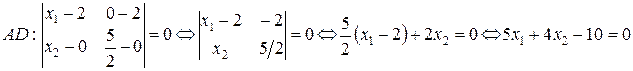 .
.
Решение задачи 20
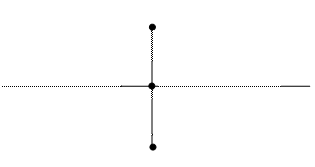 |
Напомним, что точка C симметрична точке A относительно прямой  , если она лежит на прямой
, если она лежит на прямой 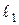 , перпендикулярной к
, перпендикулярной к  и проходящей через точку A, и расстояние от
и проходящей через точку A, и расстояние от 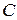 до
до  равно расстоянию от
равно расстоянию от 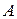 до
до  (см. рисунок). Прежде чем находить точку C, найдём точку B — проекцию
(см. рисунок). Прежде чем находить точку C, найдём точку B — проекцию 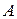 на
на  .Для этого составим уравнение проектирующей прямой
.Для этого составим уравнение проектирующей прямой 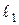 . Обозначим через
. Обозначим через 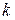 угловой коэффициент прямой
угловой коэффициент прямой  , а через
, а через 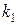 — прямой
— прямой 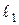 . Так как
. Так как 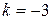 и
и 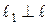 , то
, то 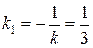 , а так как
, а так как 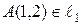 , то по формуле (47) имеем:
, то по формуле (47) имеем:
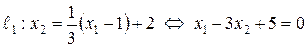 .
.
Далее, из того, что 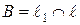 , вытекает, что координаты точки
, вытекает, что координаты точки 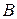 находятся из системы:
находятся из системы:
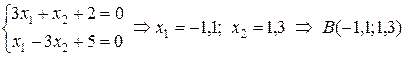 .
.
Теперь мы можем определить координаты точки 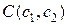 . Действительно, так как точка B делит отрезок AC пополам, то координаты точки B равны полусумме координат точек A и C, то есть:
. Действительно, так как точка B делит отрезок AC пополам, то координаты точки B равны полусумме координат точек A и C, то есть:
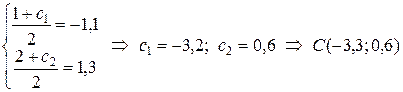 .
.
