Энергия гармонических колебания.
При гармонических колебаниях полная энергия системы сохраняется, но в различные моменты времени кинетическая и потенциальная энергии имеют разное значении, достигая максимального и минимального значений. Запишем формулы энергии для случая пружинного маятника.
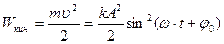 | кинетическая энергия |
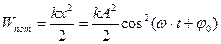 | потенциальная энергия |
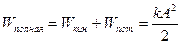 | полная энергии |
Из формул следует, что кинетическая и потенциальная энергии достигают максимумов дважды за период Т изменения смешения х и находятся в противофазах: когда кинетическая энергия максимальная, потенциальная равна нулю, и наоборот.
Тема 16. Вопрос 1.
Часть 1.
Затухающие колебания и вынужденные колебания.
При любом реальном движении всегда существуют силы трения или сопротивления. Это приводит к диссипации механической энергии. С течением времени механическая энергия колеблющейся системы переходит в тепловую, рассеиваясь в окружающую среду. Если механическую энергию не пополнять, то колебания будут затухать. Дифференциальное уравнение движения (II закон Ньютона) в этом случае принимает более сложный вид, чем в случае незатухающих колебаний, но самое главное, заранее неизвестно выражение для силы сопротивления. Мы рассмотрим частный случай, предполагая, что сила сопротивления пропорциональна скорости колеблющейся точки: 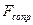 ~υ. В этом случае амплитуда смещения оказывается не постоянной, а убывающей по
~υ. В этом случае амплитуда смещения оказывается не постоянной, а убывающей по
экспоненциальному закону.
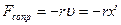 | сила сопротивления, r - коэффициент сопротивления среды |
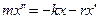 или или 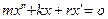 | II закон Ньютона при затухающих колебаниях |
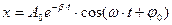 | смещение при затухающих колебаниях |
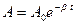 | амплитуда при затухающих колебаниях β - коэффициент затухания 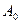 - амплитуда в начальный момент времени - амплитуда в начальный момент времени |
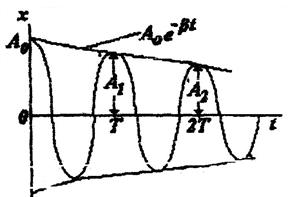 Если подставить в дифференциальное уравнение второго закона Ньютона х, х, х, получим уравнение, члены которого будут содержать синусы и косинусы. Объединяя члены с синусами и члены с косинусами, и учитывая, что уравнение должно выполняться при любых х, в-том числе при х = 0, получим два уравнения, из которых найдем коэффициент затухания β и циклическую частоту затухающих колебаний аx.
Если подставить в дифференциальное уравнение второго закона Ньютона х, х, х, получим уравнение, члены которого будут содержать синусы и косинусы. Объединяя члены с синусами и члены с косинусами, и учитывая, что уравнение должно выполняться при любых х, в-том числе при х = 0, получим два уравнения, из которых найдем коэффициент затухания β и циклическую частоту затухающих колебаний аx.
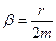 | коэффициент затухания, его величина тем больше чем больше коэффициент сопротивления седы r |
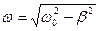 | циклическая частота затухающих колебаний |
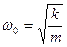 | циклическая частота собственных незатухающих колебаний, т. е колебаний, которые происходили бы в системе при отсутствии сил сопротивления |
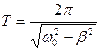 | период затухающих колебаний |
Тема 16. Вопрос 1.
Часть 2.
Если коэффициент затухания становится сравним с собственной частотой незатухающих колебаний 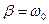 ,
, 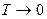 , и колебания переходят в периодическийрежим, при котором колебаний фактически нет, а наблюдается один «всплеск». При этом вся механическая энергия за одно колебание переходит в тепловую энергию. А периодический режим используют в стрелочных приборах или в аналитических весах, чтобы погасить ненужные колебания. Затухающие колебания характеризуют
, и колебания переходят в периодическийрежим, при котором колебаний фактически нет, а наблюдается один «всплеск». При этом вся механическая энергия за одно колебание переходит в тепловую энергию. А периодический режим используют в стрелочных приборах или в аналитических весах, чтобы погасить ненужные колебания. Затухающие колебания характеризуют
следующими величинами.
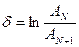 | логарифмический декремент затухания.Это натуральный логарифм отношения предыдущей амплитуды к последующей за время, равное периоду колебаний. |
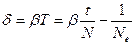 | связь между различными характеристиками затухающих колебаний T – период, N – полное число колебаний за время t, 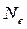 число колебаний за которое амплитуда убывает в е раз (е = 2,7… основание натуральных логарифмов) число колебаний за которое амплитуда убывает в е раз (е = 2,7… основание натуральных логарифмов) |
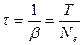 | время релаксации- это время, за которое амплитуда убывает в е раз. |
Коэффициент затухания - это величина, обратная времени релаксации, а логарифмический декремент затухания – величина, обратная числу колебаний, за которые амплитуда уменьшается в ераз. Например, пусть при некоторых колебаниях δ = 0,01, β = 100 1/с. Это означает, что за время 0,01 с амплитуда уменьшается в е раз и при этом совершается 100 колебаний.
Тема 16. Вопрос 2.
Вынужденные колебания.
Если на колебательную систему воздействовать внешней периодически изменяющейся силой 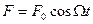 , то в системе возникают вынужденные колебания.
, то в системе возникают вынужденные колебания.
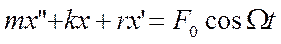 | Это II закон Ньютона дли системы, в которой действует возвращающая сила (кх), сила сопротивления (кυ) и внешняя вынуждающая сила, круговая частота изменения которой равна Ω, |
Решение этого дифференциального уравнения складывается из двух решений: общего решения для свободных затухающих колебаний и частного решения для вынужденных колебаний:
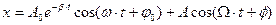 |
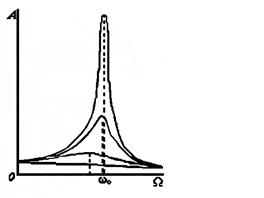
Вначале в течение некоторого времени в зависимости от сдвига фаз Ф, могут преобладать те или иные колебания. Это время называют временем релаксации. Но с течением времени собственные колебания затухают и в системе устанавливаются гармонические колебания, но не со своей частотой ω, а с частотой Ω, которую задает внешняя сила. Амплитуда вынужденных колебаний сложным образом зависит от массы системы, амплитуды внешней силы 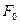 ,коэффициента затухания β собственной частоты ω и частоты изменения вынуждающей силы Ω. Если частота изменения внешней силы совпадает с собственной частотой колебаний системы Ω = ω, происходит очень резкое увеличение амплитуды колебаний. Это явление называют резонансом. Резонанс может быть как полезным, так и вредным. Если, например, двигатель плохо закреплен и «бьет», то при совпадении частот может быть разрушена опора. Известны случаи разрушения мостов под порывами ветра, разрушения самолетов. С другой стороны, на явлении резонанса основана вся прикладная акустика и радиотехника, аппараты, воспринимающие электрические и звуковые колебания. Резонанс является наиболее удобным методом измерения частоты колебаний.
,коэффициента затухания β собственной частоты ω и частоты изменения вынуждающей силы Ω. Если частота изменения внешней силы совпадает с собственной частотой колебаний системы Ω = ω, происходит очень резкое увеличение амплитуды колебаний. Это явление называют резонансом. Резонанс может быть как полезным, так и вредным. Если, например, двигатель плохо закреплен и «бьет», то при совпадении частот может быть разрушена опора. Известны случаи разрушения мостов под порывами ветра, разрушения самолетов. С другой стороны, на явлении резонанса основана вся прикладная акустика и радиотехника, аппараты, воспринимающие электрические и звуковые колебания. Резонанс является наиболее удобным методом измерения частоты колебаний.
Тема 17. Вопрос 1.
Волновые процессы.
Если в какой-либо упругой среде (твердой, жидкой, газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами, это колебание будет распространяться в среде от частицы к частице с некоторой скоростью. Процесс распространения колебаний в пространстве называется волной. При волновом процессе частицы не переносятся с волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные и поперечные волны. В продольной волне частицы колеблются вдоль направления распространения волны (звуковые волны). В поперечной волне частицы колеблются перпендикулярно направлению распространения волны (Волны на поверхности воды, электромагнитные волны).
Волны характеризуют следующими величинами.
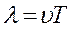 | длина волны - это: 1) расстояние, которое проходит волна за время, равное периоду колебаний T, или 2) это расстояние между соседними точками, колеблющимися в одинаковых фазах. |
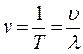 | v (Гц = 1/с) - частота колебаний - это число колебаний за единицу времени, υ - скорость волны (не путать со скоростью колебаний). |
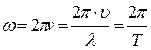 | ω (рад/с) круговая (циклическая частота) колебаний |
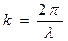 | волновое число |
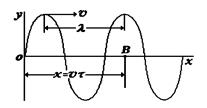 Получим уравнение простейшей плоской монохроматической бегущей волны. Волна называется плоской, когда на бесконечно малом интервале расстояний dx смещение y остается постоянным во всей своей плоскости. Монохроматической волной называют волну, в которой колебания происходят с одной частотой. Пусть в точке О происходят колебания. Представим себе, что это поверхность воды. В точку В колебания дойдут с задержкой во времени
Получим уравнение простейшей плоской монохроматической бегущей волны. Волна называется плоской, когда на бесконечно малом интервале расстояний dx смещение y остается постоянным во всей своей плоскости. Монохроматической волной называют волну, в которой колебания происходят с одной частотой. Пусть в точке О происходят колебания. Представим себе, что это поверхность воды. В точку В колебания дойдут с задержкой во времени 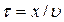
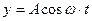 | уравнение колебаний в точке О |
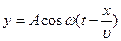 | уравнение колебаний в точке B. Это и есть уравнение волны, т.к. смещение является функцией не только времени t, но и расстояния х. |
Используя вышеприведенные формулы, уравнение волны можно записать в различной форме.
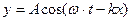 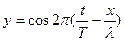 | уравнение плоской монохроматической волны |
Тема 17. Вопрос 2.
Стоячие волны.
При наложении двух встречных волн с одинаковыми периодами и амплитудами возникает колебательный процесс, который называют стоячей волной. Стоячая волна образуется при отражении волн от препятствий. Падающая (прямая) и отраженная (обратная) волны накладываются одна на другую и образуют стоячую волну. Стоячую волну можно наблюдать, если привязать один конец веревки, например, к стене, а свободный конец быстро перемещать вверх-вниз. Получим уравнение стоячей волны.
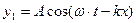 | уравнение прямой волны |
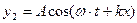 | уравнение обратной волны |
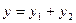 | смещение в образующейся стоячей волне |
Подставляя 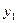 и
и 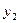 после тригонометрических преобразований, получим
после тригонометрических преобразований, получим
выражение для смещения точек в стоячей волне.
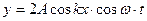 | уравнение стоячей волны |
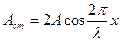 | амплитуда стоячей волныλ — длина бегущей волны |
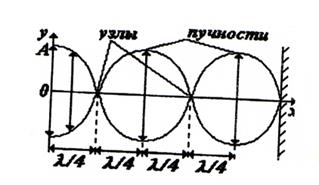
В стоячей волне каждая точка совершает вертикальные колебания с различными амплитудами (в бегущей волне, о которой говорилось ранее, все точки колеблются с одинаковыми амплитудами). Если точки находятся на расстояниях
х = λ/4, З λ /4, 5 λ /4,..,она не совершает колебаний, такие точки называются
узлами. Амплитуда точек, находящихся на расстояниях х = 0,2 λ/4, 4 λ /4,..., оказывается максимальной и равной 2 λ. Эти положения точек в стоячей волне называются пучностями.
Тема 18. Вопрос 1.
Электромагнитная волна - это распространяющиеся в пространстве электрическое и магнитное поля.
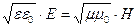 | связь между напряженностью электрического поля и напряженностью магнитного поля электромагнитной волны |
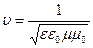 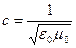 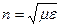 | υ - скорость электромагнитной волны в середе с - скорость электромагнитной волны в вакуумеп - показатель преломления вещества μ ≡ 1 - магнитная проницаемость для большинства веществ близка к единице |
Тема 18. Вопрос 2.
Если записать уравнения теории Максвелла в дифференциальной форме для простейшего случая, когда электрическое и магнитное поле распространяется в однородном диэлектрике (вакуум) только в одном направлении х, т.е напряженности Е и H=f(x,t), можно получить волновое уравнение для E и аналогичное для H. Решениями этих уравнений являются:
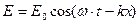 | уравнения плоской бегущей монохроматической волны |
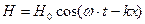 |
Из теории Максвелла следует, что электромагнитные волны являются поперечными: векторы Е и H направлены всегда перпендикулярно х - направлению их распространения.
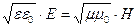 | связь между напряженностью электрического поля и напряженностью магнитного поля электромагнитной волны |
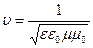 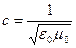 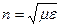 | υ - скорость электромагнитной волны в середе с - скорость электромагнитной волны в вакуумеп - показатель преломления вещества μ ≡ 1 - магнитная проницаемость для большинства веществ близка к единице |
Тема 18. Вопрос 3.
